神经网络的前向传播与反向传播及用numpy搭建神经网络
文章目录
- 前言
- 一.全连接神经网络
-
- 1.1从单个感知机到神经网络
- 1.2DNN的基本结构
- 1.3前向传播算法
- 1.4梯度下降算法
- 1.5反向传播算法
- 1.6激活函数
-
- 1.relu函数
- 2.sigmoid函数
- 3.tanh函数
- 4.softmax函数
- 二.卷积神经网络
-
- 2.1卷积神经网络的基本结构
-
- 1.卷积
- 2.池化
- 2.2卷积神经网络的前向传播
-
- 1.卷积层
- 2.池化层
- 3.全连接层
- 2.3卷积神经网络的反向传播
-
- 1.已知池化层的 δ l δ^l δl,推到上一层的 δ l − 1 δ^{l-1} δl−1
- 2已知卷积层的 δ l δ^{l} δl,求上一层的 δ l − 1 δ^{l-1} δl−1
- 三.用numpy搭建神经网络
-
- 3.1DNN的numpy实现:
-
- 1.定义激活函数以及激活函数的导数:
- 2参数w,b初始化:
- 3.定义前向传播函数:
- 4.计算损失:
- 5.定义反向传播函数:
- 6.参数更新:
- 7.模型定义:
- 3.2 CNN的numpy实现:
- 1.卷积层的前向传播:
- 2.池化层的前向传播:
- 3.卷积层的反向传播:
- 4.池化层的反向传播:
- 四.参考资料
前言
近期学习了神经网络前向传播和反向传播的数学原理,希望通过写下这篇文章进一步巩固自己对近期学习知识的理解,以及帮助同样有相同需求的人。若有错误,望指出。
一.全连接神经网络
1.1从单个感知机到神经网络
感知机是由多个输入和一个输出的模型。输入与权重相乘再求和,得到一个线性关系的结果:
z = ∑ i = 1 m w i x i + b z = \sum_{i=1}^mw_ix_i+b z=i=1∑mwixi+b
得到的线性结果再通过激活函数:
s i g n ( z ) = { 1 z > = 0 − 1 z < 0 sign(z) = \begin{cases}1& z>=0\\-1&z<0\end{cases} sign(z)={1−1z>=0z<0
最后得到的输出只能应用与二元分类,并且无法学习更复杂非线性模型,这是单个感知机的缺陷。
因此在单个感知机的基础上,通过增加单层感知机的个数以及感知机的层数,构成了人工神经网络(ANN),因此,人工神经网络也被称作多层感知机(MLP),如图2。
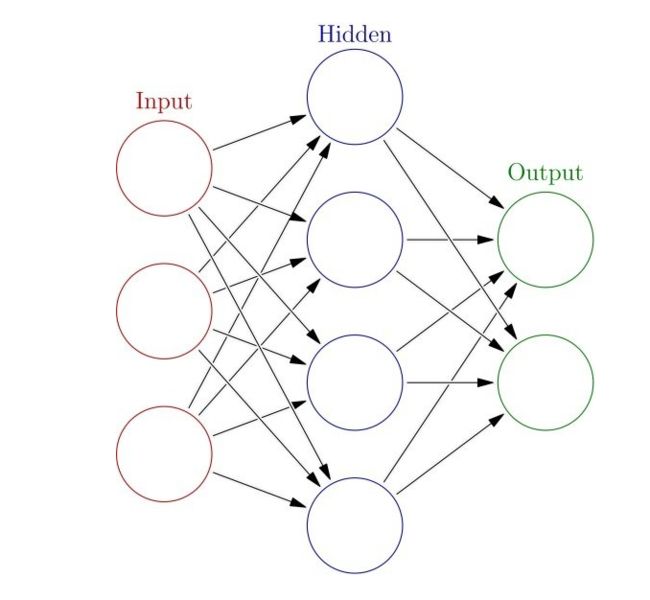
1.2DNN的基本结构
神经网络之所以被称作网络,是因为它们通常是用许多不同函数复合在一起来表示。该模型与一个有向无环图相关联,而图描述了函数是如何复合在一起的。例如,我们有三个函数 f ( 1 ) ( x ) f^{(1)}(x) f(1)(x), f ( 2 ) ( x ) f^{(2)}(x) f(2)(x), f ( 3 ) ( x ) f^{(3)}(x) f(3)(x), f ( 4 ) ( x ) f^{(4)}(x) f(4)(x), f ( 5 ) ( x ) f^{(5)}(x) f(5)(x), f ( 6 ) ( x ) f^{(6)}(x) f(6)(x)连接在一个链上以形成 f ( x ) = f ( 1 ) ( f ( 2 ) ( f ( 3 ) ( f ( 4 ) ( f ( 5 ) ( f ( 6 ) ( x ) ) ) ) ) ) f(x) = f^{(1)}(f^{(2)}(f^{(3)}(f^{(4)}(f^{(5)}(f^{(6)}(x)))))) f(x)=f(1)(f(2)(f(3)(f(4)(f(5)(f(6)(x))))))。 在这种情况下, f ( 1 ) ( x ) f^{(1)}(x) f(1)(x)被称为网络的第一层,也就是输入层, f ( 2 ) ( x ) f^{(2)}(x) f(2)(x)到 f ( 5 ) ( x ) f^{(5)}(x) f(5)(x)被称为隐藏层, f ( 6 ) ( x ) f^{(6)}(x) f(6)(x)被称为输出层。也就是说,DNN按照层的位置来划分的话,可以分为3类:输入层,隐藏层,输出层。一般来说,输入层为网络的第一层,输出层为最后一层。如图3为DNN结构样例:

1.3前向传播算法
前向传播其实就是向神经网络中输入X得到Y的过程。也就是可以把神经网络写成 f ( X ) = Y f(X) = Y f(X)=Y函数,而函数的系数就是神经网络训练的参数W。接下来我们就从数学的角度来推导前向传播的过程

记 w j k l w_{jk}^l wjkl为第 l l l-1层的第 j j j个神经元到第 l l l层第 k k k个神经元的权重, b j l b_j^l bjl为第 l l l层第 j j j个神经元的偏置, a j l a_j^l ajl为第 l l l层第 j j j个神经元的输出值, σ ( x ) σ(x) σ(x)为激活函数,所以
{ a 1 ( 2 ) = σ ( ∑ i = 1 3 w 1 i 2 x i + b 1 2 ) a 2 ( 2 ) = σ ( ∑ i = 1 3 w 2 i 2 x i + b 2 2 ) a 3 ( 2 ) = σ ( ∑ i = 1 3 w 3 i 2 x i + b 3 2 ) \begin{cases}a_1^{(2)} =σ(\sum_{i=1}^3w_{1i}^2x_i+b_1^2) \\a_2^{(2)} =σ(\sum_{i=1}^3w_{2i}^2x_i+b_2^2)\\a_3^{(2)} =σ(\sum_{i=1}^3w_{3i}^2x_i+b_3^2) \end{cases} ⎩⎪⎨⎪⎧a1(2)=σ(∑i=13w1i2xi+b12)a2(2)=σ(∑i=13w2i2xi+b22)a3(2)=σ(∑i=13w3i2xi+b32)
写成矩阵形式:
a l = σ ( w l x l − 1 + b l ) a^l = σ(w^lx^{l-1}+b^l) al=σ(wlxl−1+bl)
记 z l = w l x l − 1 = b l z^l = w^lx^{l-1}=b^l zl=wlxl−1=bl,则 a l = σ ( z ) a^l = σ(z) al=σ(z)。
利用式子 a l = σ ( z ) a^l = σ(z) al=σ(z)一层层计算,就能根据 X X X得到相应的输出 Y Y Y。
1.4梯度下降算法
梯度下降算法是神经网络进行反向传播的基础,因此,在介绍反向传播算法之前,我们先介绍一下什么是梯度下降算法以及梯度下降算法的数学原理。
1.梯度下降算法的解释:
假设甲现在处在一个山沟当中,如图5所示。在山沟的最低点有一个宝藏,甲希望能够找到这个宝藏。那么甲如何才能够沿着正确的方向找到宝藏呢?由于宝藏在山沟的最低点,所以甲会按着一定的步伐沿着下坡的方向前进,于是就有了①→②→③→④→⑤,由于甲的步伐过大,所以直接跨过了最低点,甲于是沿着另一个坡下坡的方向前进,于是有了⑤→⑥,最终到达了最低点。
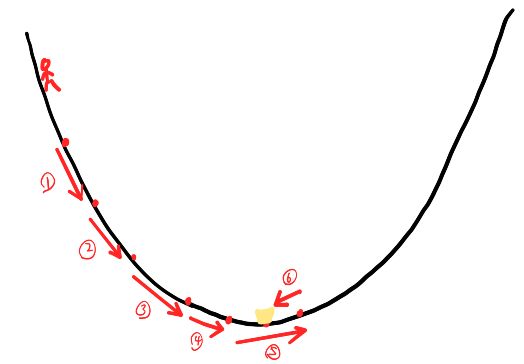
2.梯度下降的数学解释:
首先我们引入梯度下降算法的公式:
J m i n ( ω , θ ) = J m i n ( ω , θ ) − α ∗ ▽ J ( ω , θ ) J_{min}(ω,θ) = J_{min}(ω,θ)-α*▽J(ω,θ) Jmin(ω,θ)=Jmin(ω,θ)−α∗▽J(ω,θ)
假设我们有一个目标函数 J ( ω , θ ) J(ω,θ) J(ω,θ),我们希望我们有一种算法,能够找到目标函数的最低值,有什么办法能够帮助我们找到呢?参考甲寻宝的过程,我们知道沿着下坡的方向,就能找到最低值。而在函数中,上坡与下坡代表着函数在该点梯度的方向与梯度的反方向。在多变量函数中,梯度是一个向量,用符号▽表示,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向,反方向就是下降最快的方向。 针对目标函数 J ( ω , θ ) J(ω,θ) J(ω,θ),我们来求解他的梯度,其实就是求个 J J J关于 ω , θ ω,θ ω,θ的偏微分。
▽ J ( ω , θ ) = ( ∂ J ∂ ω , ∂ J ∂ θ ) ▽J(ω,θ)= ({{∂J}\over∂ω},{∂J\over∂θ}) ▽J(ω,θ)=(∂ω∂J,∂θ∂J)
在知道我们应该沿着哪个方向下坡时,我们又会面临另一个问题,我们每次迈出的步伐是多少,于是我们引入 α α α来表示步伐, α α α也称为学习率。如果 α α α设置过大,会导致我们直接迈过最低点,就如第⑤步一样;如果我们 α α α设置过小,会导致我们走了很久也没有到达最低点,因此设置合理的 α α α值很重要。
有了梯度 ▽ J ▽J ▽J和学习率 α α α我们就能够通过多次迭代,找到 J m i n ( ω , θ ) J_{min}(ω,θ) Jmin(ω,θ)
1.5反向传播算法
有了对梯度下降算法的了解,我们现在开始去看看神经网络是如何通过反向传播来更新参数的。
在介绍反向传播之前,我们引入损失函数 J ( w , x , b , y ) J(w,x,b,y) J(w,x,b,y),用来描述预测值与真实值之间的差异。
在反向传播的过程中,我们需要计算 ∂ J ∂ w , ∂ J ∂ b {∂J\over∂w},{∂J\over∂b} ∂w∂J,∂b∂J来对参数 w , b w,b w,b进行更新。在这里我们假设我们的误差函数为均方误差:
J ( w , x , b , y ) = 1 2 ∣ ∣ a L − y ∣ ∣ 2 2 J(w,x,b,y) = {1\over2}||a^L-y||_2^2 J(w,x,b,y)=21∣∣aL−y∣∣22
其中 a L a^L aL为网络第 L L L层的输出, y y y为真实值, ∣ ∣ X ∣ ∣ 2 ||X||_2 ∣∣X∣∣2表示 L 2 L2 L2范数
我们又知道 a L a^L aL和 w , b w,b w,b满足:
a L = σ ( w L a L − 1 + b L ) a^L = σ(w^La^{L-1}+b^L) aL=σ(wLaL−1+bL)
所以我们可以把损失函数写成:
J ( w , x , b , y ) = 1 2 ∣ ∣ σ ( w L a L − 1 + b L ) − y ∣ ∣ 2 2 J(w,x,b,y) = {1\over2}||σ(w^La^{L-1}+b^L)-y||_2^2 J(w,x,b,y)=21∣∣σ(wLaL−1+bL)−y∣∣22
于是损失函数 J J J关于 w , b w,b w,b的梯度为:
∂ J ( w , x , b , y ) ∂ w L = ( a L − y ) ⋅ σ ′ ( z L ) ( a L − 1 ) T {∂J(w,x,b,y)\over∂w^L} = (a^L-y)·σ'(z^L)(a^{L-1})^T ∂wL∂J(w,x,b,y)=(aL−y)⋅σ′(zL)(aL−1)T
∂ J ( w , x , b , y ) ∂ b L = ( a L − y ) ⋅ σ ′ ( z L ) {∂J(w,x,b,y)\over∂b^L} = (a^L-y)·σ'(z^L) ∂bL∂J(w,x,b,y)=(aL−y)⋅σ′(zL)
注: ⋅ · ⋅表示两向量的内积,例:
A = ( a 1 , a 2 , . . . a n ) , B = ( b 1 , b 2 , . . . b n ) A=(a_1,a_2,...a_n), B=(b_1,b_2,...b_n) A=(a1,a2,...an),B=(b1,b2,...bn)
A ⋅ B = ( a 1 b 1 , a 2 b 2 , . . . a n b n ) A·B = (a_1b_1,a_2b_2,...a_nb_n) A⋅B=(a1b1,a2b2,...anbn)
在求解 ∂ J ( w , x , b , y ) ∂ w L , ∂ J ( w , x , b , y ) ∂ b L {∂J(w,x,b,y)\over∂w^L},{∂J(w,x,b,y)\over∂b^L} ∂wL∂J(w,x,b,y),∂bL∂J(w,x,b,y)时,我们根据微分的链式法则,可以分解为 ∂ J ( w , x , b , y ) ∂ a L ∂ a L ∂ z L ∂ z L ∂ w L , ∂ J ( w , x , b , y ) ∂ a L ∂ a L ∂ z L ∂ z L ∂ b L {∂J(w,x,b,y)\over∂a^L}{∂a^L\over∂z^L}{∂z^L\over∂w^L},{∂J(w,x,b,y)\over∂a^L}{∂a^L\over∂z^L}{∂z^L\over∂b^L} ∂aL∂J(w,x,b,y)∂zL∂aL∂wL∂zL,∂aL∂J(w,x,b,y)∂zL∂aL∂bL∂zL
我们可以先求解出公共部分 ∂ J ( w , x , b , y ) ∂ a L ∂ a L ∂ z L {∂J(w,x,b,y)\over∂a^L}{∂a^L\over∂z^L} ∂aL∂J(w,x,b,y)∂zL∂aL
记为:
δ L = ∂ J ( w , x , b , y ) ∂ a L ∂ a L ∂ z L = ( a L − y ) ⋅ σ ′ ( z L ) δ^L = {∂J(w,x,b,y)\over∂a^L}{∂a^L\over∂z^L}=(a^L-y)·σ'(z^L) δL=∂aL∂J(w,x,b,y)∂zL∂aL=(aL−y)⋅σ′(zL)
对于第 l l l层的 w l w^l wl和 b l b^l bl, δ δ δ又为多少呢,根据链式求导法则,我们可以知道:
δ l = ∂ J ( w , x , b , y ) ∂ a L ∂ a L ∂ z l = ( ∂ z L ∂ z L − 1 ∂ z L − 1 ∂ z L − 2 . . . ∂ z l + 1 ∂ z l ) T ∂ J ( w , x , b , y ) ∂ z L δ^l = {∂J(w,x,b,y)\over∂a^L}{∂a^L\over∂z^l}=({∂z^L\over∂z^{L-1}}{∂z^{L-1}\over∂z^{L-2}}...{∂z^{l +1}\over∂z^{l}})^T{∂J(w,x,b,y)\over∂z^L} δl=∂aL∂J(w,x,b,y)∂zl∂aL=(∂zL−1∂zL∂zL−2∂zL−1...∂zl∂zl+1)T∂zL∂J(w,x,b,y)
我们再根据链式求导法则:
∂ J ( w , x , b , y ) ∂ δ l = ∂ J ( w , x , b , y ) ∂ δ l + 1 δ l + 1 δ l {∂J(w,x,b,y)\over∂δ^{l}} = {∂J(w,x,b,y)\over∂δ^{l+1}}{δ^{l+1}\overδ^{l}} ∂δl∂J(w,x,b,y)=∂δl+1∂J(w,x,b,y)δlδl+1
因此我们根据上一层 δ l + 1 δ^{l+1} δl+1的梯度来求解 δ l δ^{l} δl的梯度,这也是反向传播的特点,从 L L L层一步一步求解到第 1 1 1层。
又因为 z l = w l a l − 1 + b l z^l = w^la^{l-1}+b^l zl=wlal−1+bl,所以我们可以计算出第 l l l层 w , b w,b w,b的梯度值:
∂ J ( w , x , b , y ) ∂ w l = δ l ( a l − 1 ) T {∂J(w,x,b,y)\over∂w^l} = δ^l(a^{l-1})^T ∂wl∂J(w,x,b,y)=δl(al−1)T
∂ J ( w , x , b , y ) ∂ b l = δ l {∂J(w,x,b,y)\over∂b^l} = δ^l ∂bl∂J(w,x,b,y)=δl
到此,我们就求解出了 w w w和 b b b的梯度,然后我们用梯度下降算法,来对参数 w , b w,b w,b进行更新:
w l = w l − α ∗ ∂ J ( w , x , b , y ) ∂ w l w^l=w^l-α*{∂J(w,x,b,y)\over∂w^l} wl=wl−α∗∂wl∂J(w,x,b,y)
b l = b l − α ∗ ∂ J ( w , x , b , y ) ∂ b l b^l=b^l-α*{∂J(w,x,b,y)\over∂b^l} bl=bl−α∗∂bl∂J(w,x,b,y)
如此一来,我们就实现了神经网络的反向传播。
1.6激活函数
我们知道,如果没有激活函数,那么整个神经网络都是线性模型,就算网络有多深,其拟合能力和logistics回归差不多,而在添加了激活函数后,模型才有线性变成了非线性,因此,激活函数在神经网络中起了十分重要的作用。在这一部分,我讲介绍一些激活函数,以及这些激活函数的作用。
1.relu函数
relu全称为整流线性单元(rectified linear unit)其函数表达式为: g ( z ) = m a x ( 0 , z ) g(z) = max(0,z) g(z)=max(0,z),其函数如图6所示:

ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变,这种操作被成为单侧抑制。(也就是说:在输入是负值的情况下,它会输出0,那么神经元就不会被激活。这意味着同一时间只有部分神经元会被激活,从而使得网络很稀疏,进而对计算来说是非常有效率的。)正因为有了这单侧抑制,才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中,当模型增加N层之后,理论上ReLU神经元的激活率将降低2的N次方倍。
其优点有:
1.没有饱和区,不存在梯度消失问题。
2.没有复杂的指数运算,计算简单、效率提高。
3.实际收敛速度较快,比 Sigmoid/tanh 快很多。
4.比 Sigmoid 更符合生物学神经激活机制。
relu函数的一些变种:
(1).Leaky ReLU:带泄露线性整流函数(Leaky ReLU)的梯度为一个常数 λ λ λ,通常取0.01。在输入值为正的时候,带泄露线性整流函数和普通斜坡函数保持一致。函数为:
g ( z ) = { z z > = 0 λ z z < 0 g(z) = \begin{cases}z& z>=0\\λz&z<0\end{cases} g(z)={zλzz>=0z<0
(2).绝对值整流:固定 a i = − 1 a_i=-1 ai=−1来得到 g ( z ) = g ( z , a ) i = m a x ( 0. z i ) + a i m i n ( 0 , z i ) g(z)=g(z,a)_i=max(0.z_i)+a_imin(0,z_i) g(z)=g(z,a)i=max(0.zi)+aimin(0,zi),它一般用于图像中的对象识别,其中寻找输入照明极性反转下不变的特性是有意义的。
2.sigmoid函数
sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点:
优点:平滑、易于求导。
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
其函数式为:
g ( z ) = 1 ( 1 + e − z ) g(z) = {1\over(1+e^{-z})} g(z)=(1+e−z)1
函数图像如下图7

3.tanh函数
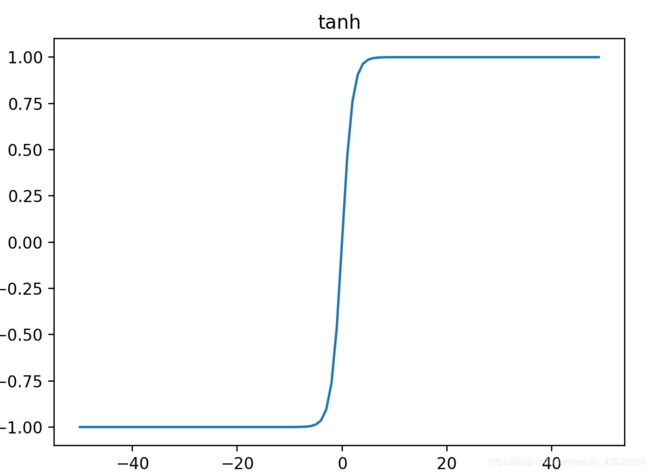
tanh是双曲函数中的一个,tanh()为双曲正切。在数学中,双曲正切“tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来,其函数表达式为:
g ( z ) = e z − e − z e z + e − z g(z) = {{e^z-e^{-z}}\over{e^z+e^{-z}}} g(z)=ez+e−zez−e−z
tanh其实是sigmoid经过放大后得到的:
t a n h ( z ) = 2 ∗ s i g m o i d ( z ) − 1 tanh(z) = 2*sigmoid(z)-1 tanh(z)=2∗sigmoid(z)−1
因此tanh的取值范围为 ( − 1 , 1 ) (-1,1) (−1,1),如下图
4.softmax函数
在数学,尤其是概率论和相关领域中,归一化指数函数,或称Softmax函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。该函数多于多分类问题中。
函数表达式为:
p ( y = i ) = e i ∑ j = 1 n e j p(y=i) = {{e^i}\over\sum_{j=1}^ne^j} p(y=i)=∑j=1nejei
二.卷积神经网络
2.1卷积神经网络的基本结构
卷积神经网络通常是又卷积层,池化层,全连接层组合而成,图8展示的是卷积神经网络中最经典的模型之一:VGG模型的网络结构。

其中conv代表卷积层,maxpool表示池化层,FC表示全连接层。
接下来我们来简述一下卷积神经网络中的卷积和池化是什么。
1.卷积
卷积概念的提出,是在信号与系统这么学科上,它的定义是一个信号(可以理解成一个函数)经过一个线性系统以后发生的变化。
对于连续信号(函数),卷积的定义为:
F ( t ) = ∫ x ( t − a ) w ( a ) d a F(t) = \int{x(t-a)}{w(a)}da F(t)=∫x(t−a)w(a)da
对于离散信号(函数),卷积的定义为:
F ( t ) = ∑ a x ( t − a ) w ( a ) F(t) = \sum_a{x(t-a)w(a)} F(t)=a∑x(t−a)w(a)
对于二维离散信号(函数)的卷积,定义为:
s ( i , j ) = ∑ m ∑ n x ( i − m , j − n ) w ( m , n ) s(i,j) = \sum_m\sum_n{x(i-m,j-n)w(m,n)} s(i,j)=m∑n∑x(i−m,j−n)w(m,n)
在卷积神经网络中,卷积的定义和上述定义略有不同,例如对于二维卷积,有:
s ( i , j ) = ∑ m ∑ n x ( i + m , j + n ) w ( w , n ) s(i,j) = \sum_m\sum_n{x(i+m,j+n)w(w,n)} s(i,j)=m∑n∑x(i+m,j+n)w(w,n)
虽然两个式子上形式上很相识,可是按照按个的数学定义来说是不同,产生两个式子不同的原因是因为对于普通二维信号的卷积,卷积核需要进行翻转操作,而在卷积神经网络的卷积中,卷积核不需要进行翻转操作。
卷积的作用:特征提取。
2.池化
池化是使用某一个位置的总体统计特征来代替网络在该位置的输出。例如最大池化(maxpooling)会给出相邻矩阵区域内的最大值。其他常用的池化函数包括平均值。 L 2 L^2 L2范数等。
池化的作用:
(1)帮助输入的表示近似不变。
(2)保留主要特征的同时减少参数个数(降维)。
2.2卷积神经网络的前向传播
1.卷积层
a l = σ ( z l ) = σ ( w l ∗ a l − 1 + b l ) a^l=\sigma(z^l) = \sigma(w^l*a^{l-1}+b^l) al=σ(zl)=σ(wl∗al−1+bl)
其中 σ ( z ) \sigma(z) σ(z)表示激活函数,一般为 R e l u Relu Relu函数。 ∗ * ∗表示卷积操作。
2.池化层
如果输入矩阵的大小为 m × m m×m m×m,池化层的filter大小为 k × k k×k k×k,则输出矩阵的大小为 m k × m k {m\over k}×{m\over k} km×km。
如果是最大值池化,则选取对应区域的最大值。如果是均值池化,则求对应区域的平均值。
3.全连接层
全连接层的前向传播和我们在第一部分讲述的一样,这里就不再重复,只给出对应的数学公式。
a l = σ ( z l ) = σ ( w l a l − 1 + b l ) a^l = \sigma(z^l) = \sigma(w^la^{l-1}+b^l) al=σ(zl)=σ(wlal−1+bl)
2.3卷积神经网络的反向传播
在进行CNN反向传播推到之前,回顾我们需要在第一部分反向传播中定义的 δ l δ^l δl,我们将根据 δ l δ^l δl来进行推到。
δ l = ∂ J ( w , x , b , y ) ∂ a l ∂ a l ∂ z l = ( a l − y ) ⋅ σ ′ ( z l ) δ^l = {∂J(w,x,b,y)\over∂a^l}{∂a^l\over∂z^l}=(a^l-y)·σ'(z^l) δl=∂al∂J(w,x,b,y)∂zl∂al=(al−y)⋅σ′(zl)
1.已知池化层的 δ l δ^l δl,推到上一层的 δ l − 1 δ^{l-1} δl−1
假设池化层的filter大小为2×2。
池化后的矩阵为:
[ 1 2 3 4 ] \begin{bmatrix} 1 &2\\ 3 & 4 \end{bmatrix} [1324]
如果我们用的最大值池化,我们对矩阵进行还原,即:
[ 0 0 0 0 0 1 2 0 0 3 4 0 0 0 0 0 ] \begin{bmatrix} 0&0&0&0\\0&1 &2&0\\ 0&3 & 4&0\\0&0&0&0 \end{bmatrix} ⎣⎢⎢⎡0000013002400000⎦⎥⎥⎤
如果我们用的均值池化,我们对矩阵进行还原,即:
[ 1 1 2 2 1 1 2 2 3 3 4 4 3 3 4 4 ] \begin{bmatrix} 1&1&2&2\\1&1 &2&2\\ 3&3 & 4&4\\3&3&4&4 \end{bmatrix} ⎣⎢⎢⎡1133113322442244⎦⎥⎥⎤
这样我们求出上一层的 δ l − 1 δ^{l-1} δl−1
δ l − 1 = ( ∂ a l − 1 ∂ z l − 1 ) T ∂ J ( w , b ) ∂ a l − 1 = u p s a m p l e ( δ l ) ⋅ σ ′ ( z l − 1 ) δ^{l-1}=({∂{a^{l-1}}\over{∂z^{l-1}}})^T{∂J(w,b)\over∂a^{l-1}}=upsample(δ^l)·\sigma'(z^{l-1}) δl−1=(∂zl−1∂al−1)T∂al−1∂J(w,b)=upsample(δl)⋅σ′(zl−1)
其中,upsample函数完成了池化误差矩阵放大与误差重新分配的逻辑。
2已知卷积层的 δ l δ^{l} δl,求上一层的 δ l − 1 δ^{l-1} δl−1
我们呢以及卷积层的前向传播公式为:
a l = σ ( z l ) = σ ( w l ∗ a l − 1 + b l ) a^l=\sigma(z^l) = \sigma(w^l*a^{l-1}+b^l) al=σ(zl)=σ(wl∗al−1+bl)
在DNN中,我们知道 δ l − 1 δ^{l−1} δl−1和 δ l δl δl存在递推关系,并且根据 z l z^l zl和 z l − 1 z^{l-1} zl−1的关系: z l = σ ( z l − 1 ) ∗ w l + b l z^l=\sigma(z^{l-1})*w^l+b^l zl=σ(zl−1)∗wl+bl,
因此我们有:
δ l − 1 = ( ∂ z l ∂ z l − 1 ) T δ l = δ l ∗ r o t 180 ( w l ) ⋅ σ ′ ( z l − 1 ) δ^{l-1}=({∂{z^l}\over{∂z^{l-1}}})^Tδ^{l}=δ^{l}*rot180(w^l)·\sigma'(z^{l-1}) δl−1=(∂zl−1∂zl)Tδl=δl∗rot180(wl)⋅σ′(zl−1)
含有卷积的式子求导时,卷积核被旋转了180度。即式子中的rot180(),翻转180度的意思是上下翻转一次,接着左右翻转一次。
假设 a l − 1 为 3 × 3 a^{l-1}为3×3 al−1为3×3矩阵,卷积核为2×2,pad=1.忽略 b l b^l bl,根据:
a l − 1 ∗ w l = z l a^{l-1}*w^l = z^l al−1∗wl=zl
具体为:
[ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] [ w 11 w 12 w 21 w 22 ] = [ z 11 z 12 z 21 z 22 ] \begin{bmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22} &a_{23}\\ a_{31} & a_{32}&a_{33} \end{bmatrix} \begin{bmatrix} w_{11}&w_{12}\\w_{21}&w_{22} \end{bmatrix} =\begin{bmatrix} z_{11}&z_{12}\\z_{21}&z_{22} \end{bmatrix} ⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤[w11w21w12w22]=[z11z21z12z22]
利用卷积的定义,我们知道:
z 11 = a 11 w 11 + a 12 w 12 + a 21 w 21 + a 22 w 22 z 12 = a 12 w 11 + a 13 w 12 + a 22 w 21 + a 23 w 22 z 21 = a 21 w 11 + a 22 w 12 + a 31 w 21 + a 32 w 22 z 22 = a 22 w 11 + a 23 w 12 + a 23 w 21 + a 33 w 22 \begin{array}{c}z_{11}=a_{11}w_{11}+a_{12}w_{12}+a_{21}w_{21}+a_{22}w_{22}\\z_{12}=a_{12}w_{11}+a_{13}w_{12}+a_{22}w_{21}+a_{23}w_{22}\\z_{21}=a_{21}w_{11}+a_{22}w_{12}+a_{31}w_{21}+a_{32}w_{22}\\z_{22}=a_{22}w_{11}+a_{23}w_{12}+a_{23}w_{21}+a_{33}w_{22} \end{array} z11=a11w11+a12w12+a21w21+a22w22z12=a12w11+a13w12+a22w21+a23w22z21=a21w11+a22w12+a31w21+a32w22z22=a22w11+a23w12+a23w21+a33w22
根据上式,我们对 a l − 1 a^{l-1} al−1求导:
∇ a 11 = δ 11 w 11 ∇ a 12 = δ 11 w 12 + δ 12 w 11 ∇ a 13 = δ 12 w 12 ∇ a 21 = δ 11 w 21 + δ 21 w 11 ∇ a 22 = δ 11 w 22 + δ 12 w 21 + δ 21 w 12 + δ 22 w 11 ∇ a 23 = δ 12 w 22 + δ 22 w 12 ∇ a 31 = δ 21 w 21 ∇ a 32 = δ 21 w 22 + δ 22 w 21 ∇ a 33 = δ 22 w 33 \begin{array}{c} ∇a_{11}=δ_{11}w_{11} \\∇a_{12}=δ_{11}w_{12}+δ_{12}w_{11} \\∇a_{13}=δ_{12}w_{12} \\∇a_{21}=δ_{11}w_{21}+δ_{21}w_{11} \\∇a_{22}=δ_{11}w_{22}+δ_{12}w_{21}+δ_{21}w_{12}+δ_{22}w_{11} \\∇a_{23}=δ_{12}w_{22}+δ_{22}w_{12} \\∇a_{31}=δ_{21}w_{21} \\∇a_{32}=δ_{21}w_{22}+δ_{22}w_{21} \\∇a_{33}=δ_{22}w_{33} \end{array} ∇a11=δ11w11∇a12=δ11w12+δ12w11∇a13=δ12w12∇a21=δ11w21+δ21w11∇a22=δ11w22+δ12w21+δ21w12+δ22w11∇a23=δ12w22+δ22w12∇a31=δ21w21∇a32=δ21w22+δ22w21∇a33=δ22w33
因此:
a l − 1 = [ ∇ a 11 ∇ a 12 ∇ a 13 ∇ a 21 ∇ a 22 ∇ a 23 ∇ a 31 ∇ a 32 ∇ a 33 ] a^{l-1}=\begin{bmatrix} ∇a_{11}&∇a_{12}&∇a_{13} \\∇a_{21}&∇a_{22}&∇a_{23} \\∇a_{31}&∇a_{32}&∇a_{33} \end{bmatrix} al−1=⎣⎡∇a11∇a21∇a31∇a12∇a22∇a32∇a13∇a23∇a33⎦⎤
以上就是卷积层的反向传播,接下来我们来求解 w , b w,b w,b的梯度
∂ J ( w , b ) ∂ w l = a l − 1 ∗ δ l {∂J(w,b)\over∂w^l}=a^{l-1}*δ^l ∂wl∂J(w,b)=al−1∗δl
对于 w i j w_{ij} wij我们有:
∂ J ( w , b ) ∂ w i j l = ∑ p ∑ q a i + p − 1 , j + q − 1 l − 1 δ p q l {∂J(w,b)\over∂w^l_{ij}}=\sum_p\sum_q{a^{l-1}_{i+p-1,j+q-1}δ^l_{pq}} ∂wijl∂J(w,b)=p∑q∑ai+p−1,j+q−1l−1δpql
对于 b l b^l bl,我们有:
∂ J ( w , b ) ∂ b l = ∑ w , v δ w , v l {∂J(w,b)\over∂b^l}=\sum_{w,v}δ^l_{w,v} ∂bl∂J(w,b)=w,v∑δw,vl
上述内容就是CNN反向传播的全部过程。
三.用numpy搭建神经网络
本部分在仅导入numpy包的条件下实现对神经网络的搭建。
3.1DNN的numpy实现:
1.定义激活函数以及激活函数的导数:
def sigmod(x):
return 1/(1+np.exp(-x))
def relu(x):
if x >= 0:
return x
else:
return 0
def relu_backward(dA, cache):
"""
cache - 缓存了一些反向传播函数conv_backward()需要的一些数据
"""
Z = cache
dz = np.array(dA,copy = True)
dz[Z<=0] = 0
return dz
def sigmoid_backward(dA, cache):
"""
cache - 缓存了一些反向传播函数conv_backward()需要的一些数据
"""
z = cache
s = 1/(1+np.exp(-z))
dz = dA*s*(1-s)
return dz
2参数w,b初始化:
def init_parameter(layers_dim):
"""
layers_dim:DNN中各层的节点数
"""
np.random.seed(3)
parameters = {}
for i in range(1,len(layers_dim)):
#parameters['w'+str(i)] = np.random.randn(layers_dim[i],layers_dim[i-1])*0.01
parameters['w' + str(i)] = np.random.randn(layers_dim[i], layers_dim[i - 1]) *np.sqrt(2/layers_dim[i-1])
parameters['b'+str(i)] = np.zeros((layers_dim[i],1))
#print(str(i)+"+"+str(parameters["w"+str(i)].shape)+"+"+str(parameters['b'+str(i)].shape))
return parameters
3.定义前向传播函数:
def linear_forward(A,w,b):
"""
实现前向传播的线性部分。
参数:
A - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量)
W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量)
b - 偏向量,numpy向量,维度为(当前图层节点数量,1)
返回:
Z - 激活功能的输入,也称为预激活参数
cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递
"""
z = np.dot(w,A)+b
cache = (A,w,b)
return z,cache
def linear_activation_forward(A_prev,w,b,activation):
"""
A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数)
activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递
"""
if activation == 'sigmoid':
Z, linear_cache = linear_forward(A_prev, w, b)
A,activation_cache = sigmoid(Z)
elif activation =='relu':
Z, linear_cache = linear_forward(A_prev, w, b)
A ,activation_cache= relu(Z)
cache = (linear_cache,activation_cache)
return A,cache
def L_model_forward(X,parameters):
"""
AL - 最后的激活值
caches - 包含以下内容的缓存列表:
linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2)
linear_sigmoid_forward()的cache(只有一个,索引为L-1)
"""
caches = []
A = X
L = len(parameters) // 2
for l in range(1,L):
A_prev = A
A,cache = linear_activation_forward(A_prev,parameters['w'+str(l)],parameters['b'+str(l)],'relu')
caches.append(cache)
A_prev = A
AL,cache = linear_activation_forward(A_prev,parameters['w'+str(L)],parameters['b'+str(L)],'sigmoid')
caches.append(cache)
return AL,caches
4.计算损失:
def compute_cost(Y,AL):
"""
AL - 与标签预测相对应的概率向量,维度为(1,示例数量)
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
"""
m = Y.shape[1]
cost = -1/m*np.sum(np.multiply(np.log(AL),Y)+np.multiply(np.log(1-AL),(1-Y)))
cost = np.squeeze(cost)
return cost
5.定义反向传播函数:
def linear_backward(dz,cache):
"""
为单层实现反向传播的线性部分(第L层)
参数:
dZ - 相对于(当前第l层的)线性输出的成本梯度
cache - 来自当前层前向传播的值的元组(A_prev,W,b)
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度,与W的维度相同
db - 相对于b(当前层l)的成本梯度,与b维度相同
"""
A_prev,w,b = cache
m = A_prev.shape[1]
dw = np.dot(dz,A_prev.T)/m
db = np.sum(dz,axis=1,keepdims=True)/m
dA_prev = np.dot(w.T,dz)
return dA_prev,dw,db
def linear_activation_backward(dA,cache,activation):
"""
实现LINEAR-> ACTIVATION层的后向传播。
参数:
dA - 当前层l的激活后的梯度值
cache - 我们存储的用于有效计算反向传播的值的元组(值为linear_cache,activation_cache)
activation - 要在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度值,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度值,与W的维度相同
db - 相对于b(当前层l)的成本梯度值,与b的维度相同
"""
linear_cache,activation_cache = cache
if activation == "relu":
dz = relu_backward(dA,activation_cache)
dA_prev,dw,db = linear_backward(dz,linear_cache)
elif activation == "sigmoid":
dz = sigmoid_backward(dA,activation_cache)
dA_prev,dw,db = linear_backward(dz,linear_cache)
return dA_prev,dw,db
def L_model_backward(AL,Y,caches):
"""
grads - 具有梯度值的字典
grads [“dA”+ str(l)] = ...
grads [“dW”+ str(l)] = ...
grads [“db”+ str(l)] = ...
"""
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = -(np.divide(Y,AL)-np.divide(1-Y,1-AL))
current_cache = caches[L-1]
grads["dA"+str(L)],grads["dw"+str(L)],grads["db"+str(L)] = linear_activation_backward(dAL,current_cache,"sigmoid")
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp,dw_temp,db_temp = linear_activation_backward(grads["dA"+str(l+2)],current_cache,"relu")
grads["dA"+str(l+1)] = dA_prev_temp
grads["dw"+str(l+1)] = dw_temp
grads["db"+str(l+1)] = db_temp
return grads
6.参数更新:
使用梯度下降法,对参数进行更新
def update_parameters(parameters,grads,learning_rate = 0.1):
L = len(parameters)//2
for l in range(L):
parameters["w"+str(l+1)] -= learning_rate*grads["dw"+str(l+1)]
parameters["b"+str(l+1)] -= learning_rate*grads["db"+str(l+1)]
return parameters
7.模型定义:
def dnn_model(X_total,Y_total,layers_dims,num_iterations = 10000,print_cost = True):
np.random.seed(1)
costs = []
batchsize = 16
parameters = init_parameter(layers_dims)
v,s = init_adam(parameters)
t = 0
for i in range(0,num_iterations):
X,Y = batch_data(X_total,Y_total,batchsize)
AL,caches = L_model_forward(X,parameters)
cost = compute_cost(Y,AL)
# acc = comput_arccuracy(Y,AL)
grads = L_model_backward(AL,Y,caches)
t = t+1
parameters,v,s = update_parameters_with_Adam(parameters,grads,v,s,t)
if print_cost and i%100 == 0:
print("cost after iteration %i:%f"%(i,cost))
costs.append(cost)
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens')
plt.show()
test_file_path = "C:\\Users\\10372\\Desktop\\Learning\\机器学习\\数据集\\考生本地用资源\\test_data.txt"
test_x,test_y = data(test_file_path)
AL, caches = L_model_forward(test_x, parameters)
cost = compute_cost(test_y, AL)
print("test cost is %f"%(cost))
return parameters
完整代码请参看:
链接: CNN代码.
3.2 CNN的numpy实现:
1.卷积层的前向传播:
def zero_pad(X,pad):
x_paded = np.pad(X,(
(0,0),
(pad,pad),
(pad,pad),
(0,0)),
'constant',constant_values=0)
return x_paded
def conv_single_step(a_slice_prev,w,b):
s = np.multiply(a_slice_prev,w)+b
z = np.sum(s)
return z
def conv_forward(A_prev, W, b, hparameters):
# 获取来自上一层数据的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 获取权重矩阵的基本信息
(f, f, n_C_prev, n_C) = W.shape
# 获取超参数hparameters的值
stride = hparameters["stride"]
pad = hparameters["pad"]
n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
n_W = int((n_W_prev - f + 2 * pad) / stride) + 1
Z = np.zeros((m, n_H, n_W, n_C))
A_prev_pad = zero_pad(A_prev, pad)
for i in range(m):
a_prev_pad = A_prev_pad[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + f
a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[0, 0, 0, c])
assert (Z.shape == (m, n_H, n_W, n_C))
cache = (A_prev, W, b, hparameters)
return (Z, cache)
2.池化层的前向传播:
def pool_forward(A_prev,hparameters,mode = "max"):
(m, n_H_prev, n_W_prev, n_c_prev) = A_prev.shape
f = hparameters["f"]
stride = hparameters["stride"]
n_H = int((n_H_prev - f) / stride) + 1
n_W = int((n_W_prev - f) / stride) + 1
n_C = n_c_prev
A = np.zeros((m,n_H,n_W,n_C))
for i in range(m): # 遍历样本
for h in range(n_H): # 在输出的垂直轴上循环
for w in range(n_W): # 在输出的水平轴上循环
for c in range(n_C): # 循环遍历输出的通道
# 定位当前的切片位置
vert_start = h * stride # 竖向,开始的位置
vert_end = vert_start + f # 竖向,结束的位置
horiz_start = w * stride # 横向,开始的位置
horiz_end = horiz_start + f # 横向,结束的位置
# 定位完毕,开始切割
a_slice_prev = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]
# 对切片进行池化操作
if mode == "max":
A[i, h, w, c] = np.max(a_slice_prev)
elif mode == "average":
A[i, h, w, c] = np.mean(a_slice_prev)
cache = (A_prev,hparameters)
return (A,cache)
3.卷积层的反向传播:
def conv_backward(dZ, cache):
# 获取cache的值
(A_prev, W, b, hparameters) = cache
# 获取A_prev的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 获取dZ的基本信息
(m, n_H, n_W, n_C) = dZ.shape
# 获取权值的基本信息
(f, f, n_C_prev, n_C) = W.shape
# 获取hparaeters的值
pad = hparameters["pad"]
stride = hparameters["stride"]
# 初始化各个梯度的结构
dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
dW = np.zeros((f, f, n_C_prev, n_C))
db = np.zeros((1, 1, 1, n_C))
# 前向传播中我们使用了pad,反向传播也需要使用,这是为了保证数据结构一致
A_prev_pad = zero_pad(A_prev, pad)
dA_prev_pad = zero_pad(dA_prev, pad)
# 现在处理数据
for i in range(m):
# 选择第i个扩充了的数据的样本,降了一维。
a_prev_pad = A_prev_pad[i]
da_prev_pad = dA_prev_pad[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
# 定位切片位置
vert_start = h
vert_end = vert_start + f
horiz_start = w
horiz_end = horiz_start + f
# 定位完毕,开始切片
a_slice = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
# 切片完毕,使用上面的公式计算梯度
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:, :, :, c] * dZ[i, h, w, c]
dW[:, :, :, c] += a_slice * dZ[i, h, w, c]
db[:, :, :, c] += dZ[i, h, w, c]
# 设置第i个样本最终的dA_prev,即把非填充的数据取出来。
dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :]
# 数据处理完毕,验证数据格式是否正确
assert (dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return (dA_prev, dW, db)
4.池化层的反向传播:
def create_mask_from_window(x):
mask = x == np.max(x)
return mask
def distribute_value(dz, shape):
# 获取矩阵的大小
(n_H, n_W) = shape
# 计算平均值
average = dz / (n_H * n_W)
# 填充入矩阵
a = np.ones(shape) * average
return a
def pool_backward(dA, cache, mode="max"):
# 获取cache中的值
(A_prev, hparaeters) = cache
# 获取hparaeters的值
f = hparaeters["f"]
stride = hparaeters["stride"]
# 获取A_prev和dA的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(m, n_H, n_W, n_C) = dA.shape
# 初始化输出的结构
dA_prev = np.zeros_like(A_prev)
# 开始处理数据
for i in range(m):
a_prev = A_prev[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
# 定位切片位置
vert_start = h
vert_end = vert_start + f
horiz_start = w
horiz_end = horiz_start + f
# 选择反向传播的计算方式
if mode == "max":
# 开始切片
a_prev_slice = a_prev[vert_start:vert_end, horiz_start:horiz_end, c]
# 创建掩码
mask = create_mask_from_window(a_prev_slice)
# 计算dA_prev
dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += np.multiply(mask, dA[i, h, w, c])
elif mode == "average":
# 获取dA的值
da = dA[i, h, w, c]
# 定义过滤器大小
shape = (f, f)
# 平均分配
dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += distribute_value(da, shape)
# 数据处理完毕,开始验证格式
assert (dA_prev.shape == A_prev.shape)
return dA_prev
四.参考资料
1.【吴恩达课后编程作业】01 - 神经网络和深度学习 - 第四周 - PA1&2 - 一步步搭建多层神经网络以及应用
2.【中文】【吴恩达课后编程作业】Course 4 - 卷积神经网络 - 第一周作业 - 搭建卷积神经网络模型以及应用(1&2)
3.刘建平Pinard的博客

