numpy 的transpose是如何实现的

背景

transpose在深度学习中是很常见的一个操作, numpy和pytorch都有对应的操作, 但是内部是如何实现的呢? stackoverflow上有很相信的说明, 这里搬运下.

transpose 是如何工作的?

• 定义一个数组看看transpose的结果如何

In [28]: arr = np.arange(16).reshape((2, 2, 4))

In [29]: arr
Out[29]: 
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])


In [32]: arr.transpose((1, 0, 2))
Out[32]: 
array([[[ 0,  1,  2,  3],
        [ 8,  9, 10, 11]],

       [[ 4,  5,  6,  7],
        [12, 13, 14, 15]]])

在np.array中, 对于三维数组的三个轴的定义如下:

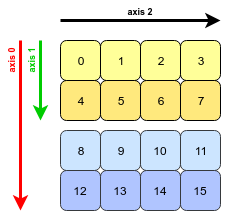
数组内部实现上其实是使用一块连续内存保存数据的,在内存空间里, 这些数据的保存形式:

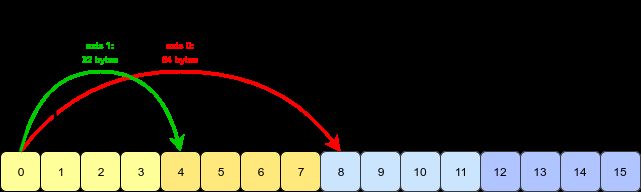
上图中的64 bytes, 32 bytes, 8bytes,为0, 1, 2三个轴的stride,换句话说, 在三个轴上取数时要用不同的stride跳跃, 轴0上每增加一位则要跳64bytes, 假如取(i, j, k)位的数arr[i, j, k], 那么可以知道:

# 这里的strides表示的位数,不是byte, 对于上图strides则为[8, 4, 1]
idx = strides[0] * i + strides[1] * j + strides[2] *k
arr[i, j, k] = buffer[idx]

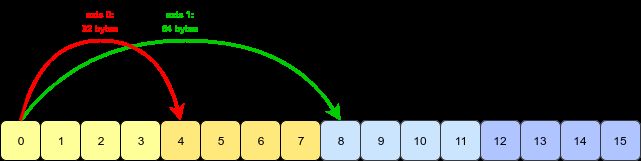
当做arr.transpose(1, 0, 2)操作时, 需要将每个轴的dim和stride都换下,

strides变化:[64, 32, 8] ----------> [32, 64, 8]
shapes 变化:[2, 2, 4] ----------------> [2, 2, 4]
这样就避免了内存拷贝, transpose几乎无时间消耗.

代码实现

下面定义一个tensor来实现 transpose, 注意transpose时仅仅对strides, shapes做了顺序交换. 这里的strides表示的element移动个数,而不是bytes.

class Tensor:
    def __init__(self, data_lst, shapes):
        assert len(shapes) == 3
        self.data = data_lst
        self.shapes = np.array(list(shapes))
        self.strides = np.array([shapes[1] * shapes[2], shapes[2], 1])

    def print(self) -> str:
        print('(')
        for i in range(self.shapes[0]):
            print('[', end = '')
            for j in range(self.shapes[1]):
                print('[', end = '')
                for k in range(self.shapes[2]):
                    idx = i * self.strides[0] + j * self.strides[1] + k * self.strides[2]
                    print(self.data[idx], ' ', end = '')
                print(']', end = '') 
            print(']')
        print(')')
    
    def transpose(self, axes):
        assert len(axes) == len(self.shapes)
        axes = list(axes)
        self.shapes = self.shapes[axes]
        self.strides = self.strides[axes]
        return self

    def numpy(self):
        """ convert to numpy array

        Returns:
            _type_: np.ndarray
        """
        n_elements = self.shapes[0] * self.shapes[1] * self.shapes[2]
        arr = np.zeros((n_elements,))
        target_idx = 0
        for i in range(self.shapes[0]):
            for j in range(self.shapes[1]):
                for k in range(self.shapes[2]):
                    src_idx = i * self.strides[0] + j * self.strides[1] + k * self.strides[2]
                    arr[target_idx] = self.data[src_idx]
                    target_idx += 1
        return arr.reshape(self.shapes)

def test_tensor():
    axes = [1, 0, 2]
    arr = np.arange(16).reshape((2, 2, 4))
    t = Tensor(arr.reshape(-1).tolist(), (2, 2, 4))
    print('original arr:')
    t.print()
    print('numpy.transpose:', np.transpose(arr, axes))
    ret = t.transpose(axes).numpy()
    print('after transpose:', ret)
    assert np.allclose(np.transpose(arr, axes), ret)