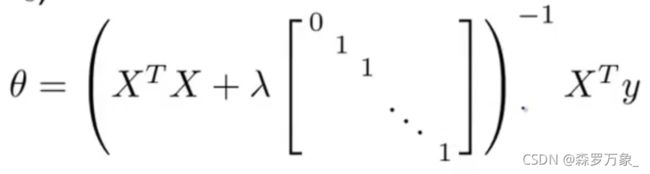_森罗万象

临床大数据分析与挖掘

文章目录

一、数据准备
- 1.数据质量校验
- - 1.1.一致性校验
  - - 1.1.1.时间校验
    - 1.1.2.字段信息校验
  - 1.2.缺失值校验
  - 1.3.异常值校验
- 2.数据分布与趋势探查
- - 2.1.分布分析
  - - 2.1.1.定量数据分析
    - 2.2.2.定性数据分析
  - 2.2.对比分析
  - - 2.2.1.对比分析的形式
    - 2.2.2.对比分析的标准
  - 2.3.描述性统计分析
  - 2.4.周期性分析
  - 2.5.贡献度分析
  - 2.6.相关性分析
- 3.数据清洗
- - 3.1.缺失值处理
  - - 3.1.1.删除
    - 3.1.2.数据插补
    - 3.1.3.不处理
  - 3.2.异常值处理
- 4.数据合并
- - 4.1.数据堆叠
  - 4.2.主键合并
二、特征工程
- 1.特征变换
- - 1.1.标准化
  - 1.2.独热编码
  - 1.3.离散化
  - - 1.3.1.等宽法
    - 1.3.2.等频法
    - 1.3.3.基于聚类分析的方法
- 2.特征选择
- - 2.1.子集搜索与评价
  - 2.2.过滤式选择
  - 2.3.包裹式选择
  - 2.4.嵌入式选择与L1范数正则化
  - 2.5.稀疏表示与字典学习
三、有监督学习
- 1.有监督学习简介
- 2.度量性能
- - 2.1.分类任务性能度量
  - - 2.1.1.正确率和错误率
    - 2.1.2.精确率、召回率和F1度量
    - 2.1.3.ROC曲线
  - 2.2.回归任务性能度量
- 3.线性模型
- - 3.1.线性模型简介
  - 3.2.线性回归
  - 3.3.逻辑回归
- 4.k近邻分类
- 5.决策树
- 6.支持向量机
- - 6.1支持向量机简介
  - 6.2.线性支持向量机
  - 6.3.非线性支持向量机
- 7.朴素贝叶斯
- 8.神经网络
- - 8.1.神经网络介绍
  - 8.2.BP神经网络
- 9.集成学习
- - 9.1.Bagging
  - 9.2.Boosting
  - 9.3.Stacking
四、无监督学习
- - 1.无监督学习简介
  - 2.降维
  - - 2.1.PCA
    - 2.2.核化线性降维
  - 3.聚类任务
  - - 3.1.聚类性能度量指标
    - 3.2.距离计算
    - 3.3.原型聚类
    - - 3.3.1.K-Means算法
      - 3.3.2.学习向量量化算法
      - 3.3.3.高斯混合聚类
    - 3.4.密度聚类
    - 3.5.层次聚类
  - 4.异常检测
五、投入应用
六、应用案例
- 1.医疗保险的欺诈发现
- - 1.1.目标分析
  - - 1.1.1.数据说明
    - 1.1.2.分析目标
  - 1.2.数据准备
  - - 1.2.1.描述性统计分析
    - 1.2.2.数据清洗
  - 1.3.特征工程
  - - 1.3.1.特征选择
    - 1.3.2.特征变换
    - - 1.3.2.1.投保人特征变换
      - 1.3.2.2.医疗机构特征变换
  - 1.4.模型训练
  - 1.5.性能度量
  - - 1.5.1.结果发现
    - 1.5.2.聚类性能度量
根据类群的迁移变化选择出疑似欺诈的情况

所用数据

吴恩达课程

练习所用数据

Python代码

一、数据准备

数据准备所消耗时间占整个机器学习项目总体时间的80%。

1.数据质量校验

1.1.一致性校验

数据不一致型是指各类数据的矛盾性和不相容性,经常由数据冗余,并发性控制不当或各种错误造成.具体包括:

1.1.1.时间校验

时间范围不一致:一张表的数据是从1-2.1,另一张表数据从15-2.15

时间粒度不一致:一张表的数据隔30秒取一次,另一张表隔1分钟取一次

时间格式不一致:2016-10-01和20161001

时区不一致:海外服务器没有修改时区,导致数据在传回本地由于时区差异造成时间不一致

1.1.2.字段信息校验

同名异义:字段名称相同,表达实际意义不同

异名同义:名称不同的字段代表的实际意义相同

单位不统一:两个名称相同的字段所代表的实际意义一致,如都表示金钱,但单位不同,如一个以元为单位,一个以美元为单位

1.2.缺失值校验

缺失值表示现有数据集中某个或某些特征的值是不完全的

>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\food_coded.csv')
>>> data
     Gender  cuisine  drink
0         2      NaN    0
1         1      0    2.0
2         1      3.0    0
3         1      2.0    2.0
4         1      2.0    2.0
5         1      NaN    2.0
...
124   False    False  False

[125 rows x 3 columns]
>>> data.count() #非空元素计数
Gender     125 
cuisine    108
drink      123
dtype: int64
>>> 1-data.count()/len(data) #缺失率
Gender     0.000
cuisine    0.136
drink      0.016
dtype: float64

1.3.异常值校验

假设数据符合正太分布,一组数据中与均值的偏差超过2倍标准差的数据称为异常值,这称为四分位距(IQR)准则;一组数据中与均值的偏差超过3倍标准差的数据称为高度异常值,这称为3σ原则

>>> array = (51,2618.2,2608.4,2659,3442.1,3393.1,3136.1,3744.1,6607.4,4060.3,3614.7,3295.5,2332.1,2699.3,3036.8, 865,3014.3,2742.8,2173.5)
>>> Percentile=np.percentile(array,[0,25,50,75,100]) #计算分位数
>>> Percentile
array([  5 , 2613.3, 3014.3, 3417.6, 6607.4])
>>> IQR=Percentile[3] - Percentile[1]
>>> UpLimit = Percentile[3]+IQR*5             #异常值上界Q3+5IQR
>>> arrayownLimit = Percentile[1]-IQR*5       #异常值下界Q1-5IQR
>>> abnormal = [i for i in array if i >UpLimit or i < arrayownLimit]
>>> abnormal 		#四分位距准则测得的异常值
[51, 6607.4, 865]
>>> array_mean=np.array(array).mean()
>>> array_sarray=np.array(array).std()     #计算标准差
>>> array_cha=array-array_mean
>>> index = [i for i in range(len(array_cha)) if np.abs(array_cha[i])>3*array_sarray]
>>> abnormal = [array[i] for i in index]
>>> abnormal        #3σ原则检测出的异常值
[]

2.数据分布与趋势探查

2.1.分布分析

2.1.1.定量数据分析

定量分析一般按照以下步骤进行:

求极差

决定组距和组数

决定分点

列出频率分布表

绘制频率分布直方图

>>>sale=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\lh.csv',encoding='gbk')
>>> sale=np.array(sale)
>>> sale_jicha=max(sale)-min(sale)
>>> sale_jicha
array([2.1])
>>> group=round(sale_jicha[0]/0.25)     #组数
>>> bins=np.linspace(min(sale),max(sale),group)   #分割点位置
>>> zuju=bins[1]-bins[0]     #组距
>>> bins
array([[4],
       [7],
       [2. ],
       [2.3],
       [2.6],
       [2.9],
       [3.2],
       [3.5]])
>>> zuju
array([0.3])

# 绘制频率分布表
table_fre = pd.DataFrame(np.zeros([6,5]),columns = ['组段','组中值x','频数','频率f','累计频率'])
f_sum = 0  # 累计频率初始值
for i in range(len(bins)):
        table_fre.iloc[i,'组段'] = '['+str(round(bins[i][0],2))+','+str(round((bins[i][0]+zuju)[0],2))+')'
        table_fre.iloc[i,'组中值x'] = round(np.array((bins[i],bins[i]+zuju)).mean (),2)
        table_fre.iloc[i,'频数'] = sum([pd.notnull(j) for j in sale if bins[i] <= j <bins[i]+zuju])
        table_fre.iloc[i,'频率f'] = table_fre.iloc[i,'频数']/len(sale)
        f_sum = f_sum + table_fre.iloc[i,'频率f']
        table_fre.iloc[i,'累计频率'] = f_sum 
print('频率分布表为：\n',table_fre)

# 计算频率与组距的比值，作为频率分布直方图的纵坐标
y = table_fre.iloc[:,'频率f']/zuju
# 绘制频率分布直方图
fig = plt.figure(figsize=(14,4))
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 
ax = fig.add_subplot(111)
plt.bar(table_fre.iloc[:,'组段'],y,0.8)
plt.xlabel('分布区间')
plt.ylabel('频率/组距')
plt.title('频率分布直方图')
plt.show()

2.2.2.定性数据分析

对定性数据进行分布分析一般用饼图和条形图

>>>data=pd.read_csv('C:\\Users\\PC\Desktop\\Two\\data\\ldeaths.csv',encoding='gbk')
>>> plt.pie(data.iloc[:,1],labels=data.iloc[:,0],autopct='%2f%%')
>>> plt.rcParams['font.sans-serif'] = ['SimHei']
>>> plt.rcParams['axes.unicode_minus'] = False
>>> plt.title('死亡人数分布饼图')
Text(0.5,1,'死亡人数分布饼图')
>>> plt.show()
>>> plt.bar(data.iloc[:,0],data.iloc[:,1])
<BarContainer object of 12 artists>
>>> plt.xlabel('月份')
Text(0.5,0,'月份')
>>> plt.ylabel('死亡人数')
Text(0,0.5,'死亡人数')
>>> plt.rcParams['font.sans-serif'] = ['SimHei']
>>> plt.rcParams['axes.unicode_minus'] = False
>>> plt.title('死亡人数分布条形图')
Text(0.5,1,'死亡人数分布条形图')
>>> plt.show()

2.2.对比分析

2.2.1.对比分析的形式

对比分析的形式有绝对数比较和相对数比较,相对数还可以分为

动态相对数:将同一现象在不同时期的指标数值进行比较用以说明发展方向和变化速度

强度相对数:将两个性质不同但有一定联系的总量指标进行对比,用以说明现象的强度,密度和普遍程度

比例相对数:将同一总体的不同部分数值进行对比

比较相对数:将同一时期两个性质相同的指标数值进行对比,说明同类现象在不同空间条件下的的数量对比关系

计划完成程度相对数:将某一时期实际完成数与计划数进行对比

结构相对数:将同一总体内的部分数值与全部数值对比求得比重

2.2.2.对比分析的标准

计划标准:将实际数据与计划数对比

经验标准或理论标准:将实际数据与资料归纳或理论推导的标准对比

时间标准:将实际数据与上一时期或历史最好水平或历史关键时期进行比较

空间标准:选择不同的空间指标数据进行比较,主要包括相似空间的比较,与先进空间的比较和空大空间比较三种

>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\Store sales.csv',encoding='gbk')
>>> data
           日期  店铺1  店铺2   店铺3   店铺4
0    2013/1/2  668  650   805  1429
1    2013/1/3  578  555   721  1248
2    2013/1/4  619  574   690  1232
3    2013/1/5  635  324   525  1514
4    2013/1/7  785  763  1079  1562
...
25  2013/1/31  571  517   648  1355
>>> plt.rcParams['font.sans-serif'] = ['SimHei']
>>> plt.rcParams['axes.unicode_minus'] = False
>>> plt.figure(figsize=(8,4))
<Figure size 800x400 with 0 Axes>
>>> linestyle=['-','--',':','-.']
>>> for i in range(4):
...     plt.plot(data['日期'],data.iloc[:,i+1],linestyle=linestyle[i])
>>> plt.xticks(data['日期'])
([<matplotlib.axis.XTick object at 0x000001E840C04AC8>, <matplotlib.axis.XTick object at 0x000001E840C04400>, <matplotlib.axis.XTick object at 0x000001E840C042E8>, <matplotlib.axis.XTick object at 0x000001E840C37C88>, <matplotlib.axis.XTick object at 0x000001E840C40198>, <matplotlib.axis.XTick object at ...
0x000001E840C608D0>], <a list of 26 Text xticklabel objects>)
>>> ax=plt.gca()
>>> from matplotlib.pyplot import MutipleLocator
>>> ax.xaxis.set_major_locator(plt.MultipleLocator(4))
>>> plt.title('四个店铺的订单量折线图')
Text(0.5,1,'四个店铺的订单量折线图')
>>> plt.legend()
<matplotlib.legend.Legend object at 0x000001E840C0DE80>
>>> plt.show()

2.3.描述性统计分析

集中程度度量指标有:均值,中位数,众数

离散程度度量指标有:

极差

四分位差:指上四分位数和下四分位数之差,四分位差反映了中间50%数据的离散程度,其数值越小说明离散程度越小,即数据的变异程度越小

标准差,方差

变异系数:变异系数用来度量标准差相对于均值的离中趋势,它是刻画数据相对分散性的一种度量,记为CV,计算公式为

CV=(标准差/均值)*100%

变异系数主要用来比较两个或多个具有不同单位或不同波动幅度的数据集的离中程度

>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\Drug sales.csv',encoding='gbk')
>>> data
         Date  Sales
0    2015/7/1   5223
1    2015/7/2   5558
2    2015/7/3   4665
3    2015/7/4   4797
4    2015/7/6   4359
5    2015/7/7   3650
...
26  2015/7/31   5263
>>> explore=data.describe().T
>>> explore
       count         mean         std   ...       50%     75%     max
Sales   27.0  449333333  693.377908   ...    4427.0  5015.5  6102.0

[1 rows x 8 columns]
>>> explore['jicha']=explore['max']-explore['min']
>>> explore['IQR']=explore['75%']-explore['25%']
>>> explore['CV']=explore['std']/explore['mean']
>>> explore['std_2']=explore['std']**2
>>> explore['median']=np.median(data.iloc[:,1])
>>> explore['zhongshu']=np.argmax(np.bincount(data.iloc[:,1]))
>>> explore.T
                  Sales
count         27.000000
mean        449333333
std          693.377908
min         3464.000000
25%         3802.500000
50%         4427.000000
75%         5015.500000
max         6102.000000
jicha       2638.000000
IQR         1213.000000
CV             0.154381
std_2     480772.923077
median      4427.000000
zhongshu    3464.000000

2.4.周期性分析

按照时间尺度进行划分,周期性趋势按时间粒度的常用划分是年度周期性趋势,季周期性趋势,月度周期性趋势,周度周期性趋势和天,小时周期性趋势.对数据进行周期性分析,能达到掌握数据周期性变动规律的目的

2.5.贡献度分析

贡献度分析又称为帕累托分析,它的原理是帕累托法则(28定律),即同样的投入放在不同的地方会产生不同的效益.对于一个公司来说,80%的利润常常来自于20%最畅销的产品,而其他80%的产品只产生了20%的利润

贡献度分析需要绘制帕累托图,又称为排列图,主次图,是按照发生频率大小的顺序绘制直方图,表示有多说结果是由以已确认类型或范畴的原因造成的.贡献度分析可以用来分析质量问题,确定产生质量问题的主要因素.帕累托图用双直角坐标系表中,左边纵坐标表示频数,右边纵坐标表示频率.横坐标表示影响质量的各项因素,按照影响程度的大小(即出现的频数的多少)从左到右排列.改图可以判断影响质量的主要因素

>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\contribution.csv',encoding='gbk')
>>> plt.rcParams['font.sans-serif'] = ['SimHei']
>>> plt.rcParams['axes.unicode_minus'] = False
>>> data
    店铺名     月利润
0   店铺1  121266
1   店铺2  133765
2   店铺3  183535
3   店铺4  276935
4   店铺5  124190
5   店铺6  120637
6   店铺7  277959
7   店铺8  175011
8   店铺9  194575
9  店铺10  162713
>>> data=data.set_index('店铺名')
>>> data
         月利润
店铺名         
店铺1   121266
店铺2   133765
店铺3   183535
店铺4   276935
店铺5   124190
店铺6   120637
店铺7   277959
店铺8   175011
店铺9   194575
店铺10  162713
>>> data=data.sort_values('月利润',ascending=False)
>>> data
         月利润
店铺名         
店铺7   277959
店铺4   276935
店铺9   194575
店铺3   183535
店铺8   175011
店铺10  162713
店铺2   133765
店铺5   124190
店铺1   121266
店铺6   120637
>>> data.plot(kind='bar')
<matplotlib.axes._subplots.AxesSubplot object at 0x000001B9FE20EE80>
#折线图
>>> data=data['月利润'].cumsum()/data['月利润'].sum()
>>> data
店铺名
店铺7     0.156987
店铺4     0.313396
店铺9     0.423289
店铺3     0.526946
店铺8     0.625790
店铺10    0.717688
店铺2     0.793236
店铺5     0.863377
店铺1     0.931866
店铺6     000000
Name: 月利润, dtype: float64
>>> data.plot(color='black',secondary_y=True,style='-x',linewidth=2)
<matplotlib.axes._subplots.AxesSubplot object at 0x000001B9FFB647F0>
#添加标注
>>> data=data.reset_index(drop=True)
>>> data
0    0.156987
1    0.313396
2    0.423289
3    0.526946
4    0.625790
5    0.717688
6    0.793236
7    0.863377
8    0.931866
9    000000
Name: 月利润, dtype: float64
>>> data=data[data>=0.8][0:1]
>>> data
7    0.863377
Name: 月利润, dtype: float64
>>> point_x=data.index[0]
>>> point_x
7
>>> point_y=data[point_x]
>>> point_y
0.8633768707083418
>>> plt.annotate(format(point_y, '.2%'), xy = (point_x, point_y),xytext=(point_x*0.9, point_y*0.9), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
Text(6.3,0.777039,'86.34%')
>>> plt.ylabel('利润(元)')
Text(0,0.5,'利润(元)')
>>> plt.ylabel('利润(比例)')
Text(0,0.5,'利润(比例)')
>>> plt.show()

2.6.相关性分析

判断两个变量是否具有关系的最直观方法是绘制散点图,但有时要考虑多个变量之间的关系,如果利用散点图进行相关性分析,那么需要对变量两两绘制散点图,使工作变得复杂.相关性热力图是解决这个问题的好方法,它可以快速发现多个变量之间的相关性

相关系数是一种统计指标,一般用r表示.由于研究对象的不同,相关系数有多种定义方式,主要有Person相关系数,Spearman相关系数,Kendall等级相关系数,判定系数

>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\Dataset_spine.csv',encoding='gbk')
>>> data
          Col1       Col2       Col3       Col4        Col5
0    63.027818  22.552586  39.609117  40.475232   98.672917
1    39.056951  10.060991  25.015378  28.995960  114.405425
2    68.832021  22.218482  50.092194  46.613539  105.985135
3    69.297008  24.652878  44.311238  44.644130  10868495
4    49.712859   9.652075  28.317406  40.060784  108.168725
5    40.250200  13.921907  25.124950  26.328293  130.327871
...
309  33.841641   5.073991  36.641233  28.767649  123.945244

[310 rows x 5 columns]
>>> data.corr()   #任意两列的相关系数矩阵
          Col1      Col2      Col3      Col4      Col5
Col1  000000  0.629199  0.717282  0.814960 -0.247467
Col2  0.629199  000000  0.432764  0.062345  0.032668
Col3  0.717282  0.432764  000000  0.598387 -0.080344
Col4  0.814960  0.062345  0.598387  000000 -0.342128
Col5 -0.247467  0.032668 -0.080344 -0.342128  000000
>>> data['Col1'].corr(data['Col2']) #Col1列和Col2的相关系数
0.6291987738605038

3.数据清洗

数据清洗是数据预处理的最后一道程序,目的是过滤或修改不符合要求的数据

3.1.缺失值处理

缺失值有三种方法处理

3.1.1.删除

如果简单删除一小部分数据能够达到既定目标,那么删除缺失值是最有效的方法.

但删除也有较大的局限性,该方法是以减少历史数据换取数据的完备的,这样会造成资源的大量浪费,丢弃大量隐藏在这些数据中的信息.如果原始数据集包含的样本比较少,那么删除少量的样本就可能对结果产生巨大影响

3.1.2.数据插补

机器学习中的数据插补方法较多这里介绍以下几种

分段线性插补法:https://blog.csdn.net/qq_35166974/article/details/90115563

拉格朗日插值法:根据数学知识可以直到,对于不在一条直线上的n个点,可以找到一个n-1次多项式,使此多项式的曲线穿过这n个点,再将缺失的函数值对应的点x插入多项式得到近似值y.拉格朗日插值法多项式结构紧凑,在理论分析中非常方便,但是当插值的结点增加时,多项式就会随之变化,为克服这一缺点提出了牛顿插值法

牛顿插值法:https://baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E6%8F%92%E5%80%BC%E5%85%AC%E5%BC%8F/18880731?fr=aladdin

3.1.3.不处理

如果缺失值的特征不重要,不会进入后续的建模步骤,或者算法自身能够处理缺失的情况(如随机森林),这种情况不需要对缺失值有任何处理.这种做法的缺点是在算法的选择上有局限

Python中的缺失值插补方法有

DataFrame.fillna():将缺失值用指定值替换

DataFrame.interpolate():用指定的方法插补空值,默认用分段线性插补法

DataFrame.dropna():删除对象中的空值

>>> # s为列向量，n为缺失值位置，取缺失值前后k个数据，默认为5
... def ployinterp_column(s, n, k=5):
...   y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))]  # 取数
...   y = y[y.notnull()] #剔除空值
...   return lagrange(y.index, list(y))(n)  # 插值并返回插值结果
... 
>>> data
    extra
0     0.7
1    -1.6
2    -0.2
3    -1.2
4    -0.1
5     3.4
6     3.7
7     0.8
8     NaN
...
19    3.4
>>> for j in data.index:
...     if (data['extra'].isnull())[j]: #如果为空即插值。
...         data['extra'][j] = ployinterp_column(data['extra'], j)
... 
>>> data
       extra
0   0.700000
1  -1.600000
2  -0.200000
3  -1.200000
4  -0.100000
5   3.400000
6   3.700000
7   0.800000
8   0.372619
...
19  3.400000

3.2.异常值处理

异常值是否需要剔除需要视具体情况而定,因为有些异常值可能蕴含着有用的信息.异常值有三种常见方法处理:

删除含有异常值的记录:直接将含有异常值的记录删除,在观测值很少时,可能使分析不准确

视为缺失值:将异常值视为缺失值,用缺失值处理的方法处理

不处理:直接在有异常值的数据集上进行模型训练

在很多情况下,要先分析异常值出现的可能原因,再选择异常值的处理方法

4.数据合并

数据合并即将不同的有关联性的数据合并在同一张表中

4.1.数据堆叠

数据堆叠就是简单地把两张表拼在一起,也称轴向连接,绑定或堆叠,可以使用Python的concat实现

>>> data1=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\childhood-lead1.csv',index_col=0)
>>> data2=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\childhood-lead2.csv',index_col=0)
>>> data1
      Population  Children   number
2005      360396      19043     260
2006      365075      31961     345
2007      370240      36428     269
2008      374378      39174     243
2009      377117      19493     204
2010      365443      17088     122
>>> data2
      Population  number     ratio
2005      360396     260  0.013700
2007      370240     269  0.007384
2009      377117     204  0.010500
2011      363869     119  0.005325
2013      356565     119  0.004011
2015      354230     101  0.004633
>>> sheet_in=pd.concat([data1,data2],axis=1,join='inner')
>>> sheet_out=pd.concat([data1,data2],axis=1,join='outer')
>>> sheet_in
      Population  Children   number  Population  number     ratio
2005      360396      19043     260      360396     260  0.013700
2007      370240      36428     269      370240     269  0.007384
2009      377117      19493     204      377117     204  0.010500
>>> sheet_out
      Population  Children   number  Population  number     ratio
2005    360396.0    19043.0   260.0    360396.0   260.0  0.013700
2006    365075.0    31961.0   345.0         NaN     NaN       NaN
2007    370240.0    36428.0   269.0    370240.0   269.0  0.007384
2008    374378.0    39174.0   243.0         NaN     NaN       NaN
2009    377117.0    19493.0   204.0    377117.0   204.0  0.010500
2010    365443.0    17088.0   122.0         NaN     NaN       NaN
2011         NaN        NaN     NaN    363869.0   119.0  0.005325
2013         NaN        NaN     NaN    356565.0   119.0  0.004011
2015         NaN        NaN     NaN    354230.0   101.0  0.004633

如果要实现纵向堆叠的两张表列名完全一致,也可以使用append方法实现堆叠,基本语法格式为

DataFrame.append(self,other,ignore_index=None,verify_integrity=False)

other:接收DataFrame或Series,表示要添加的新数据,无默认

ignore_index:接收bool,若输入为True,则会对新生成的DataFrame使用新的索引(自动产生)而忽略原来数据的索引,默认为False

verify_integrity:接收bool,若输入为True,则当ignore_index为Fasle时,会检查添加的数据索引是否冲突,若冲突,则会添加失败,默认为Fasle

>>> sheet_in0=pd.concat([data1,data2],axis=0,join='inner')
>>> sheet_out0=pd.concat([data1,data2],axis=0,join='outer')
>>> sheet_in0
      Population  number
2005      360396     260
2006      365075     345
2007      370240     269
2008      374378     243
2009      377117     204
2010      365443     122
2005      360396     260
2007      370240     269
2009      377117     204
2011      363869     119
2013      356565     119
2015      354230     101
>>> sheet_out0
      Children   Population  number     ratio
2005    19043.0      360396     260       NaN
2006    31961.0      365075     345       NaN
2007    36428.0      370240     269       NaN
2008    39174.0      374378     243       NaN
2009    19493.0      377117     204       NaN
2010    17088.0      365443     122       NaN
2005        NaN      360396     260  0.013700
2007        NaN      370240     269  0.007384
2009        NaN      377117     204  0.010500
2011        NaN      363869     119  0.005325
2013        NaN      356565     119  0.004011
2015        NaN      354230     101  0.004633
>>> sheet_append=data1.append(data2)
>>> sheet_append
      Children   Population  number     ratio
2005    19043.0      360396     260       NaN
2006    31961.0      365075     345       NaN
2007    36428.0      370240     269       NaN
2008    39174.0      374378     243       NaN
2009    19493.0      377117     204       NaN
2010    17088.0      365443     122       NaN
2005        NaN      360396     260  0.013700
2007        NaN      370240     269  0.007384
2009        NaN      377117     204  0.010500
2011        NaN      363869     119  0.005325
2013        NaN      356565     119  0.004011
2015        NaN      354230     101  0.004633

4.2.主键合并

主键合并即使用一个或多个键将两个表的行连接起来

pandas中的merge和join均可以实现主键合并

>>> data1=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\inpatientCharges1.csv',encoding='gbk')
>>> data2=pd.read_csv('C:\\Users\\PC\\Desktop\\Two\\data\\inpatientCharges2.csv',encoding='gbk')
>>> data1
     Provider Id        ...          Total Discharges 
0          10001        ...                         91
1          10005        ...                         14
2          10006        ...                         24
3          10011        ...                         25
4          10016        ...                         18
5          10023        ...                         67
...
999       490021        ...                         35

[1000 rows x 4 columns]
>>> data2
     Provider Id            ...            Average Medicare Payments
0          10001            ...                           $4,763.73 
1          10005            ...                           $4,976.71 
2          10006            ...                           $4,453.79 
3          10011            ...                           $4,129.16 
4          10016            ...                           $4,851.44 
5          10023            ...                           $5,374.14 
...
999       490021            ...                           $4,879.20 

[1000 rows x 4 columns]
>>> sheet=pd.merge(data1,data2,left_on='Provider Id',right_on='Provider Id')
>>> sheet
     Provider Id            ...            Average Medicare Payments
0          10001            ...                           $4,763.73 
1          10005            ...                           $4,976.71 
2          10006            ...                           $4,453.79 
3          10011            ...                           $4,129.16 
4          10016            ...                           $4,851.44 
...
999       490021            ...                           $4,879.20
[1000 rows x 7 columns]

二、特征工程

机器学习所使用的数据和特征决定了机器学习算法构建的模型的上限,更好的特征能够训练出更好的结果.特征工程是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好作用的过程

1.特征变换

为了使建立的模型更加简单精确,需要对原始数据进行特征变换,把原始的特征转化为更有效的特征.常用的特征变换有以下几种

1.1.标准化

不同特征之间具有不同的量纲,由此造成的数值差异可能很大,为了消除特征之间量纲或取值范围的影响,需要对数据进行标准化处理

离差标准化: $X^*=\frac{x-min(x)}{max(x)-min(x)}$ ,将原始数据映射到[0,1]内,受离群点影响较大,适用于分布均匀的数据

标准差标准化: $X^*=\frac{x-x̄}{σ}$ ,经过该方法处理的数据均值为0,标准差为1,是目前使用最广泛的标准化方法

小数定标标准化: $X^*=\frac{x}{10^k}$ ,k是数据最大值的位数,此处理将所有数据映射到[-1,1]

>>> data=pd.read_csv('C:\\Users\\PC\Desktop\\Three\\data\\swiss.csv',encoding='gbk')
>>> data
              省份  生育能力  农业男性百分比  军队最高教育水平百分比  小学以上教育百分比  天主教百分比  婴儿死亡率  类别
0     Courtelary  80.2     17.0           15         12    9.96   22.2   1
1       Delemont  83.1     45.1            6          9   84.84   22.2   2
2   Franches-Mnt  92.5     39.7            5          5   93.40   20.2   2
3        Moutier  85.8     36.5           12          7   33.77   20.3   1
4     Neuveville  76.9     43.5           17         15    5.16   20.6   1
5     Porrentruy  76.1     35.3            9          7   90.57   26.6   2
...
46   Rive Gauche  42.8     27.7           22         29   58.33   19.3   0
>>> data=data.iloc[:,1:10]   #省份列不是数字,需要剔除
>>> data
    生育能力  农业男性百分比  军队最高教育水平百分比  小学以上教育百分比  天主教百分比  婴儿死亡率  类别
0   80.2     17.0           15         12    9.96   22.2   1
1   83.1     45.1            6          9   84.84   22.2   2
2   92.5     39.7            5          5   93.40   20.2   2
3   85.8     36.5           12          7   33.77   20.3   1
4   76.9     43.5           17         15    5.16   20.6   1
5   76.1     35.3            9          7   90.57   26.6   2
...
46  42.8     27.7           22         29   58.33   19.3   0
>>> def MaxMinScale(data):
...     m_scale=(data-data.min())/(data.max()-data.min())
...     return m_scale
>>> data_m_scale=MaxMinScale(data)
>>> data_m_scale
        生育能力   农业男性百分比  军队最高教育水平百分比  小学以上教育百分比    天主教百分比     婴儿死亡率   类别
0   0.786087  0.178531     0.352941   0.211538  0.079816  0.721519  0.5
1   0.836522  0.496045     0.088235   0.153846  0.845069  0.721519  1.0
2   1.000000  0.435028     0.058824   0.076923  0.932550  0.594937  1.0
3   0.883478  0.398870     0.264706   0.115385  0.323148  0.601266  0.5
4   0.728696  0.477966     0.411765   0.269231  0.030761  0.620253  0.5
5   0.714783  0.385311     0.176471   0.115385  0.903628  1.000000  1.0
...
46  0.135652  0.299435     0.558824   0.538462  0.574144  0.537975  0.0
>>> def StandScale(data):
...     s_scale=(data-data.mean())/(data.std())
...     return s_scale
... 
>>> data_s_scale=StandScale(data)
>>> data_s_scale
        生育能力   农业男性百分比  军队最高教育水平百分比    ...       天主教百分比     婴儿死亡率        类别
0   0.805131 -1.482068    -0.186686    ...    -0.747727  0.775037 -0.242633
1   1.037285 -0.244794    -1.314805    ...     1.047748  0.775037  1.182834
2   1.789785 -0.482562    -1.440152    ...     1.253000  0.088388  1.182834
3   1.253428 -0.623462    -0.562726    ...    -0.176810  0.122720 -0.242633
4   0.540955 -0.315244     0.064007    ...    -0.862821  0.225718 -0.242633
5   0.476913 -0.676299    -0.938766    ...     1.185142  2.285664  1.182834
...
46 -2.188858 -1.010935     0.690739    ...     0.412090 -0.220604 -1.668099

[47 rows x 7 columns]
>>> def DecimaScale(data):
...     k=np.ceil(np.log10(data.abs().max()))
...     d_scale=data/(10**k)
...     return d_scale
... 
>>> data_d_scale=DecimaScale(data)
>>> data_d_scale
     生育能力  农业男性百分比  军队最高教育水平百分比  小学以上教育百分比  天主教百分比  婴儿死亡率   类别
0   0.802    0.170         0.15       0.12  0.0996  0.222  0.1
1   0.831    0.451         0.06       0.09  0.8484  0.222  0.2
2   0.925    0.397         0.05       0.05  0.9340  0.202  0.2
3   0.858    0.365         0.12       0.07  0.3377  0.203  0.1
4   0.769    0.435         0.17       0.15  0.0516  0.206  0.1
5   0.761    0.353         0.09       0.07  0.9057  0.266  0.2
...
46  0.428    0.277         0.22       0.29  0.5833  0.193  0.0

函数转化:使用数学函数对原始数据进行转换,改变原始数据的特征,使特征变得更适合建模.常用来将不具有正态分布的数据转化成具有正态分布的数据,简单的对数变换或者差分运算常常可以将非平稳序列转换成平稳序列;反正切函数转换(X*=2arctan(x)/Π)可以使原始数据落到[-1,1]

>>> data=pd.read_csv('C:\\Users\\PC\Desktop\\Three\\data\\swiss.csv',encoding='gbk')
>>> data=data.iloc[:,1:7]
>>> def LogNorm(data):
...     l_norm=np.log10(data)
...     return l_norm
... 
>>> data_l_norm=LogNorm(data)
>>> data_l_norm
        生育能力   农业男性百分比  军队最高教育水平百分比  小学以上教育百分比    天主教百分比     婴儿死亡率
0   1.904174  1.230449     1.176091   1.079181  0.998259  1.346353
1   1.919601  1.654177     0.778151   0.954243  1.928601  1.346353
2   1.966142  1.598791     0.698970   0.698970  1.970347  1.305351
3   1.933487  1.562293     1.079181   0.845098  1.528531  1.307496
4   1.885926  1.638489     1.230449   1.176091  0.712650  1.313867
5   1.881385  1.547775     0.954243   0.845098  1.956984  1.424882
...
46  1.631444  1.442480     1.342423   1.462398  1.765892  1.285557
>>> def TanNorm(data):
...     t_norm=pd.DataFrame(np.zeros([len(data),len(data.columns)]))
...     for i in range(len(data)):
...         for j in range(len(data.columns)):
...             t_norm.iloc[i,j]=math.atan(data.iloc[i,j])*2/np.pi
...     return t_norm
... 
>>> data_t_norm=TanNorm(data)
>>> data_t_norm
           0         1         2         3         4         5
0   0.992063  0.962595  0.957621  0.947071  0.936296  0.971343
1   0.992339  0.985887  0.894863  0.929553  0.992497  0.971343
2   0.993118  0.983968  0.874334  0.874334  0.993184  0.968510
3   0.992581  0.982563  0.947071  0.909666  0.981154  0.968665
4   0.991722  0.985368  0.962595  0.957621  0.878135  0.969120
5   0.991635  0.981970  0.929553  0.909666  0.992971  0.976078
...
46  0.985128  0.977027  0.971083  0.978056  0.989087  0.967044

1.2.独热编码

机器学习中常常遇到类型数据,如性别分为男和女,手机运营商分为移动,联通和电信.这种情况可以使用独热编码处理

独热编码又称一位有效编码,是处理类型数据较好的方法.主要是使用N位状态寄存器来对N个状态进行编码,每个寄存器都有它独立的寄存器位,并且再任意时刻都只有一个编码位有效,对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征,并且这些特征是互斥的,每一次都只有一个被激活,这时原来的数据经过独热编码后就会编程稀疏矩阵.独热编码的优点有:

1.将离散型特征的取值扩展到了欧氏空间,离散型特征的某个取值对应欧式空间的某个点

2.对离散型特征使用独热编码后,会让特征之间的距离计算更为合理

>>> from sklearn import preprocessing
>>> enc=preprocessing.OneHotEncoder()
>>> m=[[0,0,3],[1,2,0],[0,1,1],[1,0,2]]
>>> m
[[0, 0, 3], [1, 2, 0], [0, 1, 1], [1, 0, 2]]
>>> enc.fit(m)
OneHotEncoder(categorical_features='all', dtype=<class 'numpy.float64'>,
       handle_unknown='error', n_values='auto', sparse=True)
>>> enc.transform([[0,0,0]]).toarray()
array([[1., 0., 1., 0., 0., 1., 0., 0., 0.]])
>>> enc.transform([[0,1,2]]).toarray()
array([[1., 0., 0., 1., 0., 0., 0., 1., 0.]])
>>> enc.transform([[1,2,3]]).toarray()
array([[0., 1., 0., 0., 1., 0., 0., 0., 1.]])

这里OneHotEncoder类使用的训练集为[[0,0,3],[1,2,0],[0,1,1],[1,0,2]],每一列代表一个属性,独热编码时对应一个属性的单独编码,如第一列只有0和1两个数值,此时0的编码为10,1的编码为01,而且不论数值排列顺序如何,独热编码时均按照从小到大的顺序排列,即数字较大的先编码,在[[1,2,3]]独热编码后的前两位(0,1)对1编码,(0,0,1)对2编码,(0,0,0,1)对3编码

1.3.离散化

离散化是指将连续型特征(数值型)转换为离散型特征(类别型)的过程,需要在数据的取值范围内设定若干离散的划分点,将取值范围划分为一系列区间,最后用不同的符号或标签代表每个子区间.

部分只能接收离散型数据的算法,需要将数据离散化后才能正常运行,使用离散化与独热编码搭配的方法,还能够降低数据的复杂度,将其变得稀疏,增加算法的运行速度,常用的离散化方法如下

1.3.1.等宽法

等宽法是将数据的值域分成具有相同宽度区间的离散化方法,区间的个数由数据本身的特定或用户确定.pandas的cut函数可以完成此工作

>>> data=pd.read_csv('C:\\Users\\PC\Desktop\\Three\\data\\swiss.csv',encoding='gbk')
>>> data=data.iloc[:,1:7]
>>> sepal=pd.cut(data.iloc[:,5],3)
>>> sepal
0       (21.333, 26.6]
1       (21.333, 26.6]
2     (16.067, 21.333]
3     (16.067, 21.333]
4     (16.067, 21.333]
5       (21.333, 26.6]
6       (21.333, 26.6]
7       (21.333, 26.6]
8     (16.067, 21.333]
...
Name: 婴儿死亡率, dtype: category
Categories (3, interval[float64]): [(10.784, 16.067] < (16.067, 21.333] < (21.333, 26.6]]
>>> sepal.value_counts()
(16.067, 21.333]    32
(21.333, 26.6]      12
(10.784, 16.067]     3
Name: 婴儿死亡率, dtype: int64

等宽离散化要求数据分布均匀,否则会严重损坏建立的模型

1.3.2.等频法

等频法是将相同数量的记录放在每个区间的离散化方法,能够保证每个区间的数量基本一致

>>> data=pd.read_csv('C:\\Users\\PC\Desktop\\Three\\data\\swiss.csv',encoding='gbk')
>>> data=data.iloc[:,1:7]
>>> def SameRateCut(data,k):
...     w=data.quantile(np.arange(0,1+1/k,1/k))
...     data=pd.cut(data,w)
...     return data
... 
>>> result=SameRateCut(data.iloc[:,5],3).value_counts()
>>> result
(20.8, 26.6]      16
(18.967, 20.8]    15
(10.8, 18.967]    15
Name: 婴儿死亡率, dtype: int64
>>> data.quantile(np.arange(0,1+1/3,1/3))       #quantile在这里可以产生0,1/3,2/3,1的分位数
               生育能力    农业男性百分比    ...          天主教百分比      婴儿死亡率
0.000000  35.000000   1.200000    ...        2.150000  10.800000
0.333333  65.433333  40.966667    ...        6.640000  18.966667
0.666667  75.900000  63.366667    ...       76.003333  20.800000
1.000000  92.500000  89.700000    ...      100.000000  26.600000

[4 rows x 6 columns]
>>> np.arange(0,1+1/3,1/3)
array([0.        , 0.33333333, 0.66666667, 1.        ])

等频法虽然避免了类分布不均匀的问题,但同时也可能将数值非常接近的两个值分到不同的区间以满足每个区间的数量相等

1.3.3.基于聚类分析的方法

基于聚类分析的方法是将连续型数据用聚类算法(如K-Means算法等)进行聚类,然后通过聚类得到的簇对数据进行离散化的方法,合并到一个簇的连续型数据为一个区间.基于聚类分析的方法需要用户指定簇的个数,用来决定产生的区间数

>>> data=pd.read_csv('C:\\Users\\PC\Desktop\\Three\\data\\swiss.csv',encoding='gbk')
>>> data=data.iloc[:,1:7]
>>> def KmeanCut(data,k):
...     from sklearn.cluster import KMeans
...     kmodel=KMeans(n_clusters=k,n_jobs=3)
...     kmodel.fit(data.reshape(len(data),1))
...     c=pd.DataFrame(kmodel.cluster_centers_).sort_values(0)
...     w=c.rolling(2).mean()
...     w=pd.DataFrame([0]+list(w[0])+[data.max()])
...     w.fillna(value=c.min(),inplace=True)
...     w=list(w.iloc[:,0])
...     data=pd.cut(data,w)
...     return data 
>>> result=KmeanCut(np.array(data.iloc[:,5]),3).value_counts()
>>> result
(0.0, 15.286]       2
(15.286, 17.42]     5
(17.42, 21.56]     28
(21.56, 26.6]      12
dtype: int64

基于K-Means算法进行聚类分析的离散化方法可以根据现有数据的分布状况进行聚类,但是由于K-Means算法本身的缺陷,用该方法进行离散化时依旧需要指定离散化后类别的数目.此时需要配合聚类算法评价方法,找出最优的聚类簇数目

2.特征选择

特征选择也称特征子集选择,是从原始特征中选择出一些最有效的特征以降低数据维度的过程,是提高机器学习算法性能的一个重要手段.特征选择能够剔除不相关或者冗余的特征,从而达到减少特征个数,提高模型精确度,减少运行时间的目的

2.1.子集搜索与评价

子集搜索法在原始特征中选择出最优的特征子集,避免特征过多时遇到指数爆炸问题,该方法在选择特征时采取从候选特征子集中不断迭代生成更优候选子集的方法,使得的时间复杂度大大减小.该方法主要涉及如何生成候选子集和如何评价候选子集的好坏两个环节

生成候选子集可以使用贪心算法,主要分为以下三种策略:

前向搜索:初始将每个特征视为一个候选子集,然后从当前所有候选子集中选择出最佳的候选子集;接着在上一轮中选出的特征子集中添加一个新的特征,同样选出最佳特征子集,直至选不出比上一轮更好的特征子集

后向搜索:初始将所有特征视为一个候选特征子集,接着尝试剔除上一轮特征子集中一个特征并选出当前最优特征子集,直至选不出比上一轮更好的特征子集

双向搜索:将前向搜索和后向搜索结合起来,即在每一轮中都有添加操作和剔除特征

在选择候选子集时,可以利用信息增益对特征子集的好坏进行评价

2.2.过滤式选择

过滤式选择先对数据集进行特征选择,然后对学习器进行训练,特征的选择与后续学习器无关.Relief方法是一种著名的过滤式特征选择方法,该方法设计了一个"相关统计量"来度量特征的重要性,该统计量是一个向量,其每个分量分别对应一个初始特征,其重要性取决于相关统计量分量之和,详见 https://www.cnblogs.com/asxinyu/p/3289682.html#autoid-2-0-0

除了Relief方法外,方差选择法,相关系数法,卡方检验和互信息法等也是较为常用的过滤式选择方法

2.3.包裹式选择

与过滤式选择不同,包裹式选择在选择特征的同时,将后续的学习器作为特征选择的评价标准.包裹式选择根据目标函数,每次选择若干特征或排除若干特征.这一方法的核心思想是基于某一种模型,宾格给定模型评价方法,针对特征空间中的不同特征子集,计算子集的预测效果,预测效果最好的就是最优特征子集.包裹式选择可以视为为某种学习器量身定做的特征选择方法,由于在每一轮迭代中都需要训练学习器,因此在获得较好性能的同时也产生了较大的开销

LVW算法和RFE算法是较为经典的两种包裹式选择方法

LVW 算法见 https://www.bookstack.cn/read/Vay-keen-Machine-learning-learning-notes/spilt.3.12.md

RFE 算法见 http://www.minxueyu.com/2020/03/29/RFE%E4%B8%8ERFECV%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0/

2.4.嵌入式选择与L1范数正则化

与包裹式选择使用学习器作为特征选择的评价标准不同,嵌入式选择将特征选择的过程与选择器的训练过程融为一体.

详见 https://www.bookstack.cn/read/Vay-keen-Machine-learning-learning-notes/spilt.4.12.md

2.5.稀疏表示与字典学习

"稀疏性"可以理解为在数据集中存在很多0元素,这些0元素并不是以整行或整列形式存在的.当数据集具有稀疏性时,对学习任务会有很多好处,详见 https://www.bookstack.cn/read/Vay-keen-Machine-learning-learning-notes/spilt.5.12.md

>>> from sklearn.feature_selection import SelectKBest
>>> from sklearn.feature_selection import chi2
>>> data=pd.read_csv('C:\\Users\\PC\Desktop\\Three\\data\\swiss.csv',encoding='gbk')
>>> X=data.iloc[:,1:7]
>>> y=data.iloc[:,7]
>>> data
              省份  生育能力  农业男性百分比  军队最高教育水平百分比  小学以上教育百分比  天主教百分比  婴儿死亡率  类别
0     Courtelary  80.2     17.0           15         12    9.96   22.2   1
1       Delemont  83.1     45.1            6          9   84.84   22.2   2
2   Franches-Mnt  92.5     39.7            5          5   93.40   20.2   2
3        Moutier  85.8     36.5           12          7   33.77   20.3   1
4     Neuveville  76.9     43.5           17         15    5.16   20.6   1
5     Porrentruy  76.1     35.3            9          7   90.57   26.6   2
...
46   Rive Gauche  42.8     27.7           22         29   58.33   19.3   0
>>> X
    生育能力  农业男性百分比  军队最高教育水平百分比  小学以上教育百分比  天主教百分比  婴儿死亡率
0   80.2     17.0           15         12    9.96   22.2
1   83.1     45.1            6          9   84.84   22.2
2   92.5     39.7            5          5   93.40   20.2
3   85.8     36.5           12          7   33.77   20.3
4   76.9     43.5           17         15    5.16   20.6
5   76.1     35.3            9          7   90.57   26.6
...
46  42.8     27.7           22         29   58.33   19.3
>>> y
0     1
1     2
2     2
3     1
4     1
5     2
...
46    0
Name: 类别, dtype: int64
#过滤式选择
>>> X_new=SelectKBest(chi2,k=5).fit_transform(X,y)
>>> X_new
array([[ 80.2 ,  17.  ,  15.  ,  12.  ,   9.96],
       [ 83.1 ,  45.1 ,   6.  ,   9.  ,  84.84],
		...
       [ 44.7 ,  46.6 ,  16.  ,  29.  ,  50.43],
       [ 42.8 ,  27.7 ,  22.  ,  29.  ,  58.33]])
>>> X_new.shape
(47, 5)
>>> X.shape
(47, 6)
#包裹式选择
>>> from sklearn.feature_selection import RFE
>>> from sklearn.linear_model import LinearRegression
>>> names=X.columns
>>> names
Index(['生育能力', '农业男性百分比', '军队最高教育水平百分比', '小学以上教育百分比', '天主教百分比', '婴儿死亡率'], dtype='object')
>>> lr=LinearRegression()
>>> rfe=RFE(lr,n_features_to_select=1)
>>> rfe.fit(X,y)
RFE(estimator=LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False),
  n_features_to_select=1, step=1, verbose=0)
>>> sorted(zip(map(lambda x:round(x,5),rfe.ranking_),names))
[(1, '生育能力'), (2, '小学以上教育百分比'), (3, '天主教百分比'), (4, '农业男性百分比'), (5, '婴儿死亡率'), (6, '军队最高教育水平百分比')]
#嵌入式选择
>>> from sklearn.svm import LinearSVC
>>> from sklearn.feature_selection import SelectFromModel
>>> lsvc=LinearSVC(C=0.01,penalty='l1',dual=False).fit(X,y)
>>> model=SelectFromModel(lsvc,prefit=True)
>>> X_new=model.transform(X)
>>> X_new.shape
(47, 5)

三、有监督学习

有监督学习是机器学习中的一类学习算法,这类算法从已经标记好的训练集中学习或建立一个模式,并通过该模式预测新的数据集所对应的结果.训练集由一系列的历史样本构成.每个样本都包含输入对象X和输出对象y.输入对象通常是向量,输出对象包含两种类型:一种是离散的值,即分类的标签;另一种是连续的值.输出对象为分类标签的算法称为分类算法,输出对象为数值的算法称为回归算法

1.有监督学习简介

有监督学习算法多种多样,每种有监督学习算法都有各自的优点和缺点,但是并没有一种有监督学习算法可以解决所有的有监督学习问题.有监督学习算法所构建的模型的效果受数据本身和算法参数的影响较大.数据集在输入时会被转换为特征向量,包含了许多关于描述该输入对象的特征.若特征的数量不够多,则会导致模型的精度不佳,而过多的特征又会造成训练过程过于漫长及过拟合等问题.一些有监督学习算法需要 人工调整参数 才能使模型效果达到一个令人满意的结果,这些参数可以通过测试集或 交叉验证 来进行调整和优化,目前被广泛使用的有监督学习算法有线性回归,逻辑回归,k近邻分类,决策树,支持向量机,朴素贝叶斯和人工神经网络等

需要手动调节的参数叫做超参数，在sklearn中有部分超参数的选择方法

2.度量性能

在有监督学习任务建立模型时,经常会把数据集拆分为训练集和测试集,训练集用于训练模型,调整模型参数,测试集用于验证模型的准确性,所以模型的性能是在测试集上度量的

吴恩达课程学习补充p39-p40

如果实际数据的图形是二次函数，而用一条直线取拟合就会出现欠拟合即高偏差的问题，使用四次函数取拟合则会出现过拟合即高方差的问题过度拟合无法泛化到新的数据中
解决过拟合的方法有两种：首先是尽量减少参数的数量，可以通过人工筛查来判断哪些特征更重要，舍弃不重要的特征即特征选择；第二个方法是正则化，即减少参数的量级，这样使得这些参数达到实际可以舍弃的
正则化的方法是在代价函数中增加正则化项，使得所有参数都尽量减小。 $J(w,b)=\frac{1}{2n}\sum_{i=i}^{n}(h(x^{(i)}-y^{(i)})^2+\lambda\sum_{j=1}^{n}{\theta}_j^2$
$\lambda$ 是正则化参数，作用是平衡“更好地拟合”和“避免过拟合的正则化”两个目标

2.1.分类任务性能度量

2.1.1.正确率和错误率

正确率和错误率是分类任务中最常用的两种性能度量,正确率是指分类正确的样本占总样本的比例,错误率是指分类错误的样本占总样本的比例,更一般地,以二分类任务为例,可以将样本根据真实类别与学习器分类结果的组合划分为真正(TP),假正(FP),真反(TN),假反(FN)四种类型,其中"真"和"假"表示预测与实际是否一致.例如"假反"表示预测为反,实际为正.正确率和错误率分别为

$\frac{TP+TN}{TP+TN+FP+FN}$

$\frac{FP+FN}{TP+TN+FP+FN}$

2.1.2.精确率、召回率和F1度量

正确率和错误率虽然常用,但不能满足所有任务需求.在实际问题中往往关心的是正例样本的分类情况,"精确率"和"召回率"是更适合这类需求的性能度量,其定义分别为

$\frac{TP}{TP+FP}$

$\frac{TP}{TP+FN}$

精确率的含义是"预测结果中为正的样本中有多少实际也为正",召回率的含义是"实际为正的样本中有多是分类结果也为正".精确率和召回率是一对矛盾的度量,一般来说,一种高时另一种偏低,采用 F₁ 度量把两个度量综合起来

$F_1 =\frac{2PR}{P+R}$

在特定的情境下,对精确率和召回率的重视程度不同.例如,在推荐系统中,由于推荐页面的限制,希望在少样本推荐的情况下保证推荐结果是用户感兴趣的,此时精确率更重要;而在车辆是否故障判别过程中,更希望尽量少地漏掉故障车辆,此时召回率更重要.F₁度量的一般形式

$F_{\beta} = \frac{(1+β^2)PR}{β^2P+R}$

其中 β > 0,用于度量精确率和召回率的相对重要性. β=1 时即为F₁度量,此时精确率和召回率有相同的重要性; β<1 时精确率更重要, β>1 召回率更重要

2.1.3.ROC曲线

很多分类器都会对测试样本返回一个分类概率值,然后将这个分类概率值与设定好的概率阈值进行比较,若分类概率值大于概率阈值,则判断为正类,否则判断为反类

ROC曲线也是一种常用的分类器性能度量.ROC曲线是基于真正率(TPR)和假正率(FPR)计算的,二者的计算公式为

$\frac{TP}{TP+FN}$

$\frac{FP}{TN+FP}$

根据概率预测结果,将测试样本进行排序,把概率值大的排在前面,概率值小的排在后面;然后把逐个样本的概率值作为阈值,划分正类和反类,每次都计算得到真正率和假正率的值,这样得到一系列的真正率和假正率,以真正率为纵坐标,假正率为横坐标得到的曲线就是ROC曲线

左上角的 (0,1) 对应所有正例的概率值都比反例高的"理想模型",曲线越靠近左上角说明模型性能越好.可以把ROC量化成一个值进行精确比较,这个值叫AUC,即ROC曲线下的面积.一般AUC取值为 0.5 ~ 1,AUC值越接近1说明模型性能越好

2.2.回归任务性能度量

预测任务最常用的性能度量有均方误差(MES)和均方根误差(RMSE),其计算方式是:

$MSE=\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2$

$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2}$

吴恩达课程学习补充p59

将数据集切分成训练集，交叉验证集和测试集(一般是6:2:2)，多个可能适合的训练集训练好参数后，利用交叉验证集选择代价函数最小的模型，最后用测试集评估模型
如果训练误差和交叉验证误差也较高可能出现了高偏差，即欠拟合；如果训练误差较小，交叉验证误差较大可能出现高方差即过拟合
正则化参数 $\lambda$ 较大可能会出现欠拟合，过小可能会出现过拟合。训练误差和交叉验证误差都较大时， $\lambda$ 过大，训练误差小，交叉验证误差大时， $\lambda$ 过小
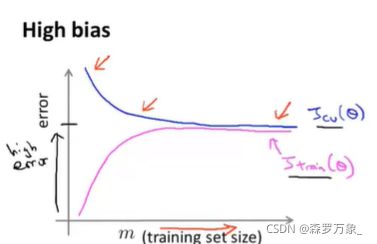
正常的学习曲线如下，从训练样本中切分出部分数据，用于绘制学习曲线。随着样本的增大，正常情况下，训练集的误差增大，交叉验证集的误差减小

当处于高偏差()时，交叉验证集的误差率随着样本数的增大会稍微下降一点，之后马上平缓；训练集的误差增大后平缓，二者在样本数很高时误差几乎一致，都较高。此时增加样本数量并不能起到很好的效果

当处于高方差(过拟合)时，在样本数量较少时，交叉验证集和训练集的误差相差会很大，但随着样本数量的增大，二者的差距会变小。此时增加哦样本数量会有一定的效果

对于以下的措施，有相应的适应情况

措施	情况
获取更多的数据集	高方差（过拟合）
减小 $\lambda$ \ 增大 $\lambda$	高偏差（欠拟合）\ 高方差（过拟合）
减少特征数量 \ 增加特征数量	高方差（过拟合）\ 高偏差（欠拟合）

神经网络较大时，容易过拟合，一般只要添加正则项就可以解决。可以先从小的网络开始一步步增大
在实际面对问题时，先快速实现一个算法，之后通过实际观察错误发生和改进提高性能

3.线性模型

大部分事物的变化都只围绕着均值波动,即大数定理.理论上线性模型可以模拟物理世界中的绝大多数现象.线性模型是对特定变量之间的关系进行建模,分析最常用的手段之一

3.1.线性模型简介

对于有d个属性组成的样本集 x=(x1,x2,x3…,xd),其中xi是x在第i个属性上的取值,线性模型即通过学习得到一个属性的线性组合来预测样本标签的函数,如式 $\hat{y}=wx+b$

3.2.线性回归

对于给定的数据集,要建立一个线性模型预测实际值实际就是要求损失函数值最小时的w和b,即求得

$(w^*,b^*)=argmin_{(w,b)}\sum_{i=1}^n(wx_i+b-y^i)^2$

吴恩达课程学习补充p6-p24,p41和p103

假设函数 $h(x)={\theta}_0+{\theta}_1x_1$ 也就是此处的 $\hat{y}=wx+b$

代价函数 $J(w,b)=\frac{1}{2n}\sum_{i=i}^{n}(h(x^{(i)}-y^{(i)})^2$

代价函数的图像如下,呈碗状,没有局部最优,只有全局最优,因此只要使用梯度下降必定到达最优

梯度下降算法可以解决所求

初始化参数(一般设置为0)
不断改变参数使得代价函数减小直到最小

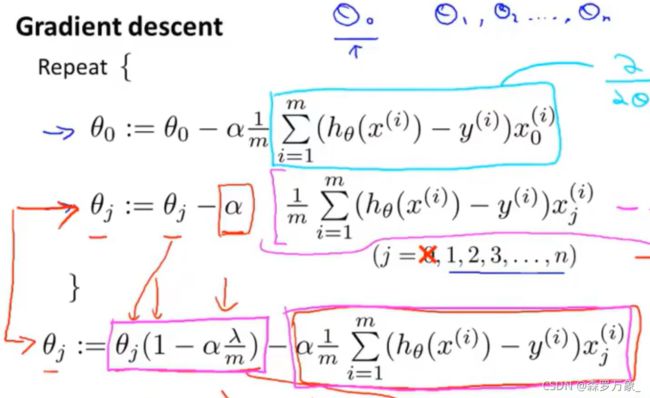
梯度下降算法 https://blog.csdn.net/qq_41800366/article/details/86583789

上面的算法中显示中:

:= 表示赋值,= 表示判断相等
$\alpha$ 表示学习(速)率,它控制算法以多大的幅度更新参数,它永远是一个正数
在算法进行过程中,参数同时更新

线性回归中使用的梯度下降算法也叫 Batch梯度下降算法

多功能梯度下降法

多元线性回归有多个特征向量预测结果，m是样本量，n是样本的维度，即特征的数量
$h(x)={\theta}$ ₁ $x$ ₁+ ${\theta}$ ₀+ ${\theta}$ ₂ $x$ ₂…将x视为向量， $\theta$ 视为参数向量。那么 $h(x)=\theta$ ^Tx
特征缩放：特征的数值相差太大会使得下降时间变长，尤其是再最小值处来回振荡。此时对数据进行标准化能够加速收敛
为了确保算法正确运行，可以画出每步迭代后的代价函数值，判断是否收敛。一般而言，曲线应该呈下降趋势，如果是上升趋势，可能是学习率较大使得下降时不断冲过最低点而到达另一端。只要学习率足够小，它必定下降。
选择能够满足条件的最大的学习率

多项式拟合

将x²看成与x不同的另一个参数，然后视为线性模型拟合。此时需要特别注意具体数值大小

随机梯度下降

随机梯度下降只对单个样本计算梯度值，比批量梯度下降更快，更适合大数据

迷你批量梯度下降

迷你批量梯度下降采用的样本数量是b，介于随机梯度下降和批量梯度下降之间
将b个样本向量化，应用并行计算，速度可能比随机梯度下降更快

监测

使用随机梯度下降或迷你批量梯度下降时，隔n(如1000)个样本计算一次代价函数，做出代价-样本迭代图确定算法实际在收敛

正规方程

增加一个特征x₀=1，将特征数据转化为矩阵X，将结果转换为向量y
$\theta$ =(X^TX)^-1X^Ty 使得参数参数 $\theta$ 最优
正规方程法不需要将数据标准化
(X^TX)^-1可能在实际情况中无法求得，因为X^TX可能不可逆。在一些地方，可以用X^TX的伪逆代替
不可逆的情况往往是因为：包含了多余的特征(不满秩)或样本数太小也可以说特征数太多，如用m=10个样本来拟合n=100个特征

正规方程和梯度下降的对比

梯度下降需要额外确定学习率，且需要迭代；正规方程法不需要
梯度下降法在特征数量n较多时仍然有效；正规方程法慢很多。一般来说，n达到10⁴量级左右是判断标准
正规方程法只是对于线性回归有用，在其他很多算法中，正规方程无效而梯度下降仍然有用

在实际的操作过程中，向量化是一个需要注意的地方。计算 $h(x)={\theta}$ ₁ $x$ ₁+ ${\theta}$ ₀+ ${\theta}$ ₂ $x$ ₂…时，可以直接使用向量内积。将求和转换为向量内积

正则化线性回归

为避免过拟合，在代价函数中增加正则化项，梯度下降方法变成如下形式
正则化正规方程修改为如下形式，它不仅可以避免过拟合，还可以避免矩阵不可逆的情况出现，只要 $\lambda$ 严格大于0，前项必定可逆

使用scikit-learn库中的linear_model模块中的 LinearRegression 类可以建立线性回归模型,具体使用见 https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)

# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]

# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]

# Create linear regression object
regr = linear_model.LinearRegression()

# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)

# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)

# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print('Mean squared error: %.2f'
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.2f'
      % r2_score(diabetes_y_test, diabetes_y_pred))

# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()

多项式回归

model=pipeline.make_pipeline(PolynomialFeatures(2),LinearRegression())
model.fit(X,y)

岭回归(正则化版本的线性回归)

from sklearn.linear_model import Ridge, LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
import matplotlib.pyplot as plt

np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)

def plot_model(model_class, polynomial, alphas, **model_kargs):
    for alpha, style in zip(alphas, ("b-", "g--", "r:")):
        # 岭回归如果alpha为0，就变成了线性回归
        model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression() 
        # 多项式岭回归
        if polynomial:
            model = Pipeline([
                    ("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
                    ("std_scaler", StandardScaler()),
                    ("regul_reg", model),
                ])
        model.fit(X, y)
        y_new_regul = model.predict(X_new)
        lw = 2 if alpha > 0 else 1
        plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))
    plt.plot(X, y, "b.", linewidth=3)
    plt.legend(loc="upper left", fontsize=15)
    plt.xlabel("$x_1$", fontsize=18)
    plt.axis([0, 3, 0, 4])

plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)

plt.show()

在现实场景中,更多的场景是自变量x和因变量y并不是呈线性关系,而是与y的某个函数呈线性关系,此时需要引入广义线性回归模型.见 https://xg1990.com/blog/archives/304

3.3.逻辑回归

吴恩达课程学习补充p32-38和42

逻辑回归LogisticRegression是一种分类算法
$h(x)=g(\theta^Tx)=$ $\frac{1}{1+e^{-z}}=$ $\frac{1}{1+e^{-\theta^Tx}}$
$h(x)=P(y=1|x;\theta)$ 。给定输入特征x和拟合得到的参数 $\theta$ 后，输出的是得到某一结果的估计概率
如果将0.5作为分类界限，那么 $\theta^Tx$ 的正负决定了最终的分类结果。 $\theta^Tx=0$ 表示的是决策边界
在参数中增加多项式可以改变决策边界的形状
像线性回归一样构造代价函数会使得最终结果不是一个凸函数，以至于梯度下降无法达到全局最小值，因此构造以下的函数
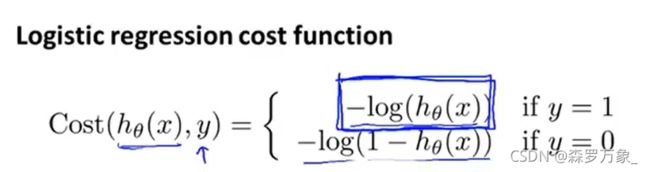
此代价函数在预测值与真实值一致时，代价趋近于0，完全相反时时趋近于无穷
上面的代价函数可以完全等效于 $J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]}$
将代价函数最小化同样可以使用梯度下降，在最后的表达式中，只有 $h (x)$ 不一样
还有很多更高级的优化算法可以使代价函数最小(代价函数的表达可能不同)，例如共轭梯度下降，拟牛顿法等。它们的收敛速度往往比梯度下降更快，但是实现起来更复杂
分别对所有类别进行一对多分类可以拟合出n个逻辑分类器，每一个分类器能够分类其中一种类别，最后输入x后选择合适的分类器

正则化逻辑回归

为避免过拟合，将梯度下降方法的代价函数修改为

对于二分类问题,使用用逻辑回归模型,见 https://zhuanlan.zhihu.com/p/74874291

使用 sklearn.learn_model.LogisticRegression 可以建立逻辑回归模型,使用见 https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html .需要知道的是逻辑回归和线性回归都是广义线性回归的一个特例

>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.preprocessing import StandardScaler
>>> data=pd.read_table('C:\\Users\\PC\\Desktop\\data\\fertility_Diagnosis.txt',sep=',')
>>> data
    进行分析的季节  分析时的年龄  是否患有幼稚病  事故或严重创伤  ...   饮酒频率  吸烟习惯  每天花费在坐的小时数  诊断结果
0     -0.33    0.69        0        1  ...    0.8     0        0.88     0
1     -0.33    0.94        1        0  ...    0.8     1        0.31     1
2     -0.33    0.50        1        0  ...    1.0    -1        0.50     0
3     -0.33    0.75        0        1  ...    1.0    -1        0.38     0
4     -0.33    0.67        1        1  ...    0.8    -1        0.50     1
...

[100 rows x 10 columns]
>>> X=data.iloc[:,:9]
>>> y=data.iloc[:,9]
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>>cancer_data_train,cancer_data_test,cancer_target_train,cancer_target_test=train_test_split(X,y,test_size=0.2)
>>> LR.fit(cancer_data_train,cancer_target_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)
>>> cancer_target_test_pred=LR.predict(cancer_data_test)
>>> num_accu=np.sum(cancer_target_test_pred==cancer_target_test)
>>> num_accu
19
>>> cancer_target_test.shape
(20,)

在20个测试集中预测达到19个,说明模型的分类结果比较理想

4.k近邻分类

k近邻分类是一种常用的常用的监督学习方法。其原理非常简单：对于给定的测试样本，基于指定的距离度量找出训练集中与其最近的k个样本，然后基于这k个“邻居”的信息来进行预测。通常，在分类任务中用的是投票法，即选择k个“邻居”中出现最多的类别标记作为预测结果；在回归任务中使用“平均法”，即取k个邻居的实值输出标记的均值作为预测结果；还可以根据距离远近进行加权投票或加权平均，距离最近的样本平均越大。距离度量一般采用欧氏距离。

与其他学习算法相比，k近邻算法有一个明显的不同之处：接收训练集之后没有显示的训练过程。实际上，它是“懒惰学习”的著名代表，此类学习算法在训练阶段只是把样本保存起来，训练时间为零，待接收到测试样本后再进行处理

使用sklearn库中的neighbors模块的KNeighborsClassifier类可以建立k近邻分类模型，使用见 https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html

>>> model_knn=KNeighborsClassifier(n_neighbors=5)
>>> model_knn.fit(cancer_data_train,cancer_target_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
           weights='uniform')
>>> model_knn.predict(cancer_data_test)
array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
      dtype=int64)
>>> from sklearn.metrics import accuracy_score,confusion_matrix
#准确率为
>>> accuracy_score(cancer_target_test,model_knn.predict(cancer_data_test))
0.9
#混淆矩阵为
>>> confusion_matrix(cancer_target_test,model_knn.predict(cancer_data_test))
array([[18,  1],
       [ 1,  0]], dtype=int64)

5.决策树

决策树是一个预测模型，代表的是对象属性与对象值之间的一种映射关系。决策树可以分为分类树和回归树，分类树的输出是样本的类别，回归树的输出是一个预测值

简介见 https://zhuanlan.zhihu.com/p/30059442

决策数生成的关键在于如何选择中间结点，即如何选择最优的划分属性。一般而言，随着划分的不断进行，希望决策树的分支结点所包含的样本尽量属于同一类，即结点的“纯度”越来越高。样本的预测结果取决于其叶节点中包含的样本情况。对于分类任务，分类结果为叶节点中目标变量的众数；对于回归任务，回归结果为叶节点中目标变量的均值

中间结点的决定即决策树的生成算法有ID3，C4.5，CART等

sklearn的tree模块提供了DecisionTreeClassifier类用于构建决策树分类模型，见 https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html

>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.tree import DecisionTreeClassifier
>>> cancer=load_breast_cancer()
>>> X=cancer['data']
>>> y=cancer['target']
>>> X
array([[1.799e+01, 1.038e+01, 1.228e+02, ..., 2.654e-01, 4.601e-01,
        1.189e-01],
       [2.057e+01, 1.777e+01, 1.329e+02, ..., 1.860e-01, 2.750e-01,
        8.902e-02],
       [1.969e+01, 2.125e+01, 1.300e+02, ..., 2.430e-01, 3.613e-01,
        8.758e-02],
       ...,
       [1.660e+01, 2.808e+01, 1.083e+02, ..., 1.418e-01, 2.218e-01,
        7.820e-02],
       [2.060e+01, 2.933e+01, 1.401e+02, ..., 2.650e-01, 4.087e-01,
        1.240e-01],
       [7.760e+00, 2.454e+01, 4.792e+01, ..., 0.000e+00, 2.871e-01,
        7.039e-02]])
>>> y
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
       0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0,
       1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0,
       ...)
>>> X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=22)
>>> dt_model=DecisionTreeClassifier(criterion='entropy') #entropy表示使用C4.5算法生成决策树
>> dt_model.fit(X_train,y_train)
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=None,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=None,
            splitter='best')
>>> test_pre=dt_model.predict(X_test)
>>> accuracy_score(y_test,test_pre)
0.9385964912280702
>>> confusion_matrix(y_test,test_pre)
array([[38,  5],
       [ 2, 69]], dtype=int64)

CART算法是一种著名的决策树算法，可以用于分类及预测任务

>>> data=pd.read_table('C:\\Users\\PC\\Desktop\\data\\EEG Eye State.arff.txt',sep=',')
>>> X=data.iloc[:,:14]
>>> y=data.iloc[:,14]
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> traindata,testdata,traintarget,testtarget=train_test_split(X,y,test_size=0.2)
>>> model_dtc=DecisionTreeClassifier()
>>> model_dtc.fit(traindata,traintarget)
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=None,
            splitter='best')
>>> targetpre=model_dtc.predict(testdata)
>>> accuracy_score(testtarget,targetpre)
0.8384512683578104
>>> confusion_matrix(testtarget,targetpre)
array([[1388,  235],
       [ 249, 1124]], dtype=int64)

6.支持向量机

支持向量机是一种二分类的有监督学习算法，除可以进行线性分类之外，支持向量机还可以使用核函数有效进行非线性分类，将输入映射到高维特征空间中

6.1支持向量机简介

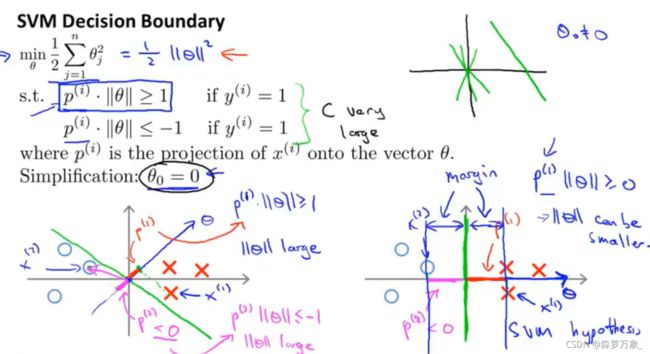
给定数据集，支持向量机(SVM)的思想是在样本空间中找到一个划分超平面，将不同类别的样本划分，划分超平面可以通过线性方程来描述 $w^T+b=0$ 。w是法向量，决定了超平面的方向，b为移位项，决定了超平面与原点之间的距离。SVM的目的就是找到最优的划分超平面

6.2.线性支持向量机

如果存在一条直线能够将两类样本完全分开，则称为线性可分。空间中任意点x到超平面的距离为 $d=\frac{|w^T(x-x')|}{||w||}=\frac{w^Tx+b}{||w||}$

假设超平面能将训练样本正确分类。距离超平面最近的几个样本被称为支持向量，两类异类支持向量到超平面的距离之和称为间隔。找到最优的划分超平面，即找到具有**“最大间隔”的超平面，也就是要找到能满足条件的参数w**和b，即将 w 最小化。支持向量机的数学模型是一个带有不等式约束的最小化问题。

吴恩达课程学习补充p70

支持向量机的代价函数是 $C\sum_{i=1}^m[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum_{i=1}^n{\theta}^2_j$
如果正则化参数 C 较大，它对异常值会更敏感
两类样本之间的距离足够大才会使得参数足够小，因此求得最小化的参数会得到两类样本的最大间隔

6.3.非线性支持向量机

在现实场景中，样本空间很可能补存在一个能正确划分样本的超平面。对于这类问题，有一种解决方法是：将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间线性可分。这里存在一个数学定理：如果原始空间是有限维的，那么一定存在一个高维空间使得样本线性可分。

高斯核函数衡量待预测点和提前设置的标记点的距离，距离远的设置为0，距离近的设置为1，从而在标记点周围形成一个非线性范围来划分类别
高斯核函数中， $\sigma$ 小得到低偏差和高方差， $\sigma$ 大得到高偏差和低方差
当特征数量较大或特征数接近于样本数(用于训练的数据)较少适用于逻辑回归或线性SVM
当特征数量较小时可以适用高斯核函数的SVM
当训练集很大而特征数很小时，高斯核函数SVM会较慢

sklearn库中的svm模块的SVC类可以建立支持向量机模型，见 https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html

>>> from sklearn.svm import SVC
>>> data=pd.read_table('C:\\Users\\PC\\Desktop\\data\\fertility_Diagnosis.txt',sep=',')
>>> X=data.iloc[:,:9]
>>> y=data.iloc[:,9]
>>> X
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> traindata,testdata,traintarget,testtarget=train_test_split(X,y,test_size=0.2)
>>> model_svc=SVC()
>>> model_svc.fit(traindata,traintarget)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)
>>> targetpre=model_svc.predict(testdata)
>>> accuracy_score(testtarget,targetpre)
0.85
>>> confusion_matrix(testtarget,targetpre)
array([[17,  0],
       [ 3,  0]], dtype=int64)

绘制SVM决策边界

def plotBoundary(clf, X):
    """
    :param clf:训练好的SVM模型 
    :param X: 待预测的数据矩阵
    :return: 画出对应数据矩阵的SVM决策边界
    """
    x_min, x_max = X[:, 0].min() * 1.1, X[:, 0].max() * 1.1
    y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
    # meshgrid生成网格点坐标矩阵,给出x轴和y轴上的点,返回对应所有点的坐标矩阵
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
    # np.c_中的c_是column(列)的缩写,就是按列叠加两个矩阵或向量,要求行数相等
    Z = clf.predict(np.c_[xx.flatten(), yy.flatten()])
    Z = Z.reshape(xx.shape)
    plt.contour(xx, yy, Z)

7.朴素贝叶斯

贝叶斯分类算法是一类分类算法的总称,这类算法均以贝叶斯定理为基础,所以统称为贝叶斯分类算法.详见 https://zhuanlan.zhihu.com/p/26262151

在Python中,朴素贝叶斯分类可以利用高斯朴素贝叶斯和多项式朴素贝叶斯算法实现.高斯朴素贝叶斯主要处理连续型变量的数据,它的模型假设是每个维度都符合高斯分布,使用sklearn库中的naive_bayes模块的GaussianNB类可以构建高斯朴素贝叶斯分类模型,使用方法详见 https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html

>>> from sklearn.naive_bayes import GaussianNB
>>> data=pd.read_table('C:\\Users\\PC\\Desktop\\data\\pima-indians-diabetes.data.txt',sep=',')
>>> X=data.iloc[:,:8]
>>> y=data.iloc[:,8]
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
>>> model=GaussianNB()
>>> model.fit(X_train,y_train)
GaussianNB(priors=None)
>>> pre=list(model.predict(X_test))
>>> from sklearn.metrics import accuracy_score
>>> accuracy_score(y_test,pre)
0.7272727272727273

8.神经网络

神经网络能在外界信息的基础上改变内部结构,是一个具备学习动能的自适应系统.与其他机器学习方法一样,神经网络已经被用于解决各种各样的问题,如机器视觉和语音识别

8.1.神经网络介绍

神经网络是由具有适应性的简单单元组成的广泛并行互联网络,它的组织能够模拟生物神经网络系统对真实世界物体所作出的交互反应.这里定义的"简单单元",是指一个神经元模型,它是神经网络中最基本的成分.在生物神经网络中,每个神经元与其他神经元相连,当它"兴奋"时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;若神经元点位超过了某个"阈值",它就会被激活,即"兴奋"起来,向其他神经元发送化学物质

把神经元模型表示成一个数学模型,将输入信号通过带权重的连接进行传递,将神经元接收的总输入值与阈值做比较,然后通过"激活函数"处理以产生神经元的输出,其中激活函数一般采用非线性函数(如Sigmoid函数)多个神经元按一定的层次结构连接起来,就得到神经网络.

更一般的神经网络是下面所示的层级结构,每层神经元与下层高神经元全互联,神经元之间不存在同层连接,也不存在跨层连接

吴恩达课程学习补充p43-p57

在一些问题中，特征数量太多(如机器视觉中的像素点)会导致计算量太大或者是过拟合的问题，使用一般的方法无法很好地解决

${\theta}^{(j)}$ 表示第 j 层的权重矩阵， ${\theta}^{(j)}_{ik}$ 表示的是第 j 层的第 k 个神经元向第 j+1 层的第 i 的神经元的计算权重。如 ${\theta}^{(1)}_{12}$ 表示第1层的第2个神经元向第2层的第1个神经元输入的权重值。这里的“第”不是通常意义的第。
$a^{(2)}=g(z^{(2)})$ ， $z^{(2)}={\theta}^{(1)}x$ 。 $S_j$ 表示的是第 j 层的除偏置项的神经元数量，L 表示总层数
代价函数类似于逻辑回归:
- $J({\theta})=-\frac{1}{m}[\sum_{i=1}^{m}\sum_{k=1}^{k}y_k^{(i)}log(h_{\theta}(x^{(i)}))_k+(1-y_k^{(i)})log(1-h_{\theta}(x^{(i)}))_k]+\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}({\theta_{ji}^{(l)}})^2$

上面的网络结构称为"多层前馈神经网络",其中输入层神经元对信号进行加工,最终输出结果由输出层神经元输出;也就是说,输入层神经元只是接收输入,不进行函数处理,隐层与输出层包含功能神经元.神经网络的学习过程,就是根据训练数据来调整神经元之间的"连接权重"及每个神经元的阈值,神经网络"学"到的信息,蕴含在连接权和阈值中.

8.2.BP神经网络

梯度见 https://blog.csdn.net/Cowry5/article/details/80370798

误差值 ${\delta}^{(l)}_j=\frac{\partial}{{\partial}z_j^{(l)}}J(i)$ 也就是代价函数的偏导数
反向传播算法中，输出层的误差向量是 ${\delta}^{(L)}=a^{(L)}-y$ ，隐藏层 k 的误差向量是** ${\delta}^{(k)}=({\theta}^{(k)})^T{\delta}^{(k+1)}.*g'(z^{(k)})=({\theta}^{(k)})^T{\delta}^{(k+1)}.*[a^{(k)}.*(1-a^{(k)})]$ **。
${\delta}$ 也可以写作它的大写形式 ${\varDelta}$
在算法实现出现bug时，bug造成的影响会被成倍放大。使用梯度检测的方法来避免出错
在开始训练前，用上面的式子计算代价函数的偏导数，再通过另一种近似的方法(双侧差分)来计算导数，看二者是否近似

训练多层神经网络一般采用误差逆传播(BP)算法,通常说的"BP神经网络",是指用BP算法训练的多层前馈神经网络

BP算法流程如下

在(0,1)范围内随机初始化网络中所有权值和阈值
将训练样本提供给输入层神经元,然后逐层将信号前传,直到产生输出层的结果,这一步一般称为信号向前传播
计算代价函数
计算输出层误差,将误差逆向传播至隐层神经元,再根据隐层神经元误差来对权值和阈值进行更新,这一步一般称为误差向后传播
将反向传播得到的误差 $\delta$ 与梯度检测得到的估计误差相比较，检测是否存在 bug，如不存在，关闭梯度检测
使用高级的优化算法来最小化代价函数

使用sklearn库中的neural_network模块的MLPClassifier类可以建立神经网络模型,使用方法见 https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html

>>> from sklearn.neural_network import MLPClassifier
>>> data=pd.read_table('C:\\Users\\PC\\Desktop\\data\\pima-indians-diabetes.data.txt',sep=',')
>>> X=data.iloc[:,:8]
>>> y=data.iloc[:,8]
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=123)
>>> model_network=MLPClassifier(hidden_layer_sizes=(20,27))
>>> model_network.fit(X_train,y_train)
MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,
       beta_2=0.999, early_stopping=False, epsilon=1e-08,
       hidden_layer_sizes=(20, 27), learning_rate='constant',
       learning_rate_init=0.001, max_iter=200, momentum=0.9,
       nesterovs_momentum=True, power_t=0.5, random_state=None,
       shuffle=True, solver='adam', tol=0.0001, validation_fraction=0.1,
       verbose=False, warm_start=False)
>>> pre=model_network.predict(X_test)
>>> accuracy_score(y_test,pre)
0.7662337662337663

>>> from sklearn.metrics import roc_curve,auc
>>> import matplotlib.pyplot as plt
>>> fpr,tpr,thresholds=roc_curve(y_test,pre)
>>> AUC=auc(fpr,tpr)
>>> AUC
0.7408405172413793
>>> plt.figure(figsize=(10,6))
<Figure size 1000x600 with 0 Axes>
>>> plt.title("ROC curve")
Text(0.5,1,'ROC curve')
>>> plt.xlabel("FPR")
Text(0.5,0,'FPR')
>>> plt.ylabel("TPR")
Text(0,0.5,'TPR')
>>> plt.plot(fpr,tpr)
[<matplotlib.lines.Line2D object at 0x000002E40B1D8F28>]
>>> plt.show()

9.集成学习

在机器学习中,集成学习算法通过组合使用多种学习算法获得比单独使用任何一种学习算法更好的预测性能.

9.1.Bagging

假设有个病人去医院看病,希望根据医生的诊断进行治理,他可能选择看多个医生,而不是一个;若某种诊断比其他诊断出现的次数更多,则将它作为最终的诊断结果.也就是说最终诊断结果是根据多数表决做出的,每个医生都具有相同的权重.把医生视为分类器,就得到Bagging的思想,单个分类器称为基分类器.直观地,多数分类器的结果比少数分类器的结果更可靠.对于包含n个训练集样本的数据集D,组成的分类器有k个,Bagging的过程如下

1.利用自助法生成k个训练集Di,即每个Di都是从原数据集中有放回地抽取n个样本得到的

2.在每个训练集Di上学习一个分类器Mi

3.最终的分类结果由所有分类器投票所得,即取分类结果最多的类别作为最终的分类结果

随机森林(RF)是Bagging的一个拓展,随机森岭在以决策树位基分类器构建Bagging学习器的基础上,进一步在决策树的训练过程中引入了随机属性选择,与一般的Bagging方法对比,改进的地方由以下两点:

1.每个基分类器都是一颗决策树,一般是CART决策树

2.每个训练集Di除用自助法抽样之外,还进行了随机属性选择,具体做法是在决策树的每个结点,都随机地从可选属性集合(假定有d个属性)中抽取q个属性,再从中选择一个最优属性用于划分,一般令q=log2d

随机森林除拥有Bagging已有的优点之外,还有更加重要的一点:随机森林在每次划分时只考虑很少的属性,因此在大型数据集上效率更高

使用sklearn库中的ensemble模块的RandomForestClassifier类可以建立随机森林模型,使用见 https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html

>>> from sklearn.ensemble import RandomForestClassifier
>>> data=pd.read_table('C:\\Users\\PC\\Desktop\\data\\EEG Eye State.arff.txt',sep=',')
>>> X=data.iloc[:,:14]
>>> y=data.iloc[:,14]
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> traindata,testdata,traintarget,testtarget=train_test_split(X,y,test_size=0.2)
>>> model_rf=RandomForestClassifier()
>>> model_rf.fit(traindata,traintarget)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
            max_depth=None, max_features='auto', max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
            oob_score=False, random_state=None, verbose=0,
            warm_start=False)
>>> pre=model_rf.predict(testdata)
>>> accuracy_score(testtarget,pre)
0.8945260347129506

9.2.Boosting

Boosting是一族可以将弱学习器提升为强学习器的算法.这族算法的工作机制如下:给每个训练样本赋予一个相等的初始权重,迭代地学习k个分类器,学习得到分类器Mi之后,更新权重,使得其后的选择器更关注Mi误分类的训练样本.最终提升的分类器M*组合每个个体分类器的表决,其中每个分类器投票的权重是其准确率的函数.提升算法有 Adaboost,GBM(梯度提升机).GBM算法可以灵活处理各种类型的数据,包括连续值和离散值.相对于SVM来说,它在相对少的调参时间情况下,预测的准备率也可以比较高.GBM算法使用一些健壮的损失函数,对异常值的鲁棒性非常强,例如Huber损失函数和Quantile损失函数.但由于弱学习器之间存在依赖关系,难以并行训练数据,调参和训练消耗的时间较长

使用sklearn库中的ensemble模块的GradientBoostingClassifier类可以建立梯度提升决策树模型,使用见 https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html

>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.datasets import load_wine
>>> wine=load_wine()
>>> data=wine.data
>>> target=wine.target
>>> traindata,testdata,traintarget,testtarget=train_test_split(X,y,test_size=0.2,random_state=1234)
>>> model_gbm=GradientBoostingClassifier()
>>> model_gbm.fit(traindata,traintarget)
GradientBoostingClassifier(criterion='friedman_mse', init=None,
              learning_rate=0.1, loss='deviance', max_depth=3,
              max_features=None, max_leaf_nodes=None,
              min_impurity_decrease=0.0, min_impurity_split=None,
              min_samples_leaf=1, min_samples_split=2,
              min_weight_fraction_leaf=0.0, n_estimators=100,
              presort='auto', random_state=None, subsample=1.0, verbose=0,
              warm_start=False)
>>> pre=model_gbm.predict(testdata)
>>> accuracy_score(testtarget,pre)
0.8207610146862483

LightGBM也是一种提升算法,包含light(轻量级)和GBM两个关键点,是Boosting集合模型中的新进成员.Python中的lightgbm模块的sklearnAPI提供了LGBMRegressor函数构建LightGBM,使用见 https://lightgbm.readthedocs.io/en/latest/pythonapi/lightgbm.LGBMRegressor.html#lightgbm.LGBMRegressor

>>> import lightgbm as lgb
>>> wine=load_wine()
>>> data=wine.data
>>> target=wine.target
>>> traindata,testdata,traintarget,testtarget=train_test_split(X,y,test_size=0.2)
>>> model_gbm=lgb.LGBMRegressor(objective='regression',num_leaves=31,learning_rate=0.05,n_estimators=30)
>>> model_gbm.fit(traindata,traintarget,eval_set=[(traindata,traintarget)])
>>> model_gbm.fit(traindata,traintarget,eval_set=[(traindata,traintarget)],eval_metric='11',early_stopping_rounds=5)
[1]	training's l2: 0.239537
Training until validation scores don't improve for 5 rounds
[2]	training's l2: 0.232242
[3]	training's l2: 0.225388
[4]	training's l2: 0.219196
[5]	training's l2: 0.213569
[6]	training's l2: 0.207944
[7]	training's l2: 0.202948
[8]	training's l2: 0.197665
[9]	training's l2: 0.193153
[10]	training's l2: 0.188363
[11]	training's l2: 0.184643
[12]	training's l2: 0.180557
[13]	training's l2: 0.177104
[14]	training's l2: 0.17358
[15]	training's l2: 0.170166
[16]	training's l2: 0.166749
[17]	training's l2: 0.163664
[18]	training's l2: 0.161067
[19]	training's l2: 0.158209
[20]	training's l2: 0.155685
[21]	training's l2: 0.153113
[22]	training's l2: 0.150714
[23]	training's l2: 0.148451
[24]	training's l2: 0.146201
[25]	training's l2: 0.144073
[26]	training's l2: 0.141956
[27]	training's l2: 0.140141
[28]	training's l2: 0.138217
[29]	training's l2: 0.136518
[30]	training's l2: 0.134575
Did not meet early stopping. Best iteration is:
[30]	training's l2: 0.134575
LGBMRegressor(boosting_type='gbdt', class_weight=None, colsample_bytree=1.0,
       importance_type='split', learning_rate=0.05, max_depth=-1,
       min_child_samples=20, min_child_weight=0.001, min_split_gain=0.0,
       n_estimators=30, n_jobs=-1, num_leaves=31, objective='regression',
       random_state=None, reg_alpha=0.0, reg_lambda=0.0, silent=True,
       subsample=1.0, subsample_for_bin=200000, subsample_freq=0)
>>> pre=model_gbm.predict(testdata,num_iteration=model_gbm.best_iteration_)
>>> pre=np.around(pre)
>>> accuracy_score(testtarget,pre)
0.8234312416555407

9.3.Stacking

当训练集很多时,可以使用Stacking进行集成学习.Stacking的思想是将一系列初级学习器的训练结果作为特征,输入一个次级学习器中,最终的输出结果由次级学习器产生.Stacking先从初始训练集中训练出初级学习器,然后"生成"一个新数据集用于训练次级学习器.在这个新数据集中,初级学习器的输入被视为样本输入特征,而初始样本的标记仍被视为样例标记

四、无监督学习

无监督学习是指使用没有预设标签的数据集,仅仅根据数据本身的分布特征进行分类或分群的学习方法,其目的在于数据压缩,数据可视化,数据去噪或更好地理解数据中的相关性.无监督学习是数据分析的必备技能,降维和聚类都是常用的无监督学习方法

1.无监督学习简介

无监督学习也属于机器学习,与有监督学习最大的区别在于,无监督学习输入的数据集中没有事先标记好的历史范例,需要算法自行从数据中寻找出潜在的规律和规则,自动对输入的数据进行分类和分群.有监督学习算法从数据集中寻找特定的模式用于特定的用途,而无监督学习算法从数据集中揭露数据中潜在的性质与规则,更倾向于理解数据本身

无监督学习的分类效果精度低于有监督学习,但也有一定的优势.在实际应用中,给训练集中的数据贴上标签往往是一个非常耗时的过程,并且要能为数据贴上标签还需要具备有先验知识.使用无监督学习算法从庞大的数据集中找出不同的类别,由人工对这些类别进行标准后再进行后续处理是常见的应用方法.无监督学习算法也可以用于特征的筛选,之后再用于构建分类器的训练.无监督学习的一个典型应用是聚类分析,在聚类过程中,数据依据相似度自动聚成一簇,这个过程不需要人工干预.除聚类外,常见的无监督学习的应用还有关联规则和降维

2.降维

在样本数据的聚类分析时,有时涉及的变量或数据组属性较多,这增加了数据分析的复杂性.降维处理是一种行之有效的降低数据分析复杂性的手段.其核心思想是,通过原来变量组或数据组属性的线性或非线性的重构达到简化数据分析的目的.常见的降维方法由主成分分析(PCA)和核线性变换

吴恩达课程学习补充p81-p82

当特征高度重复时，可以使用降维算法来减小特征数量，可以减小样本所占空间，加速算法
降维实际是将高维样本投影到低维，使用更少的数字表达同样多的信息
降维可以帮助数据可视化。将尽可能多的特征用两个数字表达就可以在二维平面画出来

2.1.PCA

PCA是一种通过降维技术把多个变量化为几个新的综合变量的统计分析方法.新的综合变量是原始变量的线性组合,能够反映原始变量的绝大部分信息,且新的变量之间互不相关

吴恩达课程学习补充p81-p87

PCA 要找到k个向量，当把数据投影到这些向量上时，误差最小。从线性代数讲，就是将数据投影到向量展开的线性子空间中
进行降维算法前先进行均值标准化和特征缩放。假设要把 n 维降到 k 维，先计算协方差矩阵 ${\varSigma}={\frac{1}{m}}\sum_{i=1}^n(x^{(i)})(x^{(i)})^T$ ， $\varSigma$ 是一个n*n 的矩阵，之后对协方差矩阵进行奇异值分解 $[U,S,V]=svd({\varSigma})$ ，矩阵 $U$ 也是 n*n 的矩阵，取出矩阵 $U$ 的前 k 列组成新的矩阵 $U_{reduce}$ ，降维后某一行样本对应的降维后向量 $z^{(i)}=U_{reduce}^Tx^{(i)}$
通过逆运算 $x_{approx}=U_{reduce}z$ 可以得到原先数据 $x$ 的近似 $x_{approx}$ ，实现原始数据的重构即压缩重现
选择投影后的维度 k 可以遵循规则：选择最小的 k 且使得 $\frac{\frac{1}{m}\sum_{i=1}^m||x^{(i)}-x_{approx}^{(i)}||^2}{\frac{1}{m}\sum_{i=1}^m||x^{(i)}||^2}\le0.01$ 成立，即 99% 的方差将会被保留
使用 PCA 降低维度来避免过拟合不是一个好的方法，避免过拟合可以使用正则化
只有运行速度太慢或有其他原因时，才使用 PCA ，大部分情况下不使用 PCA
奇异值分解和PCA降维见 https://www.cnblogs.com/pinard/p/6251584.html

sklearn库中的 decomposition 模块的PCA类可以创建PCA模型,详见 https://scikit-learn.or1g/0.15/modules/generated/sklearn.decomposition.KernelPCA.html

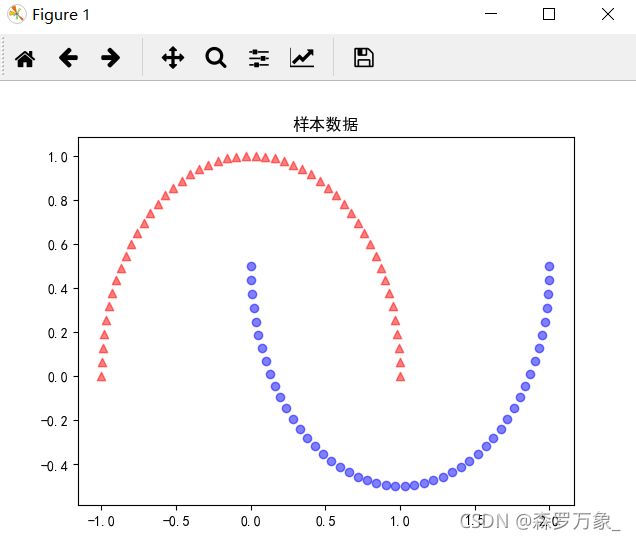
>>> from sklearn.datasets import make_moons
>>> x,y=make_moons(n_samples=100,random_state=233)
>>> plt.scatter(x[y==0,0],x[y==0,1],color='red',marker='^',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C72E5B5C0>
>>> plt.scatter(x[y==1,0],x[y==1,1],color='blue',marker='o',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C72E5B9B0>
>>> plt.rcParams['font.sans-serif']='SimHei'
>>> plt.rcParams['axes.unicode_minus']=False
>>> plt.title('样本数据')
Text(0.5,1,'样本数据')
>>> plt.show()

#用PCA对样本数据进行降维
>>> from sklearn.decomposition import PCA
>>> pca=PCA(n_components=2)
>>> x_pca=pca.fit_transform(x)
>>> fig,ax=plt.subplots(nrows=1,ncols=2,figsize=(7,3))
>>> ax[0].scatter(x_pca[y==0,0],x_pca[y==0,1],color='red',marker='^',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C73678B70>
>>> ax[0].scatter(x_pca[y==1,0],x_pca[y==1,1],color='red',marker='^',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C73678F98>
>>> ax[1].scatter(x_pca[y==0,0],np.zeros((50,1))+0.02,color='red',marker='^',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C73683278>
>>> ax[1].scatter(x_pca[y==1,0],np.zeros((50,1))+0.02,color='blue',marker='o',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C73683780>
>>> ax[0].set_xlabel('X')
Text(0.5,0,'X')
>>> ax[0].set_ylabel('Y')
Text(0,0.5,'Y')
>>> ax[0].set_title('样本数据')
Text(0.5,1,'样本数据')
>>> ax[1].set_ylim([-1,1])
(-1, 1)
>>> ax[1].set_yticks([])
[]
>>> ax[1].set_xlabel('X_pca')
Text(0.5,0,'X_pca')
>>> ax[1].set_title('降维后的样本数据')
Text(0.5,1,'降维后的样本数据')
>>> plt.tight_layout()
>>> plt.show()

2.2.核化线性降维

采用线性降维方法降低数据维度,通常假设从高维空间到低维空间的函数映射是在线性条件下进行的,然而有时高维空间是线性不可分的,需要找到一个非线性函数映射才能进行适当的降维,这就是非线性降维.核化线性降维是非线性降维的常用方法.核主成分分析(KPCA)是一例

sklearn库中的decomposition模块的KernelPCA类可以建立KernelPCA模型,详见 https://scikit-learn.org/stable/auto_examples/decomposition/plot_kernel_pca.html

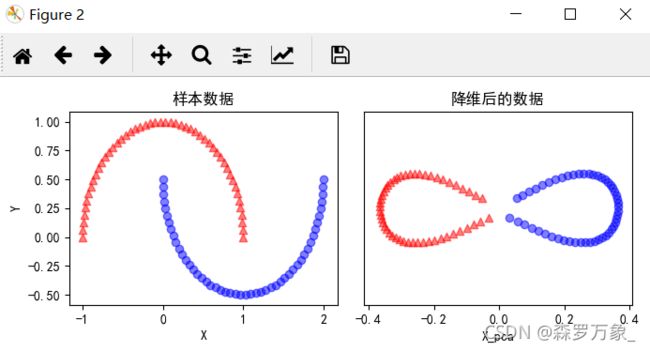
>>> from sklearn.decomposition import KernelPCA
>>> kpca=KernelPCA(n_components=2,kernel='rbf',gamma=15)
>>> x_kpca=kpca.fit_transform(x)
>>> kfig,kx=plt.subplots(nrows=1,ncols=2,figsize=(7,3))
>>> kx[0].scatter(x[y==0,0],x[y==0,1],color='red',marker='^',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C782566A0>
>>> kx[0].scatter(x[y==1,0],x[y==1,1],color='blue',marker='o',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C78256AC8>
>>> kx[1].scatter(x_kpca[y==0,0],x_kpca[y==0,1],color='red',marker='^',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C78256668>
>>> kx[1].scatter(x_kpca[y==1,0],x_kpca[y==1,1],color='blue',marker='o',alpha=0.5)
<matplotlib.collections.PathCollection object at 0x0000012C7825F1D0>
>>> kx[0].set_xlabel('X')
Text(0.5,0,'X')
>>> kx[0].set_ylabel('Y')
Text(0,0.5,'Y')
>>> kx[0].set_title('样本数据')
Text(0.5,1,'样本数据')
>>> kx[1].set_ylim([-1,1])
(-1, 1)
>>> kx[1].set_yticks([])
[]
>>> kx[1].set_xlabel('X_pca')
Text(0.5,0,'X_pca')
>>> kx[1].set_title('降维后的数据')
Text(0.5,1,'降维后的数据')
>>> plt.tight_layout()
>>> plt.show()

3.聚类任务

在无监督学习中,样本的标记信息是未知的,目标是通过对无标记样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础.在此类学习任务中,应用最广泛的就是聚类.

聚类的目的是把待分类的数据按照一定的规则分成若干类,这些类不是事先给定的,而是根据待分类数据的特征确定,且对类的数目和结构不做任何假定.例如,市场分析人员通过聚类将客户分成不同的客户群,以购买模式刻画不同客户群的特征

3.1.聚类性能度量指标

聚类性能度量指标用于衡量聚类结果的优劣.另外,若已明确了聚类性能度量指标,则也可将其作为聚类过程中的优化目标,从而更好地提升聚类效果.当通过一定的聚类算法得到聚类结果之后,通常认为簇内相似度越高越好,而簇间相似度越低越好

若是某个参考模型给出聚类性能度量指标,则这类指标为外部指标,如 Jaccard系数,FM系数,Rand系数,这三个外部指标的计算结果取值为[0,1],取值越大越好;若直接通过考察聚类结果给出聚类性能度量指标,则这类指标称为内部指标,如DB指数(DBI)和Dunn指数(DI),DBI的计算结果越小,表明聚类效果越好,而DI则相反

3.2.距离计算

聚类分析的目的是把分类对象按照一定的规则分成若干类,同一类的对象具有某种相似性,而不同类的对象之间不具有相似性.通常情况下,聚类结果的优劣可以用对象之间距离的远近来评价.在聚类分析中,给定样本点,常用的距离计算公式由欧氏距离,曼哈顿距离,切比雪夫距离,闵文斯基距离,VDM距离

最大最小距离算法是模式识别中一种基于试探的聚类算法,它以欧氏距离为基础,取尽可能远的对象作为聚类中心.因此,它可以避免K-Means算法初值选取时可能出现聚类种子过于临近的情况,它不仅能智能地确定初始聚类种子的个数,而且提高了划分初始数据的效率.

3.3.原型聚类

原型聚类也称为基于原型的聚类,原型聚类算法假设聚类结构能够通过一组原型刻画,在实践操作中极为常用.通常情况下,算法先对原型进行初始化,然后对原型进行迭代更新求解.采用不同的原型表示和不同的求解方式,将产生不同的算法.下面是三种常用的原型聚类算法

3.3.1.K-Means算法

在K-Means算法中,首先随机初始化类的中心,然后将每个样本按照距离最近的原则划分到相应的类内,更新类中心,直到样本到相应类中心的距离平方和达到最小

吴恩达课程学习补充p77-p80

K均值算法通过移动中心和重新分配的迭代达到聚合目标
K均值算法的目标是最小化所有点到其所属的簇类中心距离的平方
随机初始化聚类中心可以选择K个训练样本作为中心
避免局部最优化可以进行多次K均值算法每次选择不同的初始中心，选择代价函数最小的情况。在样本较大时时重复进行算法帮助不大
选择聚类中心的数量有肘部原则，画出不同聚类数量中心的最终代价函数，如果出现了清晰的拐点，可以选择拐点处对应的中心数量
更多使用的选择中心数量的方法是根据下游目标来选择最适合目标的方法

>>> from sklearn.cluster import KMeans
>>> import matplotlib.pyplot as plt
>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\data\\data\\data.csv')
>>> x=data.iloc[:,2:]
>>> y=data.iloc[:,1]
>>> scaler=StandardScaler()
>>> scaler.fit(x)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> x=scaler.transform(x)
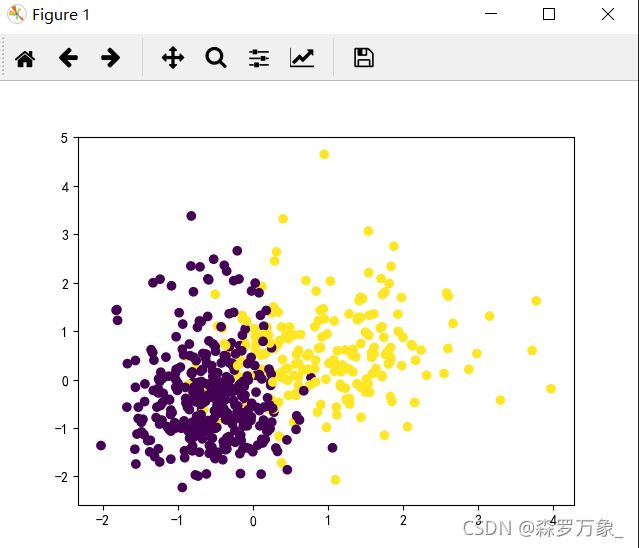
>>> kmeans=KMeans(n_clusters=2,random_state=0).fit(x)
>>> y_pre=kmeans.predict(x)
>>> plt.scatter(x[:,0],x[:,1],c=y)
<matplotlib.collections.PathCollection object at 0x0000012C731189E8>
>>> plt.show()

>>> plt.scatter(x[:,0],x[:,1],c=y_pre)
<matplotlib.collections.PathCollection object at 0x0000012C770244A8>
>>> plt.show()

3.3.2.学习向量量化算法

学习向量量化(LVQ)算法也是一种原型聚类算法.与K-Means算法不同,LVQ算法是假设样本数据是带有标记类型的,通过监督信息来辅助聚类.在LVQ算法中,引入了原型向量的更新学习规则,根据每次迭代中样本与聚类原型的类标记是否相同,针对聚类原型进行更新,直到满足终止条件

import copy
>>> data = pd.read_csv('C:\\Users\\PC\\Desktop\\data\\data\\data.csv')
>>> X=data.iloc[:,2:]
>>> y=data.iloc[:,1].values
>>> #数据标准化
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
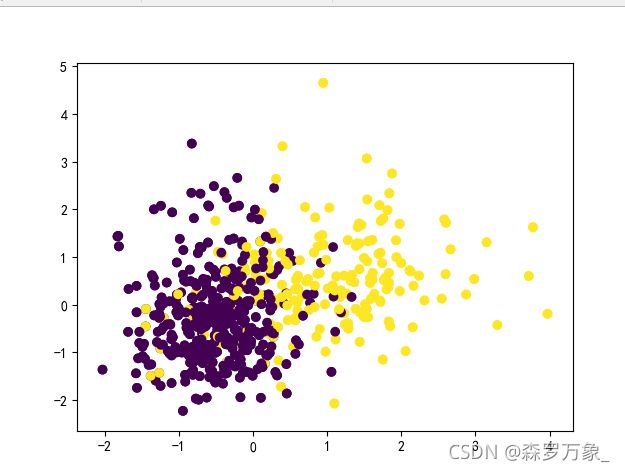
>>> #绘制原本的类别
... plt.scatter(X[: , 0], X[: , 1], c = y) 
<matplotlib.collections.PathCollection object at 0x0000012C77074438>
>>> plt.rcParams['font.sans-serif'] = 'SimHei'
>>> plt.rcParams['axes.unicode_minus'] = False
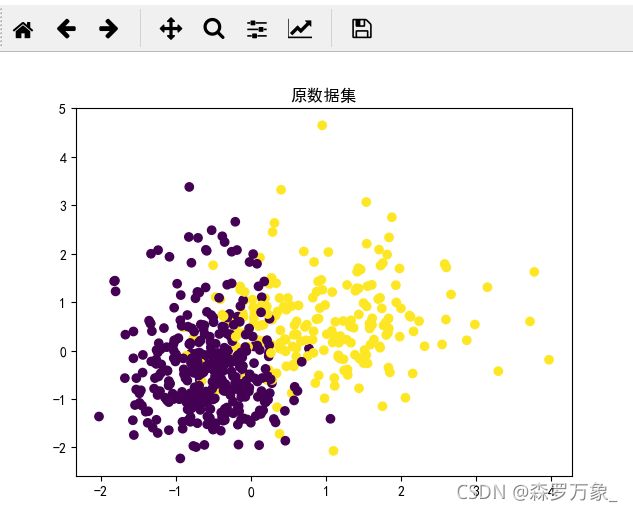
>>> plt.title('原数据集')
Text(0.5,1,'原数据集')
>>> plt.show()

>>> class LVQ():
...     def __init__(self, max_iter=10000, eta=0.1, e=0.15):
...         self.max_iter = max_iter
...         self.eta = eta
...         self.e = e
...     # 计算欧式距离
...     def dist(self, x1, x2):
...         return np.linalg.norm(x1 - x2)
...     # 产生原型向量
...     def get_vector(self, X, Y):
...         k = len(set(Y))
...         index = np.random.choice(X.shape[0], 1, replace=False)
...         mus = []
...         mus.append(X[index])
...         mus_label = []
...         mus_label.append(Y[index])
...         for _ in range(k - 1):
...             max_dist_index = 0
...             max_distance = 0
...             for j in range(X.shape[0]):
...                 min_dist_with_mu = 999999
... 
...                 for mu in mus:
...                     dist_with_mu = self.dist(mu, X[j])
...                     if min_dist_with_mu > dist_with_mu:
...                         min_dist_with_mu = dist_with_mu
... 
...                 if max_distance < min_dist_with_mu:
...                     max_distance = min_dist_with_mu
...                     max_dist_index = j
...             mus.append(X[max_dist_index])
...             mus_label.append(Y[max_dist_index])
... 
...         vector_array = np.array([])
...         for i in range(k):
...             if i == 0:
...                 vector_array = mus[i]
...             else:
...                 mus[i] = mus[i].reshape(mus[0].shape)
...                 vector_array = np.append(vector_array, mus[i], axis=0)
...         vector_label_array = np.array(mus_label)
...         return vector_array, vector_label_array
... 
...     def get_vector_index(self, x):
...         min_dist_with_mu = 999999
...         index = -1
... 
...         for i in range(self.vector_array.shape[0]):
...             dist_with_mu = self.dist(self.vector_array[i], x)
...             if min_dist_with_mu > dist_with_mu:
...                 min_dist_with_mu = dist_with_mu
...                 index = i
... 
...         return index
... 
...     def fit(self, X, Y):
...         self.vector_array, self.vector_label_array = self.get_vector(X, Y)
...         iter = 0
... 
...         while(iter < self.max_iter):
...             old_vector_array = copy.deepcopy(self.vector_array)
...             index = np.random.choice(Y.shape[0], 1, replace=False)
... 
...             vector_index = self.get_vector_index(X[index])
...             if self.vector_label_array[vector_index] == Y[index]:
...                 self.vector_array[vector_index] = self.vector_array[vector_index] + self.eta * (X[index] - self.vector_array[vector_index])
...             else:
...                 self.vector_array[vector_index] = self.vector_array[vector_index] - self.eta * (X[index] - self.vector_array[vector_index])
...             diff = 0
...             for i in range(self.vector_array.shape[0]):
...                 diff += np.linalg.norm(self.vector_array[i] - old_vector_array[i])
...             if diff < self.e:
...                 print('迭代{}次退出'.format(iter))
...                 return
...             iter += 1
...         print("迭代超过{}次，退出迭代".format(self.max_iter))
>>> lvq=LVQ()
>>> lvq.fit(X,y)
迭代599次退出
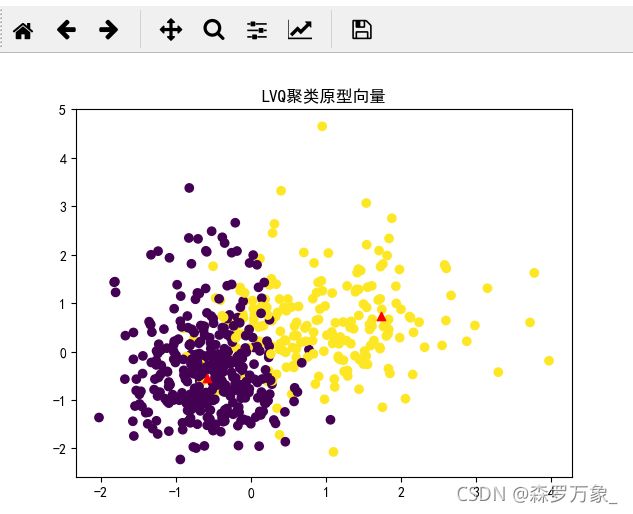
vector = lvq.vector_array
# 绘制获取的原型向量
fig = plt.figure(1)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.scatter(vector[:, 0], vector[:, 1], marker='^', c='r')
plt.title('LVQ聚类原型向量')
plt.show()

3.3.3.高斯混合聚类

高斯混合聚类算法是通过高斯混合分布的概率模型,给出聚类结果的一种原型聚类算法.

使用sklearn库的GaussianMixture类构建GMM聚类模型

>>> data=pd.read_csv('C:\\Users\\PC\\Desktop\\data\\data\\data.csv')
>>> x=data.iloc[:,2:]
>>> y=data.iloc[:,1]
>>> scaler=StandardScaler()
>>> scaler.fit(x)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> x=scaler.transform(x)
>>> plt.rcParams['font.sans-serif'] = 'SimHei'
>>> plt.rcParams['axes.unicode_minus'] = False
>>> plt.title('原始',size=17)
Text(0.5,1,'原始')
>>> plt.scatter(X[: , 0], X[: , 1], c = y)
<matplotlib.collections.PathCollection object at 0x000001D16B79D2B0>
>>> plt.show()

>>> gmm=GaussianMixture(n_components=2).fit(x)
>>> gmm_pre=gmm.predict(x)
>>> plt.scatter(x[:,0],x[:,1],c=gmm_pre)
<matplotlib.collections.PathCollection object at 0x000001D16BD4A518>
>>> plt.title('GMM',size=17)
Text(0.5,1,'GMM')
>>> plt.show()

3.4.密度聚类

基于密度的聚类算法简称密度聚类算法,该类算法假设聚类结果能够通过样本分布的紧密程度确定.其基本思想是,以样本在空间分布上的稠密程度为依据进行聚类.若区域中的样本密度大于某个阈值,则把相应的样本点划入与之相近的簇中.具有噪声的基于密度聚类(DBSCAN)是一种典型的密度聚类算法.该算法从样本密度的角度考察样本之间的可联接性,并由可连接样本不断扩展直到获得最终的聚类结果

>>> data = pd.read_csv('C:\\Users\\PC\\Desktop\\data\\data\\data.csv')
>>> X=data.iloc[:,2:]
>>> y=data.iloc[:,1].values
>>> #数据标准化
... from sklearn.preprocessing import StandardScaler
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> #绘制原本的类别
... plt.scatter(X[: , 0], X[: , 1], marker = 'o')
<matplotlib.collections.PathCollection object at 0x000001D16BF04BA8>
>>> plt.show()

>>> from sklearn.cluster import DBSCAN
>>> dbs = DBSCAN(eps =3, min_samples = 4).fit(X)
>>> print('DBSCAN模型:\n', dbs)
DBSCAN模型:
 DBSCAN(algorithm='auto', eps=3, leaf_size=30, metric='euclidean',
    metric_params=None, min_samples=4, n_jobs=1, p=None)
>>> # 绘制DBSCAN模型聚类结果
... ds_pre = dbs.fit_predict(X)
... 
>>> plt.scatter(X[: , 0], X[: , 1], c = ds_pre)
<matplotlib.collections.PathCollection object at 0x000001D16BD5DF98>
>>> plt.title('DBSCAN', size = 17)
Text(0.5,1,'DBSCAN')
>>> plt.show()

3.5.层次聚类

层次聚类又称为系统聚类,它试图在不同层次上对样本集进行划分,从而形成树形的聚类结构.样本集的划分可采用聚集系统法,也可采用分给系统法

聚集系统法是一种"自底向上"的聚合策略.它的基本思想是,开始时将每个样本作为单独的一类,然后将距离最近的两类合并成一个新类,重复进行将最近的两类合并成一类,直至所有的样本归为一类

分割系统法与聚集系统法想法,它是一种"自顶向下"的分割策略.它的基本思想是,开始时将整个样本集作为一类,然后按照将某种最优准则将它分割成距离尽可能远的两个子类,再用同样的方法将每个子类分割成两个子类,从中选择一个最优的子类,则此时样本集被划分出三类.一次类推,直至每个样本自成一类或达到设置的终止条件

>>> #导入数据
... data = pd.read_csv('C:\\Users\\PC\\Desktop\\data\\data\\data.csv')
>>> X=data.iloc[:,2:]
>>> y=data.iloc[:,1].values
>>> #数据标准化
... from sklearn.preprocessing import StandardScaler
>>> scaler=StandardScaler()
>>> scaler.fit(X)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> X=scaler.transform(X)
>>> # 单链接层次聚类
... from sklearn.cluster import AgglomerativeClustering
>>> clusing_ward = AgglomerativeClustering(n_clusters = 2).fit(X)
>>> clusing_ward
AgglomerativeClustering(affinity='euclidean', compute_full_tree='auto',
            connectivity=None, linkage='ward', memory=None, n_clusters=2,
            pooling_func=<function mean at 0x000001D14E813730>)
>>> # 绘制单链接聚类结果
... cw_ypre = AgglomerativeClustering(n_clusters = 2).fit_predict(X)
>>> plt.scatter(X[: , 0], X[: , 1], c = cw_ypre)
<matplotlib.collections.PathCollection object at 0x000001D16C24E630>
>>> plt.rcParams['font.sans-serif'] = 'SimHei'
>>> plt.rcParams['axes.unicode_minus'] = False
>>> plt.title('单链接聚类', size = 17)
Text(0.5,1,'单链接聚类')
>>> plt.show()

4.异常检测

吴恩达课程学习补充p90-p95

对每个特征计算出正态分布的参数，给定一个新样本，将新样本的每个特征的概率累乘并与 $\varepsilon$ 比较，如果概率累乘很大，判断为正常
只用正常的数据拟合模型，在交叉验证集和测试集正常和异常的数据都存在，选用使得 F₁ 最小的 $\varepsilon$
有很少的异常样本，很多的正常样本，适用于异常检测，因为拟合数据只需要正常样本；异常样本和正常样本都有很多用监督学习
当某个特征的数据分布不符合正态分布时，可以进行一些处理，如用 $l o g (x)$ 取代 $x$
为了选择合适的特征，可以先训练模型，然后观察那些分类错误的样本，看看它们和正常样本的区别在哪里，从而选择新的特征
多元高斯分布直接计算某个样本的所有特征的概率，而不是计算每个特征的概率然后相乘。
用训练数据集拟合高斯分布中的参数 $\mu=\frac{1}{m}\sum_{i=1}^mx^{(i)}$ ， $\varSigma=\frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu)(x^{(i)}-\mu)^T$ 。 $\mu$ 是向量， $\varSigma$ 是协方差矩阵
得到新的样本后计算概率，如果小于某个值，就判断为异常
多元高斯分布模型要求样本数量远大于特征数量时才能表现很好

五、投入应用

在实际应用机器学习时，先利用较少的时间实现一个算法，并将收集到的数据应用其中，然后通过交叉验证或其他方法确定算法在随着样本数量增大时会获得更好的性能时再返回进一步收集数据，即只有确定需要大量数据之后，才去花费时间获取数据
在开发大型机器学习应用时，将整个工作流程分为几块，如数据----->模块1----->模块2----->模块3----->模块4，先利用少量数据完成整个流程，计算整个系统的准确率，然后手动处理代替模块1的内容，使数据完全正确地流入模块2，再次计算整个系统的准确率，然后手动处理代替模块2，使数据再次正确进入模块3，计算整个系统准确率，依次计算，完成一次遍历之后，就能够发现优化每个模块的收益上限。例如在实际处理中得到下面的数据

手动代替成分	整个系统准确度
模块1	0.72
模块1+模块2	0.89
模块1+模块2+模块3	0.90
模块1+模块2+模块3+模块4	1.00

那么花费时间优化模块1，得到的收益上限是0.17，同理能够计算出其他优化上限

六、应用案例

1.医疗保险的欺诈发现

随着我国医疗保险事业的快速发展,在保险赔付过程中,存在一些借助病例进行医疗保险欺诈的案件.医疗保险欺诈是指公民,法人或者其他组织在参加医疗保险,缴纳医疗保险费,享受医疗保险待遇过程中,故意捏造事实,弄虚作假,隐瞒真实情况等造成医疗保险基金损失的行为.骗保人进行医疗保险欺诈时通常使用的手段,一种是使用别人的医疗保险卡配药,另一种是在不同的医院和医生处重复配药.例如,单张处方药费特别高,同一张医疗保险卡在一定时间内反复多次配药等都有可能是医疗保险欺诈.

此案例收集了医疗保险投保人,医疗机构,索赔等相关历史数据,基于K-Means聚类算法对医疗保险投保人,医疗机构进行聚类分析,从而发现疑似医疗保险的欺诈行为

1.1.目标分析

近年来有关医疗保险欺诈的事件层出不穷,不法分子利用医疗保险赔偿,通过不同方式的医疗保险欺诈来谋取利益.医疗保险欺诈涉及三个角色.角色1是投保人,投保人作为医疗保险的受益者,投保人购买保险后,根据保险条款,当本人去看病时保险公司会承担一定比例的费用,并且这些费用不需要亲自找保险公司索取,而是在交费时自动扣除.角色2是医疗机构,医疗机构帮助投保人治疗疾病或者提供保健,并在投保人购买了保险时,会由医疗机构先垫付保险所覆盖的医疗保健费用,随后医疗机构会向保险公司索赔以配成这部分医疗费用.角色3是保险公司,保险公司通过向投保人提供医疗保险获得保费收入,再经过受理医疗机构的保险索赔进行支出,二者之间的差额就是它的经济来源.医疗保险欺诈具有强烈的行业特色,根据不同行业的业务发展特点,医疗保险欺诈由不同的欺诈模式.医疗保险欺诈索赔额过高时,将导致保险公司的利润下降甚至亏损,作为医疗保险赔偿方,保险公司会因此面临巨大风险.医疗保险的欺诈模式并非一成不变,通过不同的数据分析方法,对应不同的医疗保险欺诈行为模式,结合医疗保险行业特点,不断挖掘发现新的医疗保险欺诈模式,继而更新医疗保险欺诈模式库,完善医疗保险欺诈模型.

1.1.1.数据说明

列名	含义
Policy_HolderID	投保人编号
ProgramCode	保险条款
MEDcode	治疗措施编码
Age	年龄
Sex	性别

列名	含义
ProviderID	医疗机构编号
ProviderType	医疗机构大类
ProviderSpecialty	医疗机构细类
Location	位置编码

1.1.2.分析目标

医疗保险的欺诈发现包括以下流程

1.抽取医疗保险的历史数据

2.对抽取的医疗保险的历史数据进行描述性的统计分析,分析投保人的信息和医疗机构的信息

3.采用K-Means聚类算法发现投保人和医疗机构中存在的疑似欺诈行为

4.对疑似欺诈行为结构和聚类算法进行性能度量分析,并进行模型优化

1.2.数据准备

医疗保险数据可能无法直接用于建模,其中可能存在缺失值,特征类型不统一等问题,需要进行必要的数据准备

1.2.1.描述性统计分析

>>> import numpy as np
>>> import pandas as pd
>>> import matplotlib.pyplot as plt
>>> policy_holder=pd.read_csv('C:\\Users\\PC\\Desktop\\seven\\data\\Policy_Holder.csv',encoding='gbk')
>>> provider=pd.read_csv('C:\\Users\\PC\\Desktop\\seven\\data\\Provider.csv',encoding='gbk')
>>> claim=pd.read_csv('C:\\Users\\PC\\Desktop\\seven\\data\\Claim.csv',encoding='gbk')
#描述性统计分析,返回缺失值的个数以及特征的最大值,最小值
>>> explore_policy_holder=policy_holder.describe(percentiles=[],include='all').T
>>> explore_provider=provider.describe(percentiles=[],include='all').T
>>> explore_claim=claim.describe(percentiles=[],include='all').T
>>> explore_policy_holder['null']=policy_holder.isnull().sum()
>>> explore_policy_holder
                count unique              top ...     50%       max null
Policy_HolderID   400    NaN              NaN ...   4e+10  6.94e+10    0
ProgramCode       400      2            老年保障险 ...     NaN       NaN    0
MEDcode           400      5  RegularMedicare ...     NaN       NaN    0
Age               400    NaN              NaN ...      50        97    0
Sex               400      2                女 ...     NaN       NaN    0

[5 rows x 10 columns]
>>> explore_provider['null']=provider.isnull().sum()
>>> explore_provider
                  count unique        top ...           50%          max null
ProviderID          500    NaN        NaN ...   1.00476e+10  1.00862e+10    0
ProviderType        500     28  physician ...           NaN          NaN    0
ProviderSpecialty   500     39     clinic ...           NaN          NaN    0
Location            500    NaN        NaN ...           367          945    0

[4 rows x 10 columns]
>>> explore_claim['null']=claim.isnull().sum()
>>> explore_claim
         count unique             top ...           50%          max null
索赔编号      9462    NaN             NaN ...   4.04745e+14   9.9796e+14    0
医疗机构编号    9462    NaN             NaN ...   1.00424e+10  1.00862e+10    0
投保人编号     9462    NaN             NaN ...      3.98e+10     6.93e+10    0
投保人状态     9462      6    StillPatient ...           NaN          NaN    0
医疗机构服务类别  9462     10  PhysicianOther ...           NaN          NaN    0
诊断        9462    124           V41.1 ...           NaN          NaN    0
处理过程代码    9462    NaN             NaN ...            29           90    0
住院时长      9462    NaN             NaN ...            18           67    0
住院开始时间    9462    365      2001-01-01 ...           NaN          NaN    0
住院结束时间    9462    412      2001-09-13 ...           NaN          NaN    0
保费覆盖额     9462    NaN             NaN ...         31300        99900    0
账单金额      9462    NaN             NaN ...         31888        99940    0
支付金额      9462    NaN             NaN ...       30868.5        99676    0
服务地点      9462      8       residence ...           NaN          NaN    0

从输出可以看出,各表的特征中不存在缺失值;由于大部分特征为字符型,不存在特征的最大值和最小值

1.2.2.数据清洗

数据清洗的主要内容为格式与内容不规范的数据.主要包括:

1.在三张数据表中,投保人编号,医疗机构编号和索赔编号数据类型不统一,将三者统一为字符型,便于后续的特征提取

2.将投保人信息表,医疗机构信息表中的变量进行更改

3.将索赔信息表中的住院开始时间,住院结束时间的数据类型统一为时间类型

#统一数据类型
>>> policy_holder[['Policy_HolderID']]=policy_holder[['Policy_HolderID']].astype(str)
>>> provider[['ProviderID']]=provider[['ProviderID']].astype(str)
>>> claim[['索赔编号']]=claim[['索赔编号']].astype(str)
>>> claim[['医疗机构编号']]=claim[['医疗机构编号']].astype(str)
>>> claim[['投保人编号']]=claim[['投保人编号']].astype(str)
#更改表的变量
>>> policy_holder.columns=['投保人编号','保险条款','治疗措施编码','年龄','性别']
>>> provider.columns=['医疗机构编号','医疗机构大类','医疗机构小类','位置编码']
#转变时间数据类型
>>> claim['住院开始时间']=pd.to_datetime(claim['住院开始时间'],format="%Y-%m-%d")
>>> claim['住院结束时间']=pd.to_datetime(claim['住院结束时间'],format="%Y-%m-%d")

#### 1.2.3.信息分析

分析保险条款种类

```python
>>> ProgramCode=pd.value_counts(policy_holder['保险条款'])
>>> plt.pie(ProgramCode,labels=ProgramCode.index,autopct='%1.2f%%')
([<matplotlib.patches.Wedge object at 0x000001CEDFFF0438>, <matplotlib.patches.Wedge object at 0x000001CEDFFF0BA8>], [Text(-0.00863928,1.09997,'老年保障险'), Text(0.00863928,-1.09997,'伤残险')], [Text(-0.00471234,0.599981,'50.25%'), Text(0.00471234,-0.599981,'49.75%')])
>>> plt.rcParams['font.sans-serif'] = ['SimHei']
>>> plt.rcParams['axes.unicode_minus'] = False
>>> plt.title('保险条款种类的比率饼图')
Text(0.5,1,'保险条款种类的比率饼图')
>>> plt.legend()
<matplotlib.legend.Legend object at 0x000001CEDFFD3E48>
>>> plt.show()

分析治疗措施编码类型

>>> MEDCode=pd.value_counts(policy_holder['治疗措施编码'])
>>> plt.figure(figsize=(8,5))
<Figure size 800x500 with 0 Axes>
>>> plt.bar(MEDCode.index,MEDCode,width=0.4,color='skyblue')
<BarContainer object of 5 artists>
>>> plt.xlabel('治疗措施编码')
Text(0.5,0,'治疗措施编码')
>>> plt.ylabel('频数')
Text(0,0.5,'频数')
>>> plt.title('治疗措施编码种类的条形图')
Text(0.5,1,'治疗措施编码种类的条形图')
>>> plt.show()

分析投保人所投保险的年龄分布

>>> old_distribute=policy_holder.loc[policy_holder['保险条款']=='老年保障险',:]
>>> old_distribute_age=pd.value_counts(old_distribute['年龄'])
>>> plt.figure(figsize=(12,8))
<Figure size 1200x800 with 0 Axes>
>>> plt.subplot(121)
<matplotlib.axes._subplots.AxesSubplot object at 0x000001CEDFAE56A0>
>>> plt.bar(old_distribute_age.index,old_distribute_age)
<BarContainer object of 74 artists>
>>> plt.title('老年保障险分布情况')
Text(0.5,1,'老年保障险分布情况')
>>> plt.xlabel('年龄')
Text(0.5,0,'年龄')
>>> plt.ylabel('频数')
Text(0,0.5,'频数')
>>> insurance_disability=policy_holder.loc[policy_holder['保险条款']=='伤残险',:]
>>> insurance_disability_age=pd.value_counts(insurance_disability['年龄'])
>>> plt.subplot(122)
<matplotlib.axes._subplots.AxesSubplot object at 0x000001CEE080DE80>
>>> plt.bar(insurance_disability_age.index,insurance_disability_age)
<BarContainer object of 71 artists>
>>> plt.title('伤残险分布情况')
Text(0.5,1,'伤残险分布情况')
>>> plt.xlabel('年龄')
Text(0.5,0,'年龄')
>>> plt.ylabel('频数')
Text(0,0.5,'频数')
>>> plt.show()

在这里插入图片描述

从图中可以看出,在老年保障险和伤残险的投保人中,年龄分布有较大差异.其中伤残险的投保人一般无年龄特别小的投保人,不小于16岁;而老年保障险的投保人则出现比较小的情况.这个现象说明,意外事故等伤残情况容易发生在少年阶段及以上的人群;而老年保障险有年龄小的投保人,表明该保险较受有孩子家庭的欢迎

分析医疗机构信息

>>> provider_type=pd.value_counts(provider['医疗机构大类'])
>>> plt.figure(figsize=(10,6))
<Figure size 1000x600 with 0 Axes>
>>> plt.bar(provider_type.index,provider_type)
<BarContainer object of 28 artists>
>>> plt.xticks(rotation=90)
([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27], <a list of 28 Text xticklabel objects>)
>>> plt.title('医疗机构大类分布图')
Text(0.5,1,'医疗机构大类分布图')
>>> plt.xlabel('医疗机构大类')
Text(0.5,0,'医疗机构大类')
>>> plt.ylabel('频数')
Text(0,0.5,'频数')
>>> plt.tight_layout() #加上可以合理安排布局
>>> plt.show()

从图中可以看出,physician(内科)所占的份额最多,相比之下,其他类别只占少数.此结果在一定程度上反映出在日常生活中,人们关注的疾病问题多数与内科有关.内科包含范围广,能够在多方面引起身体不适,因此人们应更注意这方面的健康问题

1.3.特征工程

此案例的特征工程是对不同主体对象构建特征,通过分别对投保人,医疗机构的出险和索赔模式前后发生变化判断疑似医疗保险的欺诈行为

根据医疗保险行业的业务知识,投保人作为用户对象,出险模式和索赔模式应具有一致性,即在一段时间内不应该有发生较大的变化.为了体现出出险模式和索赔模式的变化,可根据投保人的住院开始时间属性将其划分为上半年和下半年两个部分.该模型使用K-Means聚类的方法,将在上半年与下半年出险模式和索赔模式发生较大变化的投保人视为疑似医疗保险的欺诈行为

发现医疗机构行为模式异常模型的构建与发现投保人疑似欺诈模型的思路类似,区别在于模型对象不同,发现投保人疑似欺诈模型的分析对象为投保人,发现医疗机构行为模式异常模型的对象针对的是医疗机构.同样地,医疗机构的索赔模式在一段时间内也应该具有一致性,可将索赔模式前后发生变化的医疗机构判断存在疑似医疗保险的欺诈行为

1.3.1.特征选择

根据提取的特征结果,通过K-Means聚类算法对投保人划分人群.再根据投保人的类群分布统计平均半年支付金额,平均半年支付笔数和投保人数量,分析各类群之间相关特征差异.然后统计投保人类群的迁移情况,即上半年与下半年出险和索赔类群发生变化的情况,将投保人类群迁移变化较大的投保人视为存在疑似医疗保险的欺诈行为

投保人特征选择

说明	特征
投保人信息表	投保人编号,年龄,性别,治疗措施编码,保险条款
索赔信息表	医疗机构编号,投保人编号,住院开始时间,保险费覆盖额,账单金额,支付金额

医疗机构特征选择

说明	特征
医疗机构信息表	医疗机构编号,医疗机构大类,医疗机构细类
索赔信息表	医疗机构编号,住院开始时间,保险费覆盖额,账单金额,支付金额,处理过程代码

1.3.2.特征变换

部分投保人并非在某段固定时间内发生索赔,索赔和不索赔的状态变化也是重要的特征.因此在需要考虑出险和索赔过程的时间,此案例将投保人的住院开始使劲按划分为上半年和下半年,再对不同对象特征进行特征变换

1.3.2.1.投保人特征变换

对投保人提取特征并进行特征变换,具体的特征变换内容包括:

1.根据投保人的住院开始时间将其划分为上半年(1H)和下半年(2H)两部分

2.根据索赔订单中的保费覆盖额,账单金额,支付金额特征,分别按上半年和下半年进行统计,分别得到半年保费覆盖额,半年账单金额,半年支付金额和半年支付笔数

3.选取投保人信息表中的年龄(Age),性别(Sex,取值范围为女和男),治疗措施编码(MEDcode,取值范围为MCbuy,RegularMedicare,MCD,MCQ,Undocumented),保险条款属性(ProgramCode,取值范围为伤残险和老年保障险)特征,除年林之外的特征采用虚构变量法,即按值展开

>>> claim_money = claim.loc[:, ['医疗机构编号', '投保人编号', '住院开始时间','保费覆盖额', '账单金额', '支付金额']]
>>> claim_money['住院开始时间'] = claim_money['住院开始时间'].dt.month.astype(int)
#按照住院时间划分为上半年和下半年
>>> claim_money['所属时间段']=0
>>> claim_money.loc[claim_money['住院开始时间']<=6,'所属时间段']='1H'
>>> claim_money.loc[claim_money['住院开始时间']>6,'所属时间段']='2H'
#根据投保人编号统计上半年和下半年的索赔支付笔数总数
>>> claim_paycount=claim_money.groupby(['投保人编号','所属时间段'])['医疗机构编号'].count()
>>> claim_paycount=claim_paycount.reset_index()
>>> claim_paycount.columns=['投保人编号','所属时间段','半年支付笔数']
#根据投保人编号统计上半年和下半年保费覆盖额,账单金额,支付金额总额
>>> claim_moneysum=claim_money.groupby(['投保人编号','所属时间段'])['保费覆盖额','账单金额','支付金额'].sum()
>>> claim_moneysum=claim_moneysum.reset_index()
>>> claim_moneysum.columns=['投保人编号','所属时间段','半年保费覆盖额','半年账单金额','半年支付金额']
>>> claim_part=pd.merge(claim_moneysum,claim_paycount,on=['投保人编号','所属时间段'])
>>> policy_holder_t=policy_holder
>>> policy_holder_t=pd.concat([policy_holder_t,policy_holder],axis=0)
>>> policy_holder_t['所属时间段']=0
>>> policy_holder_t.index=range(len(policy_holder_t))
#确保每个投保人有两条记录
>>> policy_holder_t.loc[0:400,'所属时间段']='1H'
>>> policy_holder_t.loc[400:800,'所属时间段']='2H'
>>> claim_policy=pd.merge(claim_part,policy_holder_t,how='outer')
>>> claim_policy=claim_policy.fillna(0)
>>> model3_data1=pd.concat([claim_policy.loc[:,['半年保费覆盖额','半年账单金额','半年支付金额','半年支付笔数','年龄']],pd.get_dummies(claim_policy['性别']),pd.get_dummies(claim_policy['治疗措施编码']),pd.get_dummies(claim_policy['保险条款'])],axis=1)
>>> model3_data=model3_data1.copy()

1.3.2.2.医疗机构特征变换

医疗机构特征变换过程与投保人特征变换过程类似,具体特征变换过程包括

1.先根据索赔信息表中投保人的住院开始时间将其划分为上半年(1H)和下半年(2H)两部分

2.按医疗机构编号和所属时间段进行分组,统计投保人数和处理过程量;选取索赔订单中保费覆盖额,账单金额和支付金额的特征,分别按上半年和下半年进行统计,分别得到半年保费覆盖额,半年账单金额,半年支付金额,半年支付笔数.再选取医疗机构信息表中医疗机构大类(ProviderType),医疗机构细类(ProviderSpecialty)和位置编码(Location)三个特征

3.由于医疗机构大类和医疗机构细类取值都为字符串类型,需要把字符串类型转为数值型,使用sklearn.preprocessing库中的LabelEncoder函数将非数值型标签值标准化

>>> from sklearn.preprocessing import LabelEncoder
>>> provider_t=provider.copy()
>>> provider_t=pd.concat([provider_t,provider],axis=0)
>>> provider_t['所属时间段']=0
>>> provider_t.index=range(len(provider_t))
#确保每个医疗机构都有两条记录
>>> provider_t.loc[:500,'所属时间段']='1H'
>>> provider_t.loc[500:1000,'所属时间段']='2H'
#统计数据
>>> money_sum=claim_money.groupby(['医疗机构编号','所属时间段'])['保费覆盖额','账单金额','支付金额'].sum()
>>> money_sum=money_sum.reset_index()
>>> money_sum.columns=['医疗机构编号','所属时间段','半年保费覆盖额','半年账单金额','半年支付金额']
#汇总
>>> claim_money['处理过程代码']=claim['处理过程代码']
>>> claim_money['处理过程代码']=claim_money['处理过程代码'].astype(str)
>>> count1=claim_money.groupby(['医疗机构编号','所属时间段'])['处理过程代码'].count()
>>> deal_count=count1.reset_index()
>>> deal_count.columns=['医疗机构编号','所属时间段','处理过程数量']
#合并并标准化数据
>>> claim_money['投保人编号']=claim_money['投保人编号'].astype(str)
>>> count2=claim_money.groupby(['医疗机构编号','所属时间段'])['投保人编号'].count()
>>> people_count=count2.reset_index()
>>> people_count.columns=['医疗机构编号','所属时间段','投保人数量']
>>> people_deal=pd.merge(people_count,deal_count,on=['医疗机构编号','所属时间段'])
>>> pd_money=pd.merge(people_deal,money_sum,on=['医疗机构编号','所属时间段'])
>>> claim_provider=pd.merge(pd_money,provider_t,how='outer')
>>> claim_provider=claim_provider.fillna(0)
>>> claim_provider_original=claim_provider.copy()
>>> class_le=LabelEncoder()
>>> claim_provider['医疗机构大类']=class_le.fit_transform(claim_provider['医疗机构大类'].values)+1
>>> claim_provider['医疗机构细类']=class_le.fit_transform(claim_provider['医疗机构细类'].values)+1

1.4.模型训练

原始数据集中不存在真实标签,所以采用机器学习中的无监督学习算法构建医疗保险的欺诈模型,此案例采用K-Means聚类算法分别对经过特征变换后投保人和医疗机构的特征集进行分群

发现投保人疑似医疗保险的欺诈模型训练

>>> from sklearn.cluster import KMeans
>>> from sklearn.preprocessing import StandardScaler
>>> scaler=StandardScaler()
>>> scaler.fit(model3_data1)
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> model3_data=scaler.transform(model3_data1)
>>> kmeans=KMeans(n_clusters=5,random_state=0)
>>> kmeans.fit(model3_data)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
    n_clusters=5, n_init=10, n_jobs=1, precompute_distances='auto',
    random_state=0, tol=0.0001, verbose=0)
>>> label_pred=kmeans.labels_
>>> model3_centers1=kmeans.cluster_centers_
>>> model3_centers=model3_centers1.copy()
>>> model3_centers
array([[-0.33816459, -0.33812701, -0.33816837, -0.33657325,  0.06039226,
         0.08099355, -0.08099355, -0.18328047, -0.31448545, -0.26904657,
         0.50390326, -0.11250879,  1.00501256, -1.00501256],
       [ 2.27902466,  2.27909801,  2.27876965,  2.27978935, -0.15022653,
         0.09354188, -0.09354188,  0.0958977 ,  0.16987058, -0.22958246,
         0.01114857, -0.11250879,  0.01490118, -0.01490118],
       [-0.36025685, -0.36026183, -0.36024162, -0.35697585, -0.07400963,
        -0.08820468,  0.08820468, -0.18328047, -0.31448545, -0.26904657,
         0.50390326, -0.11250879, -0.99501244,  0.99501244],
       [-0.3847462 , -0.38478986, -0.3845017 , -0.38793386, -0.00918135,
        -0.22810714,  0.22810714, -0.18328047, -0.31448545,  3.7168286 ,
        -1.9845079 , -0.11250879,  0.09934086, -0.09934086],
       [-0.1718047 , -0.17196418, -0.17169663, -0.18601131,  0.21780593,
         0.05129943, -0.05129943,  1.14736427,  1.9626876 , -0.26904657,
        -1.9845079 ,  0.89880618, -0.11859699,  0.11859699]])
>>> for i in range(model3_centers1.shape[1]):
...     model3_centers[:,i] = model3_centers1[:,i]*(max(model3_data1.iloc[:,i])-min(model3_data1.iloc[:,i])) + min(model3_data1.iloc[:,i])
>>> claim_policy['cluster']=label_pred
>>> claim_policy
           投保人编号 所属时间段    半年保费覆盖额   ...     年龄  性别  cluster
0    10300010118    1H  1240200.0   ...     27   男        0
1    10300010118    2H  1051400.0   ...     27   男        0
2    10500010200    1H   247800.0   ...     49   男        0
3    10600010291    2H   785400.0   ...     28   男        0
4    10700010301    2H    43800.0   ...     92   女        0
.
21   12800011526    1H   128000.0   ...     35   女        2
...
>>> data=claim_policy.loc[:,['投保人编号','所属时间段','cluster']]
>>> id=np.unique(data.loc[:,'投保人编号'])
>>> df=pd.DataFrame(columns=['投保人编号','所属时间段','类群'])
for i in range(400):
...     line1=data[data['投保人编号']==id[i]].iloc[0,:]
...     line2=data[data['投保人编号']==id[i]].iloc[1,:]
...     if line1['cluster']!=line2['cluster']:
...         df=df.append(line1)
...         df=df.append(line2)
>>> result=np.unique(df.loc[:,'投保人编号'])
>>> result
array(['11700010743', '16500013059', '18700014183', '24900016750',
       '26600017742', '28900018722', '29600018811', '31200019485',
       '32100019963', '35600021591', '38400023092', '39200023361',
       '39300023401', '40400023860', '44600026120', '46300027224',
       '50900029514', '53300030765', '53700030960', '58200033387',
       '60000033912', '61200034537', '64500036177', '65200036567',
       '65500036707', '67000037367', '67400037634', '68000037855',
       '68500038167'], dtype=object)

得到的 result 投保人编号所对应的投保人存在出险和索赔模式前后变化不一致的情况,可以初步推测这些投保人存在医疗保险欺诈行为

发现医疗机构疑似医疗保险欺诈模型训练

scaler = StandardScaler()
scaler.fit(claim_provider.iloc[:,2:10])
claim_provider.iloc[:,2:10] = scaler.transform(claim_provider.iloc[:,2:10])
model4_km  = KMeans(n_clusters = 5,random_state = 0)  # K-Means聚类
model4_km .fit(claim_provider.iloc[:,2:10])  # 预测
model4_label_pred = model4_km .labels_
model4_centers1 = model4_km .cluster_centers_

采取同样的方法可以获得疑似医疗保险诈骗的医疗机构编号

1.5.性能度量

对于模型的性能度量,可以对模型的结果进行分析和对K-Means聚类算法的聚类性能进行度量.其中聚类性能的度量方法有ARI评价法(兰德系数),AMI评价法(互信息),V-measure评分,FMI评价法,轮廓系数评价法和Calinski-Harabasz指标评价法等.由于前四种方法需要真实值的配合才能够评价聚类算法的优劣,后两种方法则不需要真实值的配合.由于原始数据本身并不存在真实分类结果,此案例采用轮廓系数评价法和Calinski-Harabasz指标评价法进行聚类性能度量

1.5.1.结果发现

发现投保人的医疗保险欺诈结果分析

为了发现投保人的医疗保险欺诈行为,将投保人聚类成五类类群,选取投保人数量,平均支付金额,平均支付笔数等具有代表性的指标,进行聚类群之间的差异比较

claim_cluster = claim_policy.groupby('cluster')['半年支付金额','半年支付笔数'].mean()
claim_cluster = claim_cluster.reset_index()
claim_cluster.columns = ['类群编号','支付金额_mean','支付笔数_mean']
claim_cluster['投保人数量'] = pd.value_counts(claim_policy['cluster'])
model3_result1 = claim_policy.loc[claim_policy['所属时间段'] == "1H", :]
model3_result2 = claim_policy.loc[claim_policy['所属时间段'] == "2H", :]
model3_result2.columns = ['投保人编号', '所属时间段_2','保费覆盖额_halfyear_2','账单金额_halfyear_2', '支付金额_halfyear_2','支付笔数_halfyear_2', '保险条款_2', '治疗措施编码_2', '年龄_2', '性别_2', 'cluster_2']
model3_result = pd.merge(model3_result1, model3_result2, on=['投保人编号'])  # 合并
model3_migrate = pd.crosstab(model3_result ['cluster'], model3_result['cluster_2'])
model3_ysqz = model3_result.loc[model3_result.loc[:, 'cluster'] !=model3_result.loc[:, 'cluster_2'],:]
model3_ysqz = model3_ysqz.loc[:,['投保人编号', 'cluster', 'cluster_2']]
model3_ysqz.to_csv('../tmp/policy_holder_ysqz.csv', index=False)
>>> model3_migrate
cluster_2    0   1    2   3   4
cluster                        
0          133   3    0   0   0
1           10  36   10   0   5
2            0   0  134   0   0
3            0   1    0  26   0
4            0   0    0   0  42
>>> claim_cluster
   类群编号     支付金额_mean  支付笔数_mean  投保人数量
0     0  1.887588e+05   5.003584    279
1     1  2.211617e+06  58.049505    101
2     2  1.716965e+05   4.589928    278
3     3  1.529438e+05   3.962264     53
4     4  3.174392e+05   8.056180     89

类群0和2的投保人,相对应的品军支付金额与品骏支付笔数并不大,而类群1的投保人的品骏支付金额和平均支付笔数却明显大于其他类群,投保人数量却远少于其他类群,因此可以判定该类群的投保人可能存在医疗保险欺诈行为

发现医疗机构的医疗保险欺诈结果分析


claim_provider_original['类群编号'] = model4_label_pred
collect_compare = pd.value_counts(claim_provider_original['类群编号'])
collect_compare = collect_compare.reset_index()
collect_compare.columns = ['类群编号', '医疗机构数量']
collect_compare = collect_compare.sort_values(by='类群编号')
collect_compare.index = range(len(collect_compare))

# 根据投保人编号统计上下半年保费覆盖额,账单金额,支付金额总额
collect_compare['平均投保人数量']  = claim_provider_original.groupby(['类群编号'])['投保人数量'].mean()

# 计算不同类群间账单金额的平均值
collect_compare['平均账单金额'] = claim_provider_original.groupby(['类群编号'])['半年账单金额'].mean()
claim_provider_original['所属时间段'] = claim_provider_original['所属时间段']
model4_colunms = ['医疗机构编号', '投保人数量','处理过程数量','半年保费覆盖额','半年账单金额','半年支付金额', '类群编号']
# 划分上半年数据
model4_result1 = claim_provider_original.loc[claim_provider_original['所属时间段'] == '1H',: ]
model4_result1 = model4_result1.loc[:, model4_colunms] 
model4_result1.columns = ['医疗机构编号', '投保人数量1', '处理过程数量1','保费覆盖额1', '账单金额1', '支付金额1', '类群编号1']

# 划分下半年数据
model4_result2 = claim_provider_original.loc[claim_provider_original['所属时间段'] == '2H',: ]
model4_result2  = model4_result2.loc[:, model4_colunms]   
model4_result2.columns = ['医疗机构编号', '投保人数量2', '处理过程数量2','保费覆盖额2', '账单金额2', '支付金额2', '类群编号2']
model4_result = pd.merge(model4_result1,model4_result2,on=['医疗机构编号']) #合并上下半年的数据
model4_ysqz = model4_result.loc[model4_result.loc[:, '类群编号1'] != model4_result.loc[:, '类群编号2'],:]
model4_migrate = pd.crosstab(model4_result ['类群编号1'], model4_result ['类群编号2']) #查看类群迁移情况

# 根据类群的迁移变化选择出疑似欺诈的情况
model4_ysqz= model4_ysqz.loc[:,['医疗机构编号', '类群编号1', '类群编号2']]
model4_ysqz.to_csv('../tmp/Provider_ysqz.csv', index=False)

1.5.2.聚类性能度量

由于原始数据本身不存在真实分类结果,所以发现投保人疑似医疗保险欺诈行为和发现医疗疑似医疗欺诈行为都是基于K-Means聚类算法,分类效果度量采用轮廓系数评价法和Calinski-Harabasz指标评价法对聚类模型进行评价

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabaz_score
import matplotlib.pyplot as plt
silhouettteScore3 = []
calinskiharabazScore3 = []
for i in range(2, 12):
    kmeans_num31 = KMeans(n_clusters = i, random_state = 0).fit(model3_data)  # 构建并训练模型
    score = silhouette_score(model3_data, kmeans_num31.labels_)  # 轮廓系数
    silhouettteScore3.append(score)
    print('数据聚%d类silhouette_score指数为：%f'%(i,score))
    score1 = calinski_harabaz_score(model3_data, kmeans_num31.labels_)
    calinskiharabazScore3.append(score1)
    print('数据聚%d类calinski_harabaz指数为：%f'%(i, score1))

# 绘制折线图   
plt.figure(figsize=(8, 5))
plt.rcParams['font.sans-serif'] = 'SimHei'  # 显示中文
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(1, 2, 1)  # 子图
plt.plot(range(2, 12),silhouettteScore3, 'ko-', linewidth=1.5)
plt.title('轮廓系数评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.subplot(1,2,2)  
plt.plot(range(2, 12), calinskiharabazScore3, 'o-', linewidth=1.5)
plt.title('Calinski-Harabasz指标评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.savefig('../tmp/policy_holder_ysqz.jpg') 
plt.show()
plt.close


silhouettteScore4 = []  # 轮廓系数
calinskiharabazScore4 = []  # Calinski-Harabasz
for i in range(2, 12):
    kmeans_num41 = KMeans(n_clusters = i, random_state=0).fit(claim_provider.iloc[:, 2:10])  # 构建并训练模型
    score = silhouette_score(claim_provider.iloc[:, 2:10], kmeans_num41.labels_)
    silhouettteScore4.append(score)
    print('数据聚%d类silhouette_score指数为：%f'%(i,score))
    score1 = calinski_harabaz_score(claim_provider.iloc[:, 2:10],
                                    kmeans_num41.labels_)
    calinskiharabazScore4.append(score1)
    print('数据聚%d类calinski_harabaz指数为：%f'%(i,score1))

# 绘制折线图
plt.figure(figsize=(8, 5))
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(1,2,1)  # 子图
plt.plot(range(2,12),silhouettteScore4, 'ko-', linewidth=1.5)
plt.title('轮廓系数评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.subplot(1, 2, 2)  
plt.plot(range(2, 12), calinskiharabazScore4, 'o-', linewidth=1.5)
plt.title('Calinski-Harabasz指标评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.savefig('../tmp/Provider_ysqz_evaluate.jpg')
plt.show()
plt.close

model4_result = pd.merge(model4_result1,model4_result2,on=[‘医疗机构编号’]) #合并上下半年的数据
model4_ysqz = model4_result.loc[model4_result.loc[:, ‘类群编号1’] != model4_result.loc[:, ‘类群编号2’],:]
model4_migrate = pd.crosstab(model4_result [‘类群编号1’], model4_result [‘类群编号2’]) #查看类群迁移情况

根据类群的迁移变化选择出疑似欺诈的情况

model4_ysqz= model4_ysqz.loc[:,[‘医疗机构编号’, ‘类群编号1’, ‘类群编号2’]]
model4_ysqz.to_csv(’…/tmp/Provider_ysqz.csv’, index=False)


#### 1.5.2.聚类性能度量

由于原始数据本身不存在真实分类结果,所以发现投保人疑似医疗保险欺诈行为和发现医疗疑似医疗欺诈行为都是基于K-Means聚类算法,分类效果度量采用轮廓系数评价法和Calinski-Harabasz指标评价法对聚类模型进行评价

```python
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabaz_score
import matplotlib.pyplot as plt
silhouettteScore3 = []
calinskiharabazScore3 = []
for i in range(2, 12):
    kmeans_num31 = KMeans(n_clusters = i, random_state = 0).fit(model3_data)  # 构建并训练模型
    score = silhouette_score(model3_data, kmeans_num31.labels_)  # 轮廓系数
    silhouettteScore3.append(score)
    print('数据聚%d类silhouette_score指数为：%f'%(i,score))
    score1 = calinski_harabaz_score(model3_data, kmeans_num31.labels_)
    calinskiharabazScore3.append(score1)
    print('数据聚%d类calinski_harabaz指数为：%f'%(i, score1))

# 绘制折线图   
plt.figure(figsize=(8, 5))
plt.rcParams['font.sans-serif'] = 'SimHei'  # 显示中文
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(1, 2, 1)  # 子图
plt.plot(range(2, 12),silhouettteScore3, 'ko-', linewidth=1.5)
plt.title('轮廓系数评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.subplot(1,2,2)  
plt.plot(range(2, 12), calinskiharabazScore3, 'o-', linewidth=1.5)
plt.title('Calinski-Harabasz指标评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.savefig('../tmp/policy_holder_ysqz.jpg') 
plt.show()
plt.close


silhouettteScore4 = []  # 轮廓系数
calinskiharabazScore4 = []  # Calinski-Harabasz
for i in range(2, 12):
    kmeans_num41 = KMeans(n_clusters = i, random_state=0).fit(claim_provider.iloc[:, 2:10])  # 构建并训练模型
    score = silhouette_score(claim_provider.iloc[:, 2:10], kmeans_num41.labels_)
    silhouettteScore4.append(score)
    print('数据聚%d类silhouette_score指数为：%f'%(i,score))
    score1 = calinski_harabaz_score(claim_provider.iloc[:, 2:10],
                                    kmeans_num41.labels_)
    calinskiharabazScore4.append(score1)
    print('数据聚%d类calinski_harabaz指数为：%f'%(i,score1))

# 绘制折线图
plt.figure(figsize=(8, 5))
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(1,2,1)  # 子图
plt.plot(range(2,12),silhouettteScore4, 'ko-', linewidth=1.5)
plt.title('轮廓系数评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.subplot(1, 2, 2)  
plt.plot(range(2, 12), calinskiharabazScore4, 'o-', linewidth=1.5)
plt.title('Calinski-Harabasz指标评价法')
plt.xlabel('聚类数目')
plt.ylabel('分数')
plt.savefig('../tmp/Provider_ysqz_evaluate.jpg')
plt.show()
plt.close