条件随机场CRF（持续更新ing...）

诸神缄默不语-个人CSDN博文目录

本文是作者学习CRF后的笔记。

最近更新时间：2022.11.17
最早更新时间：2022.11.15

条件随机场CRF是适宜于顺序预测任务的判别模型，可用于命名实体识别、词性标注等。

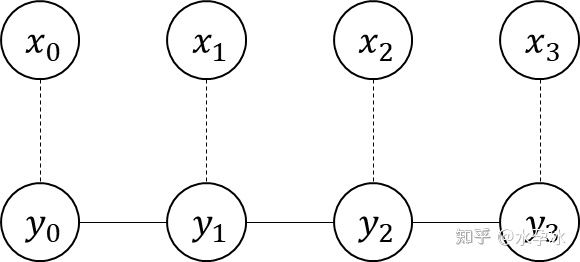
1. linear-chain CRF

在序列预测任务中，用邻近（上下文）样本来辅助学习当前样本。

以Part-of-Speech Tagging任务为例：
任务示例：输入Bob drank coffee at Starbucks，标记为Bob (NOUN) drank (VERB) coffee (NOUN) at (PREPOSITION) Starbucks (NOUN)

本节限制特征仅取决于当前和前一个标签，而非句中任一标签：

特征函数feature function$f_i$（需要一堆）：

• 输入：
  • 句子$s$
  • 词语在句中的位置$i$
  • 当前词的标签$l_i$
  • 前一个词的标签$l_{i-1}$
• 输出：实数（如0/1）

给每个feature function$f_j$分配一个权重${\lambda }_j$
给出一个句子$s$，对labeling的打分方式是对所有单词的所有feature function求和：
$$score(l|s)=\sum _{j=1}^m\sum _{i=1}^n{\lambda }_j{f}_j(s,i,l_i,l_{i-1})$$
将所有labeling的打分转换为概率（通过exponentiating and normalizing，即softmax）：
$$p(l|s)=\frac{exp[score(l|s)]}{{\sum }_{l’}exp[score(l’|s)]}=\frac{exp[{\sum }_{j=1}^m{\sum }_{i=1}^n{\lambda }_j{f}_j(s,i,l_i,l_{i-1})]}{{\sum }_{l’}exp[{\sum }_{j=1}^m{\sum }_{i=1}^n{\lambda }_j{f}_j(s,i,l{’}_i,l{’}_{i-1})]}$$

Example Feature Functions：

CRF概率长得像逻辑回归→CRF就是逻辑回归的序列版：whereas logistic regression is a log-linear model for classification, CRFs are a log-linear model for sequential labels.

CRF和HMM：

算出CRF模型后，应用在新的句子上：
原始方法——算出所有$p(l|s)$的值：太慢了
(polynomial-time) dynamic programming algorithm（由于linear-chain CRFs满足 optimal substructure 特性）（类似HMM的维特比算法）

2. CRF目标函数

在第一节中我们得到了：
$$p(l|s)=\frac{exp[{\sum }_{j=1}^m{\sum }_{i=1}^n{\lambda }_j{f}_j(s,i,l_i,l_{i-1})]}{{\sum }_{l’}exp[{\sum }_{j=1}^m{\sum }_{i=1}^n{\lambda }_j{f}_j(s,i,l{’}_i,l{’}_{i-1})]}$$

将${\sum }_{i=1}^n{f}_j(s,i,l{’}_i,l{’}_{i-1})]$记为$f_j(x,y)$（s，l）

CRF模型的定义式：
$$P(y|x)=\frac{1}{Z(x)}\exp [\sum _j{\lambda }_j(f_j(x,i))]$$
（其中$Z(x)={\sum }_y\left[{\sum }_j{\lambda }_j\right(f_j(x,i)\left)\right]$，可以看作所有可能的隐状态序列的score值之和）

我们的最终目标是找到能使得score值最大（$P(y|x)$最大）的隐状态序列。在定义好feature functions后，我们需要学习$\lambda$

用梯度学习优化feature function的权重：

1. 有一组句子-POS标签，随机初始化CRF权重
2. 梯度下降
   1. 对每个feature function $f_i$，计算样本的$\log p$关于${\lambda }_i$的梯度：$\frac{\partial }{\partial w_j}\log p(l|s)={\sum }_{j=1}^m{f}_i(s,j,l_j,l_{j-1})-{\sum }_{l’}p(l’|s){\sum }_{j=1}^m{f}_i(s,j,l{’}_j,l{’}_{j-1})$
   2. 上式第一项是$f_i$在真实标签下的贡献，第二项是在当前模型下的。（我们希望模型学到的VS模型当前状态）（其实我有点没看懂这啥意思）
   3. ${\lambda }_i={\lambda }_i+\alpha [{\sum }_{j=1}^m{f}_i(s,j,l_j,l_{j-1})-{\sum }_{l’}p(l’|s){\sum }_{j=1}^m{f}_i(s,j,l{’}_j,l{’}_{j-1})]$（$\alpha$是学习率）

本文撰写过程中使用到的其他参考资料

1. Introduction to Conditional Random Fields（一篇国内的翻译：如何轻松愉快地理解条件随机场（CRF）？ - 知乎
2. 看了一半：全网最详细的CRF算法讲解 - 知乎
3. 还没看
   1. 概率图之马尔可夫随机场（Markov Random Field，MRF）_zxhohai的博客-CSDN博客_markov random field
   2. 读懂概率图模型：你需要从基本概念和参数估计开始
   3. CRF条件随机场的原理、例子、公式推导和应用 - 知乎
   4. 全方位理解条件随机场（CRF）：原理、应用举例、CRF++实现 - 知乎
   5. 条件随机场的肤浅理解_Researcher-Du的博客-CSDN博客_densecrf论文
   6. PGM：概率图模型Graphical Model_-柚子皮-的博客-CSDN博客_graphical model
   7. 马尔可夫随机场 MRF_-柚子皮-的博客-CSDN博客
   8. 【PGM】factor graph，因子图，势函数potential function，Template models - Loull - 博客园
   9. CRF和HMM_baihaisheng的博客-CSDN博客_crf hmm
   10. CRF（条件随机场）_二叉树不是树_ZJY的博客-CSDN博客
   11. Linear-chain CRF的推导 - 简书
4. 没看懂的
   1. 条件随机场（CRF）的详细解释_deephub的博客-CSDN博客_crf
5. 排版有问题的
   1. 自然语言处理序列模型——CRF条件随机场-51CTO.COM：缺公式
   2. 条件随机场入门：有错别字