机器学习之逻辑回归中正则化——正则参数的正则约束力

机器学习之逻辑回归中正则化的正则参数

1、数据背景

​ 我们的数据来源为《吴恩达机器学期——第二周》相关数据集可在coursera当中获取下载，其课程来源为Stanford University，本篇文章中我们不会过多讲解手撸的回归算法，主要集中在正则参数对拟合结果的影响。

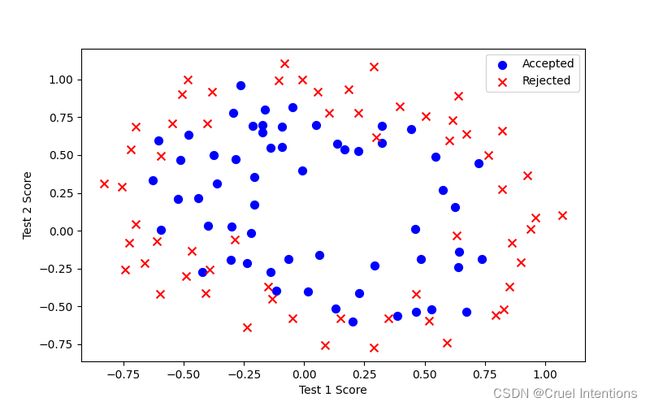
​ 设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果。对于这两次测试，你想决定是否芯片要被接受或抛弃。为了帮助你做出艰难的决定，你拥有过去芯片的测试数据集，从其中你可以构建一个逻辑回归模型。

​ 这里可以看出数据分布

2、计算方式

特征匹配扩展（feature mapping）：

​ 由于数据集中给出的特征只有两个，而我们观察数据分布发现其分布具有闭环结构，所以双特征拟合结果远远不够，所以我们进行特征映射，使之具有高阶特征属性。

​ 如果样本量多，逻辑回归问题很复杂，而原始特征只有x1,x2可以用多项式创建更多的特征x1、x2、x1x2、x1^2、x22、… X1^nX2n。因为更多的特征进行逻辑回归时，得到的分割线可以是任意高阶函数的形状，详见https://www.zhihu.com/question/65020904

假设函数：

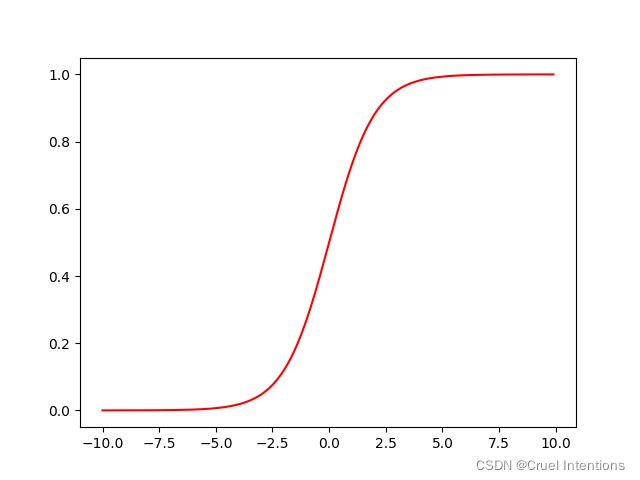
​ 我们这里采用的假设函数为sigmoid，因为我们的决策是在0~1之间的概率问题，sigmoid可以将我们的结果映射到这个区间当中。
$$h_{\theta }(x)=g({\theta }^{T}X)=\frac{1}{1+e^{-{\theta }^{T}X}}$$
​ 其标准图像如下：

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

代价函数:

​ 代价函数如下，这里要注意我们不会惩罚第一项${\theta }_0$，其作为常数特征并非系数特征

$$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n\theta {}_j{}^2$$

def cost(theta, X, y):
    first = np.multiply(-y, np.log(sigmoid(X .dot(theta.T))))
    second = np.multiply(1 - y, np.log(1 - sigmoid(X .dot(theta.T))))
    return np.mean(first - second)

def costReg(theta, X, y, l):
    #  这里注意theta0不用惩罚
    _theta = theta[1:]
    reg = (l / (2 * len(X))) * (_theta @ _theta)  # _theta@_theta == 内积
    return cost(theta, X, y) + reg

梯度下降：

​ 这里的梯度下降计算方式中我们也会引入参数的修正
$${\theta }_0={\theta }_0-a\frac{1}{m}\sum _{i=1}^m[h_{\theta }(x^{(i)})-y^{(i)}]x{}_0{}^{(i)}$$

$${\theta }_j={\theta }_j-a\frac{1}{m}\sum _{i=1}^m[h_{\theta }(x^{(i)})-y^{(i)}]x{}_j{}^{(i)}+\frac{\lambda }{m}{\theta }_j$$

​ 这里上述与${\theta }_j$相关的梯度求解我们进行调整提出可得：
$${\theta }_0={\theta }_j(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum _{i=1}^m[h_{\theta }(x^{(i)})-y^{(i)}]x{}_j{}^{(i)}$$

def gradient(theta, X, y):
    return ((sigmoid(X .dot(theta.T)) - y).dot(X)) / len(X)

def gradientReg(theta, X, y, l):
    reg = (l / len(X)) * theta
    reg[0] = 0
    return gradient(theta, X, y) + reg

L的选取：

​ 通过上述的算法函数选取我们知道在正则化的部分我们选择了正则参数来影响相关系数，这里我们将通过scipy.optimize自带的fmin_tnc优化方式来为我们进行优化拟合。

result = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, y, 1))

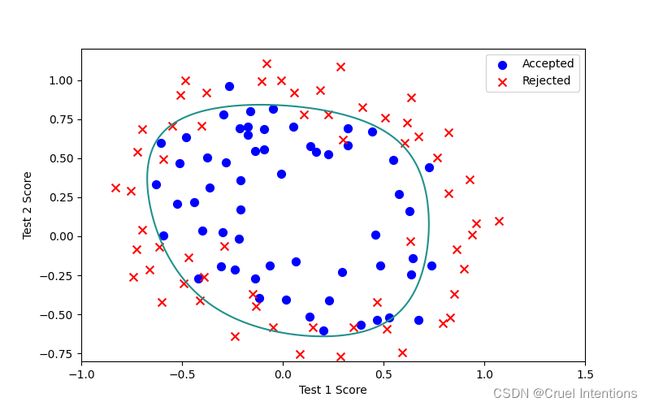
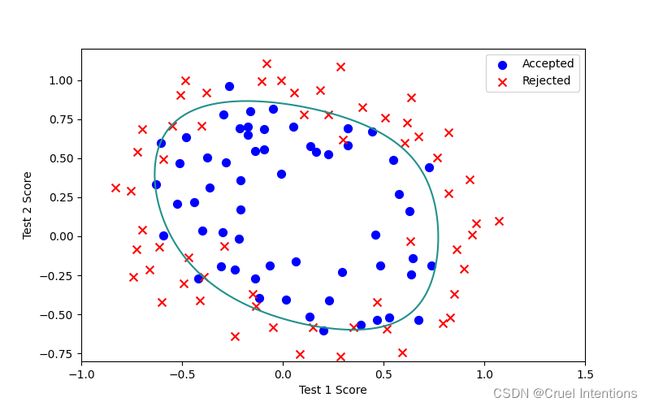
​ 其中args（）是我们传递的参数，X为原始特征，Y为相应的结果，1就是我们初始设定的L（正则化参数），由下图可见拟合效果较好。

​ L=1:

​ 我们将L更换来观察正则参数对拟合效果的影响

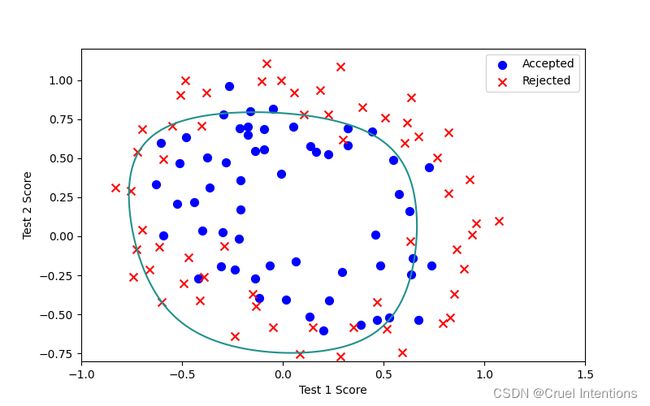
​ L=2:

​ L=10:

​ L=100:

​ L=0.2:

​ L=0.01:

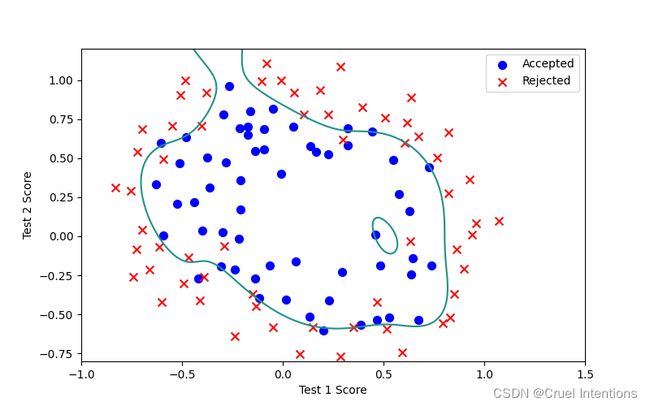
​ L=0:

​ 不难看出L在2左右的时候拟合程度较好；

​ 随着L的增大拟合程度不断变差，有上文中的公式可知，此时在拟合中我们的$\theta$就会更小，而带来的结果是拟合程度越来越差，正则化约束力过强，当L无限大时我们的曲线就变成了一条直线$y=\theta {}_0$，完全欠拟合。

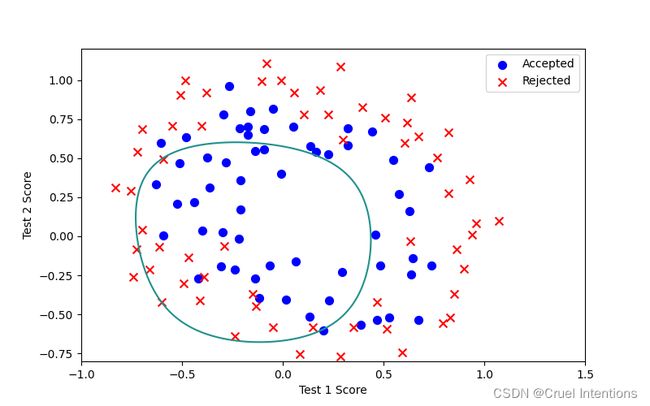
​ 但是随着L过度减小我们也发现，拟合程度越来越高，L的影响降低，正则化约束力不够，带来的结果就是出现过拟合，如图L=0所示。
总而言之正则化的作用就是为了防止在原有情况下多特征相互影响条件中的过拟合的出现。
参考链接：
blog.csdn.net/Cowry5/article/details/80247569
www.zhihu.com/question/65020904