机器学习（二）：聚类算法1——K-means算法

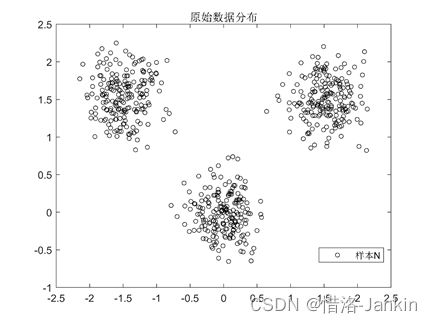
Kmeans是一种经典的聚类算法，所谓聚类，是指在没有给出目标的情况下，将样本根据某种关系分为某几类。那在kmeans中，是根据样本点间的距离，将样本n分为k个类。

K-means实现步骤：

1.首先，输入数据N并确定聚类个数K。

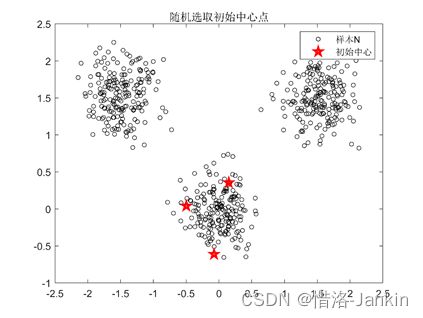
2.初始化聚类中心 ：随机选K个初始中心点。

3.计算所有样本N与K个中心点的距离，将其归到距离最近的一簇。

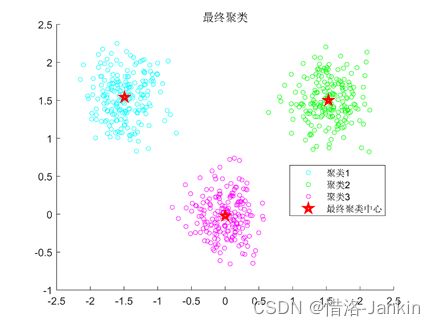
4.针对每一簇，计算该簇内所有样本到中心点距离的均值，最为新的中心点。

5.不断迭代，直到中心点不再改变或误差达到阈值。

还有一个与K-means算法非常类似的算法是K-medoids，步骤也与K-means一致，唯一的区别是k-means的中心是各个样本点的平均，可能是样本点中不存在的点。K-medoids的质心一定是某个样本点的值。

K-meansMATLAB实现：

 1.使用MATLAB自带的函数实现

idx = kmeans(X,k)               %将数据x分为k类，返回类标签
idx = kmeans(X,k,Name,Value)    %可以指定距离、使用新的初始值重复聚类的次数或使用并行计算。
[idx,C] = kmeans(___)           %返回值可以返回中心点的坐标  
[idx,C,sumd] = kmeans(___)      %返回向量中点到质心距离的簇内总和sumd      
[idx,C,sumd,D] = kmeans(___)    %返回输入矩阵中每个点到每个质心的距离D        

K-medoids自带函数实现

idx = kmedoids(X,k)
idx = kmedoids(X,k,Name,Value)
[idx,C] = kmedoids(___)
[idx,C,sumd] = kmedoids(___)
[idx,C,sumd,D] = kmedoids(___)
[idx,C,sumd,D,midx] = kmedoids(___)
[idx,C,sumd,D,midx,info] = kmedoids(___)

示例

rng('default') % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
    randn(100,2)*0.5-ones(100,2);
    randn(100,2)*0.75];
[idx,C] = kmeans(X,3);
figure
gscatter(X(:,1),X(:,2),idx,'bgm')
hold on
plot(C(:,1),C(:,2),'kx')
legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid')

2.K-means代码实现

clear all;
clc;
% 第一组数据
mu1=[0 0 ];  %均值(是需要生成的数据的均值)
S1=[.08 0 ;0 .08];  %协方差(需要生成的数据的自相关矩阵（相关系数矩阵）)
data1=mvnrnd(mu1,S1,3200);   %产生高斯分布数据
%第二组数据
mu2=[1.5 1.5 ];
S2=[.08 0 ;0 .08];
data2=mvnrnd(mu2,S2,3200);
% 第三组数据
mu3=[-1.5 1.5 ];
S3=[.08 0 ;0 .08];
data3=mvnrnd(mu3,S3,3200);
% 显示数据
plot(data1(:,1),data1(:,2),'b.');
hold on;%不覆盖原图，要关闭则使用hold off；
plot(data2(:,1),data2(:,2),'r.');
plot(data3(:,1),data3(:,2),'g.');
grid on;%显示表格
%  三类数据合成一个不带标号的数据类
data=[data1;data2;data3];
N=3;%设置聚类数目
[m,n]=size(data);%表示矩阵data大小，m行n列
pattern=zeros(m,n+1);%生成0矩阵
center=zeros(N,n);%初始化聚类中心
pattern(:,1:n)=data(:,:);

for x=1:N
    center(x,:)=data( randi(300,1),:);%第一次随机产生聚类中心
end
while 1 %循环迭代每次的聚类簇；
    distence=zeros(1,N);%最小距离矩阵
    num=zeros(1,N);%聚类簇数矩阵
    new_center=zeros(N,n);%聚类中心矩阵
    
    for x=1:m
        for y=1:N
            distence(y)=norm(data(x,:)-center(y,:));%计算到每个类的距离
        end
        [~, temp]=min(distence);%求最小的距离
        pattern(x,n+1)=temp;%划分所有对象点到最近的聚类中心；标记为1,2,3；
    end
    k=0;
    for y=1:N
        for x=1:m
            if pattern(x,n+1)==y
                new_center(y,:)=new_center(y,:)+pattern(x,1:n);
                num(y)=num(y)+1;
            end
        end
        new_center(y,:)=new_center(y,:)/num(y);%求均值，即新的聚类中心；
        if norm(new_center(y,:)-center(y,:))<0.1%检查集群中心是否已收敛。如果是则终止。
            k=k+1;
        end
    end
    if k==N
        break;
    else
        center=new_center;
    end
end
[m, n]=size(pattern);

%最后显示聚类后的数据
figure;
hold on;
for i=1:m
    if pattern(i,n)==1
        plot(pattern(i,1),pattern(i,2),'r.');
        plot(center(1,1),center(1,2),'kp');%用小圆圈标记中心点；
    elseif pattern(i,n)==2
        plot(pattern(i,1),pattern(i,2),'g.');
        plot(center(2,1),center(2,2),'kp');
    elseif pattern(i,n)==3
        plot(pattern(i,1),pattern(i,2),'c.');
        plot(center(3,1),center(3,2),'kp');
    elseif pattern(i,n)==4
        plot(pattern(i,1),pattern(i,2),'y.');
        plot(center(4,1),center(4,2),'kp');
    else
        plot(pattern(i,1),pattern(i,2),'m.');
        plot(center(4,1),center(4,2),'kp');
    end
end

3.K-means算法Python实现

Python代码来自机器学习（二）——K-均值聚类（K-means）算法 - 1ang - 博客园

#k-means算法的实现
#-*-coding:utf-8 -*-
from numpy import *
from math import sqrt


import sys
sys.path.append("C:/Users/Administrator/Desktop/k-means的python实现")
 
def loadData(fileName):
    data = []
    fr = open(fileName)
    for line in fr.readlines():
        curline = line.strip().split('\t')
        frline = map(float,curline)
        data.append(frline)
    return data
'''
#test
a = mat(loadData("C:/Users/Administrator/Desktop/k-means/testSet.txt"))
print a
'''
#计算欧氏距离
def distElud(vecA,vecB):
    return sqrt(sum(power((vecA - vecB),2)))

#初始化聚类中心
def randCent(dataSet,k):
    n = shape(dataSet)[1]
    center = mat(zeros((k,n)))
    for j in range(n):
        rangeJ = float(max(dataSet[:,j]) - min(dataSet[:,j]))
        center[:,j] = min(dataSet[:,j]) + rangeJ * random.rand(k,1)
    return center
'''
#test
a = mat(loadData("C:/Users/Administrator/Desktop/k-means/testSet.txt"))
n = 3
b = randCent(a,3)
print b
'''
def kMeans(dataSet,k,dist = distElud,createCent = randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))
    center = createCent(dataSet,k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            minDist = inf
            minIndex = -1
            for j in range(k):
                distJI = dist(dataSet[i,:],center[j,:])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i,0] != minIndex:#判断是否收敛
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist ** 2
        print center
        for cent in range(k):#更新聚类中心
            dataCent = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]]
            center[cent,:] = mean(dataCent,axis = 0)#axis是普通的将每一列相加，而axis=1表示的是将向量的每一行进行相加
    return center,clusterAssment
'''
#test
dataSet = mat(loadData("C:/Users/Administrator/Desktop/k-means/testSet.txt"))
k = 4
a = kMeans(dataSet,k)
print a
'''