吴恩达机器学习课程笔记二
文章目录
- 神经网络基础知识
- 神经网络前向传播
-
- 伪代码
- 前向传播中单个神经元的作用
- 矩阵加速运算
- 训练模型的细节
- 常用激活函数
-
- ReLU
- Sigmoid
- Linear activation function
- tanh
- 选择激活函数
-
- 选择`输出层`的激活函数
- 选择`隐藏层`的激活函数
- 为什么需要非线性激活函数
- Softmax激活函数
- 多标签分类问题
- 梯度下降更好训练神经网络的方式-Adam
神经网络基础知识
neuron:神经元
activation:激活
layer:层(一组神经元)
hidden layer :隐藏层
output layer :输出层
数据量增大时,传统机器学习、小型神经网络、中型神经网络、大型神经网络的的性能变化,在大数据的今天一定要学深度学习
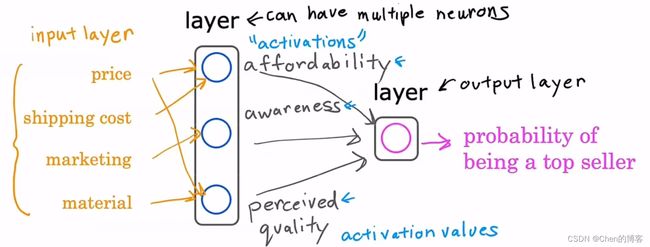
神经网络一层(layer)由一个或者多个神经元构成
每一层的输出值也称为激活值(activate)
第一层的输入特征也被称为输入层
最后一层为输出层
在构建大型神经网络时,我们不可能手动将特征连接到神经元,一般是下图这样
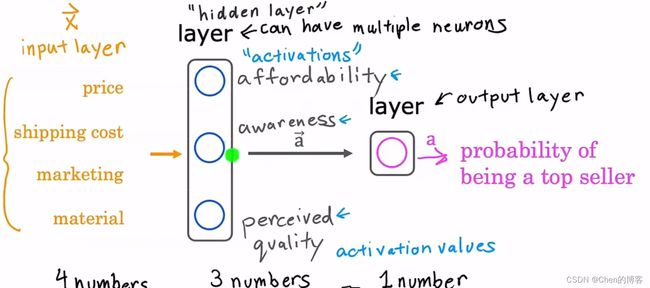
也可以是下图这样
中间的这一层三个神经元的也被称为隐藏层
通常说几层神经网络时,包括最后一层输出层,但是不包括第0层输入层
第i层的输出的激活值写做 a [ i ] a^{[i]} a[i]
所以上图中layer 4省略的为: a 2 [ 3 ] = g ( w [ 3 ] ∗ a [ 2 ] + b [ 3 ] ) a^{[3]}_2=g(w^{[3]}*a^{[2]}+b^{[3]}) a2[3]=g(w[3]∗a[2]+b[3])
神经网络前向传播
前向传播:神经元产生激活值传播给向下一层的神经元,作为下一层神经元输入值
伪代码
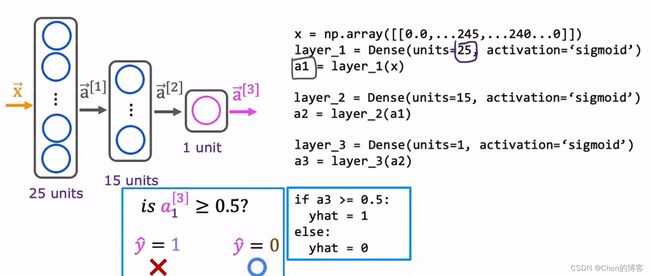
layer 1有25个神经元,layer 2有15个神经元,layer 3 有一个神经元
简化代码:
进一步简化代码:
使用Tensorflow或者Pytorch能简便构建和训练神经网络,不过不能只会用,要弄懂这些代码在干些什么!
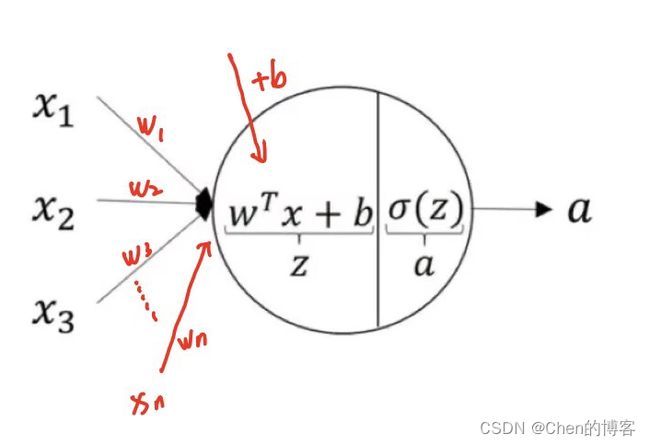
前向传播中单个神经元的作用
上图为layer n的神经元,接受layer n-1的激活值 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn乘于权重加上偏置 b b b,传入激活函数中,得到这个神经元的激活值 a a a
左侧代码为单个隐藏层的实现代码,右侧为整个四层的神经网络实现代码
矩阵加速运算
将左侧的代码中的输入数据 X X X和偏置 b b b都改为矩阵的形式,再利用矩阵相关加速运算
训练模型的细节
训练模型的步骤:
1定义模型
2.定义损失函数
3.最小化损失函数
中间为手写字体识别只包含0,1,的二分类,使用sigmoid激活函数,使用二元交叉熵作为损失函数
右侧为在Tensorflow中训练这个模型的步骤
常用激活函数
ReLU
ReLU全名Rectified Linear Unit,意思是修正线性单元。
ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变,这种操作被成为单侧抑制
ReLU激活函数可写为: R e L U ( z ) = m a x ( 0 , z ) ReLU(z)=max(0,z) ReLU(z)=max(0,z)
Sigmoid
Sigmoid激活函数可写为: S i g m o i d ( z ) = 1 1 + e − z Sigmoid(z)=\frac{1}{1+e^{-z}} Sigmoid(z)=1+e−z1
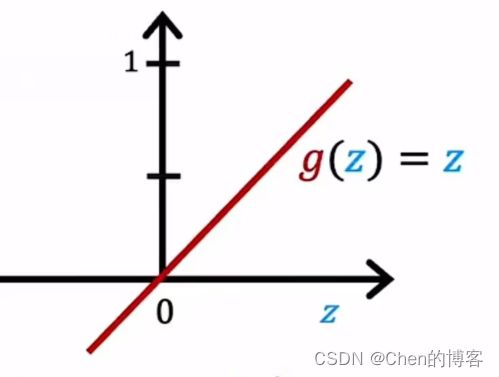
Linear activation function
线性激活函数可写为: g ( z ) = z g(z)=z g(z)=z
tanh
tanh激活函数可写为: g ( z ) = 1 − e − 2 x 1 + e − 2 x g(z)=\frac{1-e^{-2x}}{1+e^{-2x}} g(z)=1+e−2x1−e−2x
选择激活函数
可以为神经网络中的神经元选择不同的激活函数
选择输出层的激活函数
二分类问题选择Sigmoid激活函数作为输出层的激活函数
回归问题选择线性激活函数作为输出层的激活函数
如果回归问题结果非负可以选择ReLU激活函数作为输出层的激活函数
选择输出层的激活函数时,通常根据输出的预测值 y ^ \hat{y} y^来选择
选择隐藏层的激活函数
ReLU激活函数是现在神经网络中隐藏层最常用的激活函数
为什么需要非线性激活函数
如果神经网络使用的激活函数都是线性的,那么神经网络就只是线性回归模型,神经网络无法拟合比线性回归更复杂的模型
Softmax激活函数
Softmax是Sigmoid的推广,可以进行多分类任务
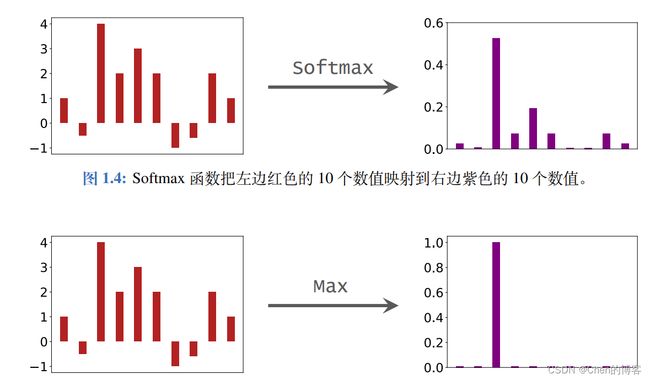
Softmax 激活函数:
将输入向量的值映射到(0,1)这个区间,转化为概率的形式,且转化后向量元素和为1,公式为:
向 量 A = [ a 1 , a 2 , a 3 . . . a 4 ] T s o f t m a x ( a i ) = e a i ∑ j = 1 k e a i 例 如 : 假 设 向 量 a = [ 3.2 , 5.1 , − 5.7 ] T 经 过 函 数 运 算 后 a s o f t m a x = [ 0.127 , 0.87 , 0.003 ] T 向量A=[a_1,a_2,a_3...a_4]^T\\ softmax(a_i)=\frac{e^{a_i}}{\sum_{j=1}^ke^{a_i}}\\\\ 例如: 假设向量a=\left[\ \ 3.2,\ \ 5.1,-5.7\ \ \right]^T\\ 经过函数运算后a_{softmax}=\left[\ \ 0.127,\ \ 0.87,\ \ 0.003\ \ \right]^T\\ 向量A=[a1,a2,a3...a4]Tsoftmax(ai)=∑j=1keaieai例如:假设向量a=[ 3.2, 5.1,−5.7 ]T经过函数运算后asoftmax=[ 0.127, 0.87, 0.003 ]T
可以看出softmax激活函数的特性:让小的值变得很小,最大的值变得更大,使得分类效果更加明显更加利于分类
突出了最大值
多标签分类问题
多标签分类,与一般的多分类问题不同,一般的多分类问题,如手写字识别,其真正的标签只有一个,而多标签分类,如下图的人、汽车、公共汽车识别,识别出的结果可能有多个
如何解决多分类问题:以上图为例子
1.可以将其视为三个完全独立的机器学习问题,需要三个神经网络分别检测
2.训练一个神经网络同时检测这人、汽车、公共汽车
梯度下降更好训练神经网络的方式-Adam
w j = w j − α ∂ ∂ w j J ( W ⃗ , b ) w_j=w_j-\alpha\frac{\partial}{\partial w_j}J(\vec{W},b) wj=wj−α∂wj∂J(W,b)
Adam算法,当学习率过小时可以自动增加 α \alpha α使得梯度下降的速度更快;
当学习率过大时,也可以使得学习率自动更小。
Adam算法可以自动调整学习率
Adam算法没有使用单一的全局学习率,对模型的每个参数使用不同的学习率如下图: