动态规划---图像压缩
动态规划---图像压缩
- 问题描述
- 分析
- 代码如下
- 运行结果如下
-
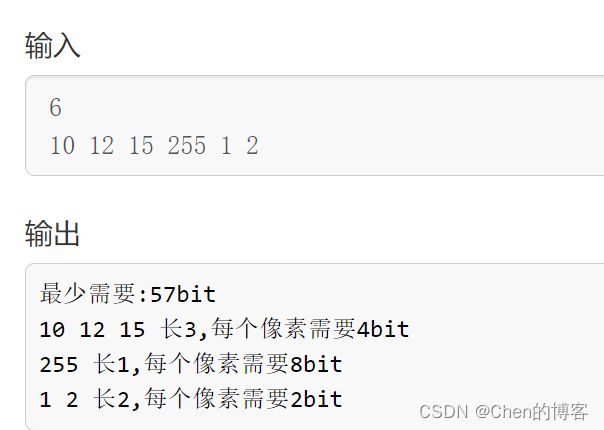
- 结果一
- 结果二
在算法课上遇到这个图像压缩这个问题,可以用
动态规划来求解,之前没有遇到过这个问题,在网上查找相关的题解也比较少,就写一下自己的理解。
问题描述
一幅图像的由很多个像素点构成,像素点越多分辨率越高,像素的灰度值范围为0~255,
也就是需要8bit来存储一个像素的灰度值信息。
一幅由n*m像素点构成的图像,所需存储空间大小为:n*m*8bit=8nmbit(这是非常大的,直接传输很慢)
然而,正常情况下,一幅图像的某一范围内像素点的灰度值是很接近的,表现为一幅图片某一区域颜色相近。
例如,一个像素灰度值序列P={1,2,2,2,1,2,60,55,78}(传输过程中把图像像素点转成序列,
而不是直接传输矩阵),每个像素灰度值都用8bit来存储是非常消耗空间的,例如:
直接存储: 9*8bit=72bit,这是非常不划算的,我们想要无损压缩图片。
即:
将像素序列分段,段内的像素灰度值相似(可以用小于8bit的空间来存储一个像素灰度值),
一段内的像素用相同的bit数来存储,只需要额外存树每段的长度和bit数即可,这样可以节省很多空间。
b[i]:第i段中每个像素的位数,1<=b[i]<=8,需要3 bit
l[i];第i段中像素的个数,1<=l[i]<=255,需要8 bit
所以每一段需要额外的 3+8=11 bit来存储段内像素的信息
分析
如何分段?
若分为 m 段,则需要的存储总位数为 : ∑ i = 1 m b [ i ] ∗ l [ i ] + m ∗ 11 若分为m段,则需要的存储总位数为: \sum_{i=1}^{m}b[i]*l[i]+m*11 若分为m段,则需要的存储总位数为:i=1∑mb[i]∗l[i]+m∗11
考虑用动态对规划来求解问题:
最优子结构 : p 1 , p 2 , p 3 , . . . . p m 考虑最后一个分段为 l [ m ] 个元素 p n − l [ m ] + 1 ∼ p [ n ] , 则子问题为 p 1 ∼ p [ l [ m ] ] 的分段 ( 前 m − 1 段 ) 子问题的最优解为 b [ i ] , l [ i ] , 1 < = i < = m − 1 最后一个分段最优和前 m − 1 个分段最优构成了原问题分段最优,最优子结构存在 在求解第 i 段过程中需要前 i − 1 段分法的信息,存在重复子问题可以用动态规划的思想来求解问题 最优子结构:\\ {p1,p2,p3,....pm}\\ 考虑最后一个分段为l[m]个元素\\ p_{n-l[m]+1}\sim p[n],\\ 则子问题为p_1\sim p[l[m]]的分段(前m-1段)\\ 子问题的最优解为b[i],l[i],1<=i<=m-1\\ 最后一个分段最优和前m-1个分段最优构成了原问题分段最优,最优子结构存在\\ 在求解第i段过程中需要前i-1段分法的信息,存在重复子问题 可以用动态规划的思想来求解问题 最优子结构:p1,p2,p3,....pm考虑最后一个分段为l[m]个元素pn−l[m]+1∼p[n],则子问题为p1∼p[l[m]]的分段(前m−1段)子问题的最优解为b[i],l[i],1<=i<=m−1最后一个分段最优和前m−1个分段最优构成了原问题分段最优,最优子结构存在在求解第i段过程中需要前i−1段分法的信息,存在重复子问题可以用动态规划的思想来求解问题
状态表示:
f[i]表示以A[i](包含)结尾的最优分段所需的bit数(最少)
状态转移:
f[i] =A[i-k]+bitmax(i-k+1,i)+11 , 0<=k<=i
bitmax(i-k+1,i)为求i-k+1到i这个序列每个像素灰度值需要的的bit数
其中,k<=256(图像压缩的限制)
f[i] =A[i-k]+bitmax(i-k+1,i)+11 , 0<=k<=min(i,256)
时间复杂度分析:
遍历序列n,
遍历(i-k+1,i)
求bitmax(i-k+1,i)
时间复杂度看起来是O(n^3)
但是k<=256,所以时间复杂度为O(n) (n前常数会比较大)
代码如下
#include