机器学习-22：MachineLN之RL

你要的答案或许都在这里：小鹏的博客目录

我想说：

其实很多事情找对方法很重要，可以事半功倍，就好比学习；

原本打算将机器学习基础写完以后再写深度学习、强化学习、迁移学习的内容，但是现在看还是中间穿插一点比较好。

看一下强化学习入门的一点东西，从概念说起吧：下面基本是在挖坑，后面会慢慢填起来。

其实机器学习可以大致分为三类：监督学习、非监督学习、强化学习；

强化学习是一个很重要的分支，目前来说比较火；

1. 什么是强化学习：

强化学习：它关注的是智能如何在环境中采取一系列行为，从而获得最大的累计回报，通过比较来更深刻的理解一下：

增强学习和监督学习的主要区别：

• 增强学习是试错学习，由于没有直接的指导信息，智能体要以不断与环境进行交互，通过试错的方式来获得最佳的策略；

• 延迟回报， 增强学习的指导信息很多， 而且往往是在事后（最后一个状态）才给出的，这就导致了一个问题，就是获得正报或者负报以后，如何将回报分配给前面的状态。

不明白不要紧，慢慢来，看个例子：

假设我们要构建一个下国际象棋的机器，这种情况不能使用监督学习，首先，我们本身不是优秀的棋手，而请象棋老师来遍历每个状态下的最佳棋步则代价过于昂贵。其次，每个棋步好坏判断不是孤立的，要依赖于对手的选择和局势的变化。是一系列的棋步组成的策略决定了是否能赢得比赛。下棋过程的唯一的反馈（在强化学习中这个反馈就是得到的奖励或者惩罚，也就是说延迟回报，并不是实时的，也可以理解为不以一时成败论英雄，只看最后，当然高手们对决几步就可能看出最终的胜负，你这么想问题又来了，你的AI思维哪去了？并不要想当然）是在最后赢得或是输掉棋局时才产生的。这种情况我们可以采用增强学习算法，通过不断的探索和试错学习，增强学习可以获得某种下棋的策略，并在每个状态下都选择最有可能获胜的棋步。目前这种算法已经在棋类游戏中得到了广泛应用。

2. 马尔可夫决策过程（MDP）

学习强化学习不得不知的马尔科夫决策过程：

一个马尔可夫决策过程由一个四元组构成M = (S, A, P_sa, ?) 

• S: 表示状态集(states)，有s∈S，s_i表示第i步的状态。

• A:表示一组动作(actions)，有a∈A，a_i表示第i步的动作。

• ?_sa: 表示状态转移概率。?_s? 表示的是在当前s ∈ S状态下，经过a动作 ∈ A作用后，会转移到的其他状态的概率分布情况。比如，在状态s下执行动作a，转移到s'的概率可以表示为p(s'|s,a)。

• R: S×A⟼ℝ ，R是回报函数(reward function)。有些回报函数状态S的函数，可以简化为R: S⟼ℝ。如果一组(s,a)转移到了下个状态s'，那么回报函数可记为r(s'|s, a)。如果(s,a)对应的下个状态s'是唯一的，那么回报函数也可以记为r(s,a)。

上面的组成有了，那么我们让这些组合在一起想去做一件什么事情呢？其实最终的目的就是，知道现在的位置如何最快的到达目的地（达到目标），这个最快我们在这里使用回报来衡量的，也可以描述为获得的回报最大。这个是我们最终想要学习的东西，中间的过程是怎么做的？ 了解过强化学习的应该知道算法：Sarsa和Q-learning：（跳跃有点快？有坑不要紧：学习就是挖坑和填坑的过程，这和强化学习的思想差不多，我也没必要万事俱备了再去做一些事情，可以不断的探索和试错学习，已经挖了很多坑，后面慢慢填起来）

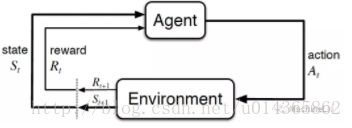
再看一下图，可以得到大致流程：开始agent（Q表）随机一个state和action，给env，env给予反馈，得到下一个状态和奖励，更新agent，之后agent在根据这个状态和奖励作出下一步行动，再给env，一次迭代进化。

Sarsa：

Q-learning：

上代码：先带带感觉：

Sarsa：

import numpy as np
import pandas as pd
import time
np.random.seed(2)  # reproducible
# 定义6种状态
N_STATES = 6   
# 在线性状态下只能采取往左或者往右
ACTIONS = ['left', 'right']     
EPSILON = 0.9   # greedy police
# 学习率
ALPHA = 0.1   
# 随机因素， 我们有10%的可能随便选取行动  
GAMMA = 0.9    
# 我们的智能体， 进化次数
MAX_EPISODES = 13   
# 为了防止太快，方便观看，sleep一下
FRESH_TIME = 0.3   
# Q表用来记录每种状态采取的行动回报值。
# 下面是进行初始化；
def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),   # 初始化奖励值
        columns=actions,   # 采取的行动
    )
    # print(table)    
    return table
# 根据Q表，获取目前状态下采取的行动， 注意有10%的随机性
def choose_action(state, q_table):
    # 获得在某状态下的奖励， 但是如何行动的话，怎么选择？
    # 两种方式：（1）10%的随机；（2）选取回报最大的作为下一步的行动；
    state_actions = q_table.iloc[state, :]
    if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()): 
        action_name = np.random.choice(ACTIONS)
    else:   # act greedy
        action_name = state_actions.idxmax()    
    return action_name
# 根据行动后，所在的状态给予奖励；
def get_env_feedback(S, A):
    # 这里智能体就会得到反馈；
    # 往右移动
    if A == 'right':   
        # 这就是延时回报的原因，开始进化时只有到了最后我们才知道是否应该给予奖励
        if S == N_STATES - 2:   
            S_ = 'terminal'
            R = 1
        # 下面虽然没有给予奖励，但是状态加一，也就是说目的地更近了一步，也算是一种奖励
        else:
            S_ = S + 1
            R = 0
    # 那么如果你往左，下面都是惩罚
    else:   
        R = 0
        if S == 0:
            S_ = S 
        else:
            S_ = S - 1
    return S_, R
# 用来更新目前的结果 和 现实
def update_env(S, episode, step_counter):
    env_list = ['>>>']*(N_STATES-1) + ['OK'] 
    if S == 'terminal':
        interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
        print('\r{}'.format(interaction), end='')
        time.sleep(2)
        print('\r                                ', end='')
    else:
        env_list[S] = 'ooo'
        interaction = ''.join(env_list)
        print('\r{}'.format(interaction), end='')
        time.sleep(FRESH_TIME)
# 下面就是智能体核心进化流程， 也就是一个算法的优化流程；
def rl():
    # 初始化Q表
    q_table = build_q_table(N_STATES, ACTIONS)
    # 智能体进化次数
    for episode in range(MAX_EPISODES):
        step_counter = 0
        # 状态从0开始；
        S = 0
        # 行动往左开始；
        A = 'left'
        # 一个标示， 表示是否到达终点。
        is_terminated = False
        # 更新显示
        update_env(S, episode, step_counter)
        # 如果智能体没有到达目的地， 不停的迭代
        while not is_terminated:
            # 根据此时状态和采取的行动， 得到下一个所在的状态和应得奖励
            S_, R = get_env_feedback(S, A)  
            # 判断上面采取行动A后是否到达目的地； 如果没有，此时再此状态从Q表获得下一步的行动；
            if S_ != 'terminal':
                A_ = choose_action(S_, q_table)
            # 获得S状态A行动下的回报值，这里是后面此时Q表的更新；
            q_predict = q_table.loc[S, A]
            # Sarsa算法的精髓
            if S_ != 'terminal':
                q_target = R + GAMMA * q_table.loc[S_, A_] #.max()   # next state is not terminal
            # 达到目的地获得奖励， 回报给上一个状态动作哦， 就是这样回传的。
            else:
                q_target = R     
                is_terminated = True    
            # 更新
            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  
            S = S_  
            A = A_
            print (S, A)
            update_env(S, episode, step_counter+1)
            step_counter += 1
            print (q_table)
    return q_table
if __name__ == "__main__":
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

Q-learning：

将rl()换成这个：

def rl():
    # main part of RL loop
    q_table = build_q_table(N_STATES, ACTIONS)
    for episode in range(MAX_EPISODES):
        step_counter = 0
        S = 0
        is_terminated = False
        update_env(S, episode, step_counter)
        while not is_terminated:
            A = choose_action(S, q_table)
            S_, R = get_env_feedback(S, A)  # take action & get next state and reward
            q_predict = q_table.loc[S, A]
            if S_ != 'terminal':
                q_target = R + GAMMA * q_table.iloc[S_, :].max()   # next state is not terminal
            else:
                q_target = R     # next state is terminal
                is_terminated = True    # terminate this episode
            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  # update
            S = S_  # move to next state
            update_env(S, episode, step_counter+1)
            step_counter += 1
    return q_table

推荐阅读：

1. 机器学习-1：MachineLN之三要素

2. 机器学习-2：MachineLN之模型评估

3. 机器学习-3：MachineLN之dl

4. 机器学习-4：DeepLN之CNN解析

5. 机器学习-5：DeepLN之CNN权重更新（笔记）

6. 机器学习-6：DeepLN之CNN源码

7. 机器学习-7：MachineLN之激活函数

8. 机器学习-8：DeepLN之BN

9. 机器学习-9：MachineLN之数据归一化

10. 机器学习-10：MachineLN之样本不均衡

11. 机器学习-11：MachineLN之过拟合

12. 机器学习-12：MachineLN之优化算法

13. 机器学习-13：MachineLN之kNN

14. 机器学习-14：MachineLN之kNN源码

15. 机器学习-15：MachineLN之感知机

16. 机器学习-16：MachineLN之感知机源码

17. 机器学习-17：MachineLN之逻辑回归

18. 机器学习-18：MachineLN之逻辑回归源码

19. 机器学习-19：MachineLN之SVM（1）

20. 机器学习-20：MachineLN之SVM（2）

21. 机器学习-21：MachineLN之SVM源码