朴素贝叶斯算法原理、代码实现原理、以及鸢尾花分类代码实现(详细代码原理讲解)
朴素贝叶斯算法原理及鸢尾花分类代码实现
一、概率模型
1、全概率公式(由因推果)
设事件B1,B2,…,Bn构成一个完备事件组,即两两不相容,和为全集且P(Bi)>0,则对任意事件A,有
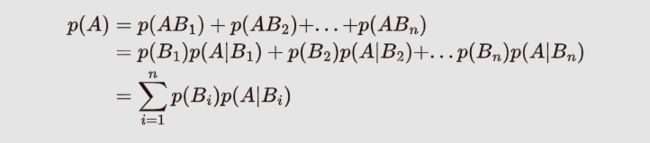
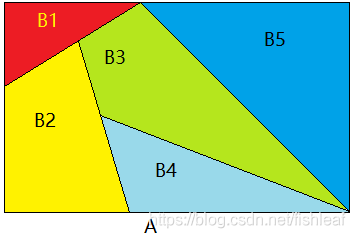
由因推果的理解:如上图:可以理解为A事件的发生是由 B 1 , B 2 . . . . B 5 B_1,B_2....B_5 B1,B2....B5这些原因导致的,有: p ( A ) = p ( A B 1 ) + p ( A B 2 ) + . . . + p ( A B n ) p(A) = p(AB_1)+p(AB_2)+...+p(AB_n) p(A)=p(AB1)+p(AB2)+...+p(ABn),再由条件概率公式即可推导出全概率公式。
2、贝叶斯公式(由果溯因)
二、在机器学习中的应用(朴素贝叶斯算法)
1、贝叶斯公式在机器学习分类问题中的形式:
p ( y i ∣ x ) = p ( y i ) p ( x ∣ y i ) ∑ i = 1 n p ( y i ) p ( x ∣ y i ) p(y_i|x)=\frac{p(y_i)p(x|y_i)}{\sum_{i=1}^{n}{p(y_i)p(x|y_i)}} p(yi∣x)=∑i=1np(yi)p(x∣yi)p(yi)p(x∣yi)
因为朴素贝叶斯假设数据的各个特征之间是彼此独立的:
所以有: p ( x ∣ y i ) = p ( x 1 ∣ y i ) p ( x 2 ∣ y i ) p ( x 3 ∣ y i ) . . . p ( x n ∣ y i ) p(x|y_i)=p(x_1|y_i)p(x_2|y_i)p(x_3|y_i)...p(x_n|y_i) p(x∣yi)=p(x1∣yi)p(x2∣yi)p(x3∣yi)...p(xn∣yi)
故朴素贝叶斯公式为:
p ( y i ∣ x ) = p ( y i ) ∏ j = 1 n p ( x j ∣ y i ) ∑ i = 1 n p ( y i ) ∏ j = 1 n p ( x j ∣ y i ) p(y_i|x)=\frac{p(y_i)\prod_{j=1}^{n}{p(x_j|y_i)}}{\sum_{i=1}^{n}{p(y_i)\prod_{j=1}^{n}{p(x_j|y_i)}}} p(yi∣x)=∑i=1np(yi)∏j=1np(xj∣yi)p(yi)∏j=1np(xj∣yi)
当用于分类问题时, Y p r e d = a r g m a x P ( y i ∣ x ) Y_{pred}=argmax{P(y_i|x)} Ypred=argmaxP(yi∣x) ,由于 p ( y i ∣ x ) p(y_i|x) p(yi∣x)的分母都是相同的,所以只需要求分子的最大值来判断分类结果,即就是: Y p r e d = a r g m a x P ( y i ) ∏ j = 1 n P ( x j ∣ y i ) Y_{pred}=argmax{P(y_i)\prod_{j=1}^{n}{P(x_j|y_i)}} Ypred=argmaxP(yi)∏j=1nP(xj∣yi),注意:在代码中往往将连乘用log函数转换为相加。由此,只需要计算先验概率: p ( y i ) p(y_i) p(yi)和似然度: p ( x j ∣ y i ) p(x_j|y_i) p(xj∣yi)。
三、3种常见的朴素贝叶斯模型(三种计算先验概率和似然度的方法)
1、高斯分布模型
适用:数据集的特征时连续型数据时
先 验 概 率 : p ( y i ) = N y i N 后 验 概 率 : p ( x j ∣ y i ) = 1 δ 2 π e − ( x j − y i ) 2 δ j 2 先验概率: p(y_i)=\frac{N_{y_i}}{N}\\ 后验概率:p(x_j|y_i)=\frac{1}{\delta\sqrt{2\pi}}e^{-\frac{(x_j-y_i)}{2\delta_j^2}} 先验概率:p(yi)=NNyi后验概率:p(xj∣yi)=δ2π1e−2δj2(xj−yi)
其中 N y i N_{y_i} Nyi是训练样本中类别为 y i y_i yi的样本的个数,N为训练样本的总个数。
2、多项式模型
适用:数据集的特征为离散型
先 验 概 率 : p ( y i ) = N y i + α N + k α 后 验 概 率 : p ( x j ∣ y i ) = N y i , x j + α N y j + n α 注 : 其 中 α 是 平 滑 因 子 , 防 止 后 验 概 率 为 0 , N y i , x j 是 类 别 为 y i 的 样 本 中 , 第 j 维 度 的 特 征 为 x j 先验概率:p(y_i)=\frac{N_{y_i}+\alpha}{N+k\alpha}\\ 后验概率:p(x_j|y_i)=\frac{N_{y_i,x_j}+\alpha}{N_{y_j}+n\alpha}\\ 注:其中\alpha是平滑因子,防止后验概率为0,N_{y_i,x_j}是类别为y_i的样本中,第j维度的特征为x_j 先验概率:p(yi)=N+kαNyi+α后验概率:p(xj∣yi)=Nyj+nαNyi,xj+α注:其中α是平滑因子,防止后验概率为0,Nyi,xj是类别为yi的样本中,第j维度的特征为xj
3、伯努利模型
**使用:数据集的特征为bool类型,即特征的值只能取0或者1
当 x j = 1 时 : p ( x j ∣ y i ) = p ( x j = 1 ∣ y i ) 当 x j = 0 时 : p ( x j ∣ y i ) = p ( x j = 0 ∣ y i ) 当x_j=1时:p(x_j|y_i)=p(x_j=1|y_i)\\ 当x_j=0时:p(x_j|y_i)=p(x_j=0|y_i) 当xj=1时:p(xj∣yi)=p(xj=1∣yi)当xj=0时:p(xj∣yi)=p(xj=0∣yi)
鸢尾花分类代码实现
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
X = iris.data
Y = iris.target
# 分割训练集和验证集
x_train,x_test,y_train,y_test = train_test_split(X,Y,random_state=4)
print(len(x_train))
print(len(x_test))
print(len(y_train))
print(len(y_test))
# 计算每一类的先验概率,以及每一类中每一种特征的均值和方差
def prior_Mean_Var(x_train,y_train):
prior_list=[]
mean = np.array([[0,0,0,0]])
var = np.array([[0,0,0,0]])
for kind in range(3):
x_class = x_train[np.nonzero(kind==y_train)]
prior_list.append(len(x_class)/len(x_train))
m = np.mean(x_class,axis=0,keepdims=True)
mean = np.append(mean,m,axis=0)
v = np.var(x_class,axis=0,keepdims=True)
var = np.append(var,v,axis=0)
return prior_list,mean[1:],var[1:]
# 对样本进行分类
def predict(x_test,y_test,prior,mean,var):
# 防止分母为0
_class = []
eps = 1e-10
for i in x_test:
x = np.tile(i,(3,1))
p = (np.exp(-(x-mean)**2/(2*var+eps)))/(np.sqrt(2*np.pi)*var+eps)
# 每个类别对应的后验概率,p(x/yi)
p_after = np.sum(np.log(p),axis=1)
p_class = np.log(prior)+p_after
_class.append(np.argmax(p_class))
return _class
prior,mean,var=prior_Mean_Var(x_train,y_train)
y_pred = predict(x_test,y_test,prior,mean,var)
# 计算模型的准确率:
count=0
for i in range(len(y_test)):
if(y_pred[i]==y_test[i]):
count=count+1
accuracy = count/len(y_test)
print('accuracy: {:.2%}'.format(accuracy))
