Gurobi求解器基础入门官方教程

（一）基础操作

1.Gurobi简介

Gurobi是一种数学规划（线性和凸二次规划）优化器。支持多种语言接口，本文以python+gurobi为主。

2.Gurobi扩展包

在建模过程中，经常要对带下标数据做挑选，不同下标的数据进行组合，使用python原本处理数据的list,tuple,dict会面临效率问题，因此Gurobi 中采用了特殊的扩展对象 TupleList 和 TupleDict

（1）Gurobi tuplelist

tuplelist增加了快速筛选select功能，例如从cities中找到第一个元素为A的元组

from gurobipy import *
cities = [('A','B'), ('A','C'), ('B','C'),('B','D'),('C','D')]
routes = tuplelist(cities)
print(routes.select('A','*'))

<gurobi.tuplelist (2 tuples, 2 values each):
 ( A , B )
 ( A , C )

等效于下面的代码

result = []
for i,j in cities:
    if i == 'A':
        result.append((i,j))
print(result)

[('A', 'B'), ('A', 'C')]

（2）Gurobi tupledict

键值为 tuple （元组），可以使用 select, sum, prod 函数
用于变量和约束（后面案例中体现）

• sum()函数：变量求和

import gurobipy as gp
from gurobipy import *
m = gp.Model("ooo")
x = m.addVars(3,4,vtype=GRB.BINARY,name='x')
m.addConstrs((x.sum(i,'*')<=1 for i in range(3)),name='con')
m.update()

语句m.addConstrs((x.sum(i,'*')<=1 for i in range(3)),name='con')产生如下约束，对于每个i和要小于1

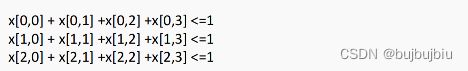
• prod()函数：用于变量和系数相乘后累加

下面两个表达式等效，即变量x和系数cost想乘后累加

obj = quicksum(cost[i,j]*x[i,j] for i,j in arcs)
obj = x.prod(cost)

（3）Multidict()

创建 tuplelist 和 tupledict 的便捷方法，如下返回cities(tuplelist),supply(tupledict),demand(tupledict)

cities,supply,demand = multidict({'a':[100,20],'b':[150,50],
                                  'c':[20,300],'d':[10,200]})
print(cities)
print(supply)
print(demand)

['a', 'b', 'c', 'd']
{'a': 100, 'b': 150, 'c': 20, 'd': 10}
{'a': 20, 'b': 50, 'c': 300, 'd': 200}

（4）创建list

a=[]
a.append('a') # ['a']

b=[i**2 for i in range(6)] # [0, 1, 4, 9, 16, 25]

c=[(i,j) for j in range(4) for i in range(j)] # [(0, 1), (0, 2), (1, 2), (0, 3), (1, 3), (2, 3)]

d=[i for i in range(10) if i not in b] # [2, 3, 5, 6, 7, 8]

p=[]
for j in range(4):
    for i in range(j):
        p.append((i,j)) # [(0, 1), (0, 2), (1, 2), (0, 3), (1, 3), (2, 3)]

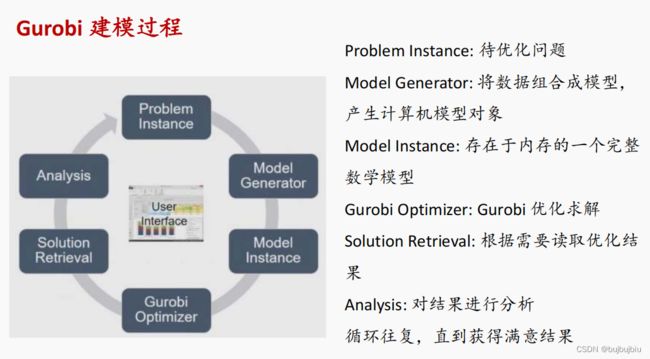
3.Gurobi建模过程

• 全部变量：addVar(),addVars()
• 目标函数：setObjective()
• 约束条件：addConstr(),addConstrs()
• 运行优化：optimize()
  
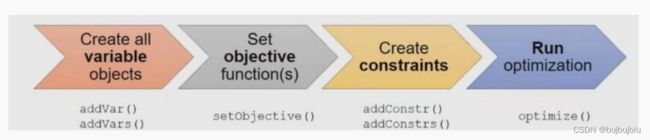
  采用 tuplelists 筛选和指定合适的下标组合关系；基于这些组合关系建立变量和数据字典；利用 tuplelist.select() 以及 tupledict.select(), tupledict.sum(), tupledict.prod() 来对下标进行组合处理

4.整数规划案例

max x+y+2z
s.t x+2y+3z<=4
    x+y>=1

from gurobipy import *
try:
    m = Model('mip')
    
    # 添加变量，GRB.BINARY表示0-1变量
    x = m.addVar(vtype=GRB.BINARY, name='x')
    y = m.addVar(vtype=GRB.BINARY, name='y')
    z = m.addVar(vtype=GRB.BINARY, name='z')
    
    # 目标函数，GRB.MAXIMIZE表示最大化
    m.setObjective(x+y+2*z, GRB.MAXIMIZE)
    
    # 约束条件
    m.addConstr(x+2*y+3*z<=4, 'c0')
    m.addConstr(x + y >= 1, 'c1')
    
    # 优化器
    m.optimize()

    # 输出变量名，取值以及目标函数值
    for v in m.getVars():
        print(f'变量名：{v.varName},取值：{v.x}')
    print(f'目标值：{m.objval}')
except GurobiError as e:
    print('error code'+str(e.errno)+':'+str(e))
except AttributeError:
    print('encountered an attribute error')

变量名：x,取值：1.0
变量名：y,取值：0.0
变量名：z,取值：1.0
目标值：3.0

（二）功能和操作进阶

1. 重要参数和属性

（1）参数和属性功能

• Parameter(参数)：控制优化器的行为，需要在优化启动前设置。
  例如：控制求解时间 TimeLimit，控制控制台输出log记录LogToConsole
• Attributes(属性)：控制模型（模型，变量，约束，目标等对象）的特征
  例如：模型ModelSense，变量LB/UB，约束RHS

（2）参数类别

• Termination 停止参数：控制求解停止条件
  例如：TimeLimit 设定时间；SolutionLimit 设定MIP可行解数量
• Tolerances 容差参数：控制求解器的最优或可行的偏差
  例如：MIPGap设置MIP的gap值，FeasibilityTol设置精度
• Simplex单纯形参数
  例如：InfUnbdInfo 控制是否获取不可行或无界模型的额外信息
• Barrier障碍法参数：控制障碍法
  例如：QCPDual 控制是否获取二次模型的对偶值
• Mip 混合整数参数：控制混合整数规划算法
  例如: BranchDir 设定优先分支方向；Heuristics 设定启发式算法求解时间所占的比重
• Mip Cuts 割平面参数：控制割平面
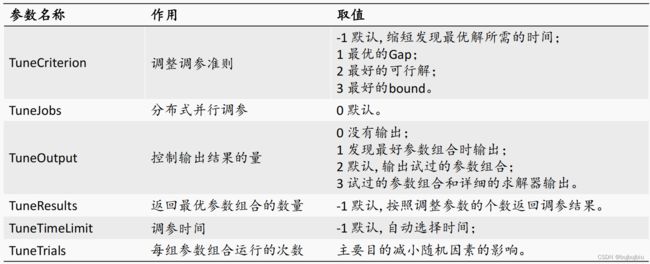
  例如: Cuts 设定割平面法的强度
• Tuning 调参参数：控制调参工具
  例如: TuneCriterion 设定调参的准则；TuneTimeLimit 设定调参的时间
• Multiple Solutions 多解参数：尝试寻找多个解
  例如: PoolSolutions 决定存储可行解的数量

还有一些其他参数Distributed algorithms 分布式计算参数；Compute Server 计算服务器参数；Cloud 云参数；Token server 令牌服务器参数；Other 其他一些参数

（3）参数设置方法

setParam(paramname,newvalue)

 - paramname 参数名称
 - newvalue 参数取值，可设定为'defult'

对于python，可以简写成model.Params.xxx，例如设置求解时间有如下写法

model.setParam('TimeLimit',600)
model.setParam(GRB.Param.TimeLimit,600)
model.Params.TimeLimit = 600

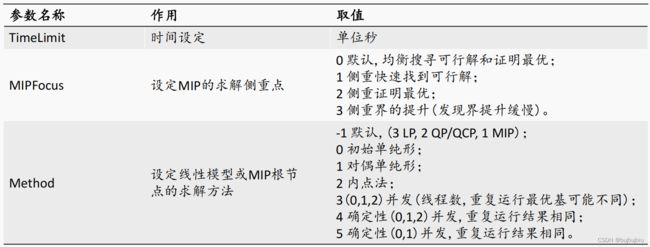
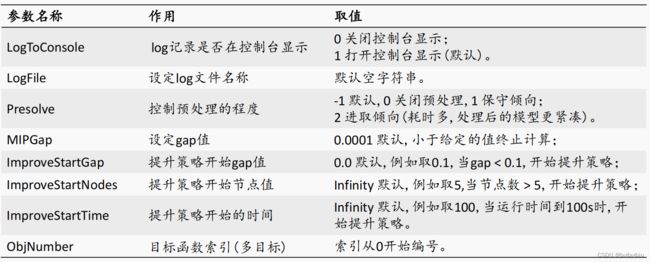
（4）常用参数

（5）参数使用案例

m.Params.TimeLimit = 2
m.Params.MIPFocus = i

import sys
import gurobipy as gp

if len(sys.argv) < 2:
    print('Usage: params.py filename')
    sys.exit(0)

# 读取模型验证是否为MIP问题
m = gp.read(sys.argv[1])
if m.IsMIP == 0:
    print('The model is not an integer program')
    sys.exit(1)

# 设定模型求解时间为2s
m.Params.TimeLimit = 2

# 用不同的MIPFocus值求解模型，选择有最小MIPGap值的模型
bestModel = m.copy()
bestModel.optimize()
for i in range(1, 4):
    m.reset()
    m.Params.MIPFocus = i
    m.optimize()
    if bestModel.MIPGap > m.MIPGap:
        bestModel, m = m, bestModel  # swap models

# 删除多余模型，重置求解时间
# 优化直到找到最优解
del m
bestModel.Params.TimeLimit = float('inf')
bestModel.optimize()
print('Solved with MIPFocus: %d' % bestModel.Params.MIPFocus)

（6）属性类别

• Model Attributes 模型属性
  例如：ModelSense 模型优化方向(最大化或最小化)；ObjVal 当前目标值
• Variable Attributes 变量属性
  例如：X 当前变量的取值； Start MIP初始解
• Linear Constraint Attributes 线性约束属性
  例如：Pi 约束对应的对偶值；Slack 约束的松弛量；RHS 约束的右端项
• Special-ordered Set constraints Attributes SOS约束属性
  例如：IISSOS 对不可行的模型，指示约束是否属于IIS (Irreducible Inconsistent Subsystem)
• Quadratic Constraint Attributes 二次约束属性
  例如：QCRHS 约束右端项
• General Constraint Attributes 广义约束属性
  例如：GenConstrName 约束名称
• Quality Attributes 解质量属性
  例如：BoundVio 最大的界违反； IntVio 整数变量离最近整数的最大距离
• Multi-objective Attributes 多目标属性
  例如：ObjN 对应多目标表达式中变量系数；ObjNVal 对应目标函数值

（7）属性设置和查询方法

属性设置，注意并不是所有的属性都可以设置

setAttr(attrname,newvalue)

 - attrname 属性名称
 - newvalue 属性值

var.setAttr(GRB.Attr.VType,'C'）
var.Vtype = 'C'

属性查询

getAttr(attrname,objs)

 - attrname 属性名称
 - objs（可选）列表或字典对象用来存储查询的值

model.getAttr(GRB.Attr.ObjVal)
model.GRB.Attr.ObjVa

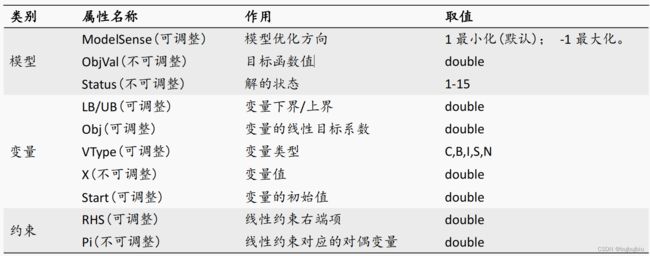
（8）常用属性

2. 自动参数调优

（1）调用自动调参工具

命令行
grbtune TuneTimeLimit=100 C:\gurobi801\win64\examples\data\misc07.mps

API
model.tune()

（2）调参参数

（3）调参案例

import gurobipy as gp
from gurobipy import *

# 设置模型
m = gp.Model("ooo")
x = m.addVars(3,4,vtype=GRB.BINARY,name='x')
m.addConstrs((x.sum(i,'*')<=1 for i in range(3)),name='con')
m.update()

# 返回最优参数组合的数量 = 1
m.Params.tuneResults = 1
# 设定调参时间
m.Params.tuneTimeLimit = 20
# 自动调参
m.tune()
# tuneResultCount 调参完成后存储的参数组合个数，其值<=tuneResult
# tuneResultCount > 0表明找到了最优参数组合
if m.tuneResultCount > 0:
    # 获得调参结果，索引0为最好
    m.getTuneResult(0)
    # 将调参结果写到prm格式文件中
    m.write('tune.prm')
    # 保存调参后的模型
    m.optimize()

3. 特殊约束的表达方式和使用

（1）广义约束

• Min：一组变量(包含常数)中取最小

addGenConstrMin(resvar,vars,constant,name)

 - resvar 变量 x = min(x1,x2,10)
 - vars 一组变量（可包含常数）
 - constant 常数
 - name 广义约束名称

例如：z = min(x, y, 3)

m.addGenConstrMin(z,[x,y],3,'minconstr')
m.addGenConstrMin(z,[x,y,3],name='minconstr')

# 换成一般的约束表达式
m.addConstr(z==min_([x,y,3]),'minconstr')
m.addConstr(z=min_(x,y,z),'minconstr')

• Abs：取绝对值

addGenConstrAbs(resvar,argvars,name)

 - resvar 变量
 - argvars 变量
 - name 广义约束名称

例如：x = |y|

m.addGenConstrAbs(x,y,'absconstr')

# 换成一般的约束表达式
m.addConstr(x==abs_(y),'absConstr')

• And：一组变量的值全等于1,则取1,否则取0。所有的变量都被视为0,1变量,不论他们之前被定为什么类型

addGenConstrAnd(resvar,vars,name)

 - resvar 变量
 - vars 一组变量
 - name 广义约束名称

例如：x = 1且y = 1，那么z = 1，否则 z = 0

m.addGenConstrAnd(z,[x,y],'andconstr')

# 一般约束表达式
m.addConstr(z==and_(x,y),'andconstr')

• Or：一组变量的值有一个等于1，则取1，否则取0。所有的变量都被视为0，1变量，不论他们之前被定为什么类型

addGenConstrOr(resvar,vars,name)

 - resvar 变量
 - vars 一组变量
 - name 广义约束名称

例如：x = 0且y = 0，那么z = 0，否则 z = 1

m.addGenConstrOr(z,[x,y],'orconstr')

# 一般约束表达式
m.addConstr(z==or_(x,y),'orconstr')

• Indicator：指示变量的值为1，约束成立，否则约束可以被违反

addGenConstrIndicator(binvar, binval, lhs, sense, rhs, name)

 - binvar 指示变量
 - binval 指示变量的值{0,1}
 - lhs 约束左端项
 - sense 约束符号
 - rhs 约束右端项
 - name 广义约束名称

例如：如果 z = 1，则 x+y <= 4

m.addGenConstrIndicator(z,True,x+y,GRB.LESS_EQUAL,4,'indictator')

# 一般约束表达式
m.addConstr((z==1)>>(x+y<=4))

（2）范围约束

addRange(expr,lower,upper,name)

 - expr 表达式
 - lower 下界
 - upper 上界
 - name 约束名称

例如： 5 <= x + y + z <= 10

m.addRange(x+y+z,5,10,'c')

# 一般约束表达式
m.addConstr(x+y+z=[5,12])

（3）SOS约束 Special-Ordered Set

SOS_TYPE1 表示一组有序变量中最多有一个变量取值不为0；
SOS_TYPE2 表示一组有序变量中最多有两个变量取值不为0,且非零变量相邻，变量是否相邻由权重决定；

addSOS(type,vars,wts=None)

 - type 约束种类(GRB.SOS_TYPE1 或者 GRB.SOS_TYPE2)
 - vars 变量
 - wts 变量对应的权重,且权重唯一,默认1, 2, 3.....

例如：

model.addSOS(GRB.SOS_TYPE2,[x,y,z],[1,2,4])

4. 特殊目标函数的表达方式和使用

（1）多个目标函数

所有的目标函数都为线性的,并且目标函数的优化方向一致(全部最大化或全部最小化)，可以通过乘以 -1 实现不同的优化方向。

setObjectiveN(expr,index,priority,weight,abstol,reltol,name)

 - expr 目标函数表达式
 - index 目标函数对应的序号（0，1，2....）
 - priority 优先级（整数值）
 - priority 权重（浮点数）
 - abstol 允许的目标函数值最大的降低量 abstol（浮点数）
 - reltol 允许的目标函数值最大的降低量reltol*|目标函数值|（浮点数）
 - name 目标函数名称

Gurobi 支持三种多目标模式：

• Blend（合成型）有权重，没有优先级，例如优化
  

m.setObjectiveN(x+y,0,weight=1,name='obj1')
m.setObjectiveN(x-5*y,1,weight=-2,name='obj2')

• Hierarchical（分层型）有优先级，例如优化
  

m.setObjectiveN(x+y,0,priority=10,name='obj1')
m.setObjectiveN(x-5*y,1,priority=5,name='obj2')

• 混合以上两种

m.setObjectiveN(x+y,0,weight=1,priority=10,name='obj1')
m.setObjectiveN(x-5*y,1,weight=-2,priority=5,name='obj2')

通过参数 ObjNumber 选择特定的目标,进而获得对应的目标函数值， ObjNumber 为多目标函数索引

for i in range(model.NumObj):
    model.setParam(GRB.Param.ObjNumber,i)
    print(f'obj {i} = {model.ObjNVal}')

（2）分段线性函数

对一些非线性模型，可以使用这一功能去线性逼近

setPWLObj(var,x,y)

 - var 指定变量的目标函数是分段线性
 - x 定义分段线性目标函数的点的横坐标（非减序列）
 - y 定义分段线性目标函数的点的纵坐标

例如：

m.setPWLObj(x,[0,2,5],[0,2,3])
m.setAtrr(GRB.Attr.ModelSense,-1)

5. Solution Pool 的使用

Gurobi在搜寻最优解的过程中,会找到一些次优解(sub-optimal solutions)，有时候用户也希望知道次优解的具体情况。因此Gurobi会将计算过程中发现的所有解记录在Solution Pool里供用户查询。Solution Pool参数如下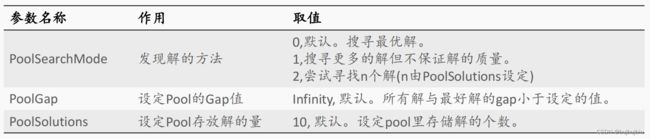
Solution Pool 里的解按照质量非增排序,并从零开始编号。因此查询具体解的情况(变量值和对应目标值等)，需要先设定参数SolutionNumber 的值，然后通过模型属性PoolObjVal 和变量属性Xn 获得目标值和变量值。
例如：查找pool里面第4个解（索引=3）的目标值和变量值

model.setParam(GRB.Param.SolutionNumber,3)
print(model.PoolObjVal)
for i in range(model.NumVars):
    print(f'var {Vars[i].Varname};value {Vars[i].Xn}')

更多python+gurobi的使用案例见Gurobi官网Build Your Optimization Skills with Python