Discrete Optimization课程笔记(2)—约束规划（上）

目录

1.约束规划（Constraint Programming）

2.约束传播（constraint propagation）

Case1: Send More Money

3.元素约束（Element constraint）

Case2: Magic Series

Case3: Stable Marriages

4. 全局约束（Global Constraints）

Case4: 8位皇后

Case5: 九宫格

 5. 对称性破缺（symmetry breaking）

Case6: Balanced Incomplete Block Designs (BIBDs)

Case7: Scene Allocation

---

1.约束规划（Constraint Programming）

（1）约束规划

• 使用约束减少每个变量取值集合
• 移除不可能出现在任何解的值
• 精确解而非启发式解：足够时间，能找到满意解和最优解
• 重点：怎么使用约束缩小搜索空间，排除不可能出现在任何解的取值

（2）经典问题

• 8个皇后：将8个棋子摆放在8*8的棋盘上，要求每两个棋子不能在相同行，列以及对角线
• 地图着色：给一张地图上色，要求相邻国家不能颜色相同

四色定理：任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色 

（3）约束（constraint ）的作用

• 检查在变量域里是否存在可行解（Feasibility checking）
• 如果有可行解，约束能决定变量域中的某些值是否是可行解（Pruning）

域（domain）：一个变量的域即为其可能取值的集合，D(x)={1,2,3} 

2.约束传播（constraint propagation）

（1）约束传播过程

Case1: Send More Money

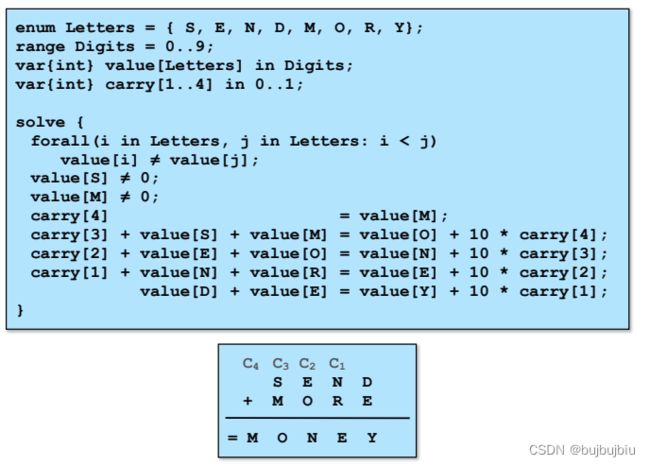
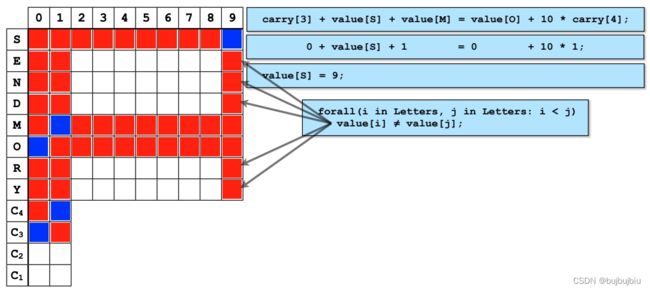
以Send More Money为例说明constraint propagation过程，按照下面的公式找到每个字母对应的数字，引入4个辅助变量代表进位。模型如下，字母取值0-9，进位取值0-1，每个字母代表不同的数字，S和M是首位，不能为0，每列有计算等式

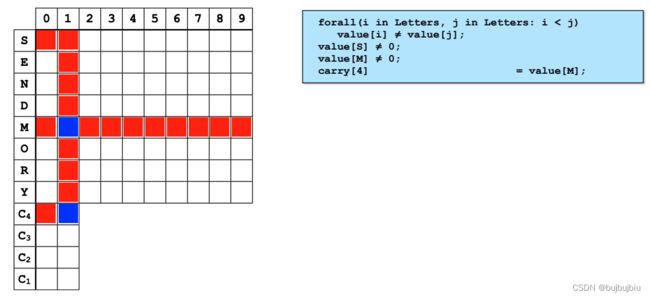
 （1）前四个约束：左图为搜索空间，根据前四个约束得出value[M]=carry[4]=1

 （2）约束5：carry[3] + value[S] + value[M] = value[O] + 10 * carry[4]

• carry[3]为0～1，value[S]为2～9，value[M]=1，左边等式为3～12
• carry[4]=1，value[O]为0和2～9，右边等式10~19
• 取左右两边交集为[10,11]
• 10 <= carry[3] + value[S] + 1 <= 11，因此8 <= value[S] <= 10
• 10 <= value[O] + 10 * carry[4] <= 11，因此0 <= value[O] <= 1，即value[O]=0
• 更新搜索空间，字母取值不能相通

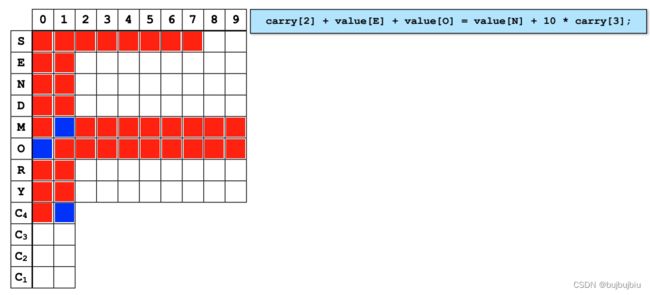
 （3）约束6：carry[2] + value[E] + value[O] = value[N] + 10 * carry[3]

• value[O] = 0，0 <= carry[2] <= 1，2 <= value[E] <= 9，2 <= 左边 <= 10
• 2 <= value[N] + 10 * carry[3] <= 10，因此-7 <= 10 * carry[3] <= 8，即carry[3] = 0

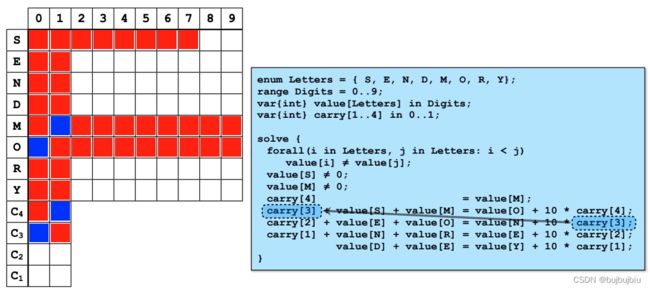
 （4）回溯到约束5：carry[3] + value[S] + value[M] = value[O] + 10 * carry[4]

•  carry[3] = 0，value[M] = carry[4] = 1，value[O] = 0，因此value[S] = 9
• 后面的约束条件得出的值可以再作用到前面的约束，再次缩小搜索空间 

（2）通用形式

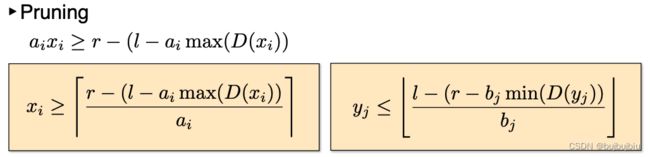
 对于整数线性约束，有以下通用形式

3.元素约束（Element constraint）

用包含变量的表达式索引一个数组或者矩阵

Case2: Magic Series

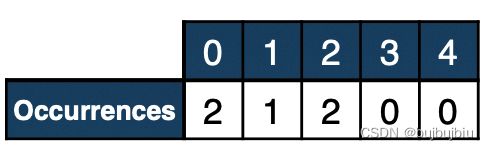
如果在一个序列 S=(S0,S1,S2...Sn) 中，S(i)代表i在S中出现的次数，那么S称为Magic Series。如下为一个Magic Series，S[0]=2，表示0出现了两次。

Reification：将约束变成0/1变量，如果约束成立，变量取值为1，否则取值为0。对每一个k，引入0/1变量b[i]，如果series[i] = k，那么b[i] = 1，否则b[i] = 0，series[k]为b的所有值和。

Case3: Stable Marriages

假设有四个男生分别是George,Hugh,Will,Clive，四个女生分别是Julia,Halle,Angelina,Keira，每个女生（男生）都对所有男生（女生）有一个偏好等级。例如对于Halle，男生的排名分别为Clive,George,Will,Hugh；对于Hugh，女生的排名分别为Angelina,Halle,Clive,George。什么情况下婚姻是稳定的？以Hugh和Angelina为例，如果Angelina喜欢George多过Hugh，那么George一定要喜欢他配偶多过Angelina，如果Hugh喜欢Julia多余Angelina，那Julia一定要喜欢他配偶多过Hugh，满足上述两个条件的婚姻才是稳定的。建模如下

• wrank[Men,Women] 代表对于Men来说，Women的排序；mrank[Women,Men] 代表对于Women来说，Men的排序
• 决策变量：wife[Men]代表Men的妻子，husband[Women]代表Women的丈夫
• 约束条件（一致）：对于每一个男人，他的妻子对应的丈夫是他自己，即 husband[wife[m]] = m；同样对于每一个女人，他的丈夫对应的妻子是她自己，即 wife[husband[w]] = w
• 约束条件（稳定）：对于每一个m，如果m比起他的妻子更喜欢w（wrank[m,w] < wrank[w,wife[m]]），那么对于w，她要比起m更喜欢她的丈夫（mrank[w,husband[w]] < mrank[w,m]）。对于每一个w，也是同理。

4. 全局约束（Global Constraints）

全局约束是捕获非固定数量的变量之间的关系的约束

Case4: 8位皇后

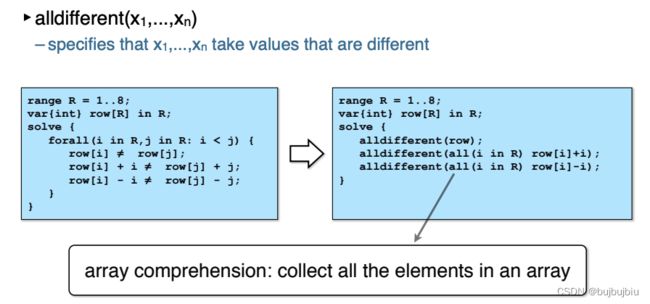
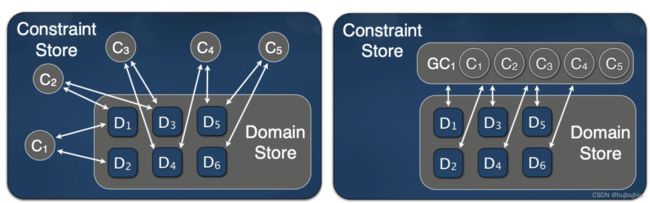
 例如要求所有变量取值不同，可以用全局约束alldifferent表示。在8个皇后问题问题，原始模型如下图左，每列放一个值1，行不确定，所有元素的行不同row[i] ≠ row[j]，上对角线不能相同row[i] + i ≠ row[j] + j，下对角线不能相同row[i] - i ≠ row[j] - j。转化成全局约束如下图右，用一个alldifferent可表示原先的三个约束。

 （1）那为什么需要全局约束？ 

• 全局约束能更快检测是否有可行解

 从全局约束角度：要求x1，x2，x3不能相同，域中只有1，2取值，因此无可行解。从元素约束角度：包含三个约束x1 ≠ x2, x2 ≠ x3, x3 ≠ x1，对每一个约束都能找到满意的解，因此会判断有可行解。即一个全局约束和3个元素约束表达意思相同，但是最终结果不同，在约束规划中约束的设置非常重要。

•  全局约束使得可以更多地修剪搜索空间

 从全局约束角度：可得x3 ≠ 2。从元素约束角度：对每一个约束，并不能缩小搜索空间。

Case5: 九宫格

九宫格模型如下：第一个约束代表每行不重复，第二个约束代表每列不重复，第三个约束代表3*3的方框元素不重复。

 根据约束条件可以选出第一个确定的位置放2（不重复性），最终只有个两个位置是任意选择就能完成整个九宫格。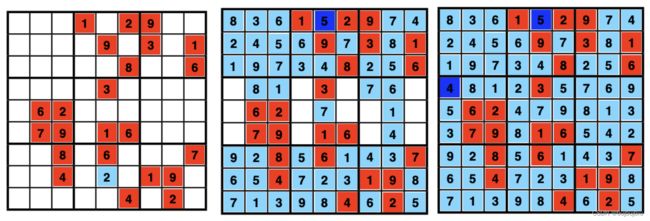

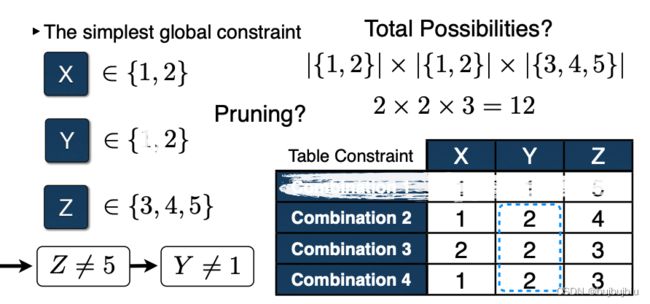
（2）最简单的全局约束（表格约束） 

 5. 对称性破缺（symmetry breaking）

许多问题都表现出对称性，搜索解空间的对称部分是无用的，对称性包括值对称和变量对称，使用对称性破缺可以解决该问题

Case6: Balanced Incomplete Block Designs (BIBDs)

平衡不完全区组设计(BIBDs)

• 输入：（v,b,r,k,l）
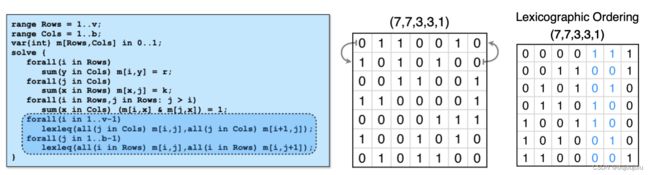
• 输出：v行b列的0/1矩阵，矩阵每行有r个1，每列有k个1，矩阵内积为l，即任意两行向量内积值为l

如下图为BIBDs矩阵，7*7矩阵，每行3个1，每列3个1，每两行内积为1，BIBDs矩阵是不唯一的，因此交换任意两行或者两列，都满足条件，即有很多解。为此引入词典排序（Lexicographic ordering），a = 0 1 1 0 0 1 0，b = 1 0 1 0 1 0 0，则a <= b，反之如果a = 1 1 1 0 0 1 0，则a >= b。调整所有行和所有列得到右图。

Case7: Scene Allocation

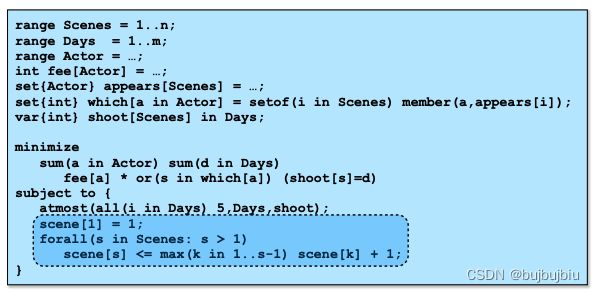
有一群演员Actor，一系列场景Scenes，拍摄天Days，fee[Actor]代表每个演员每天拍摄的费用，每个场景需要一些演员，每天最多拍摄k个场景。目的是安排每个场景在第几天拍摄能最小化总成本。下面模型中shoot[Scenes]代表决策变量，appears[Scenes]表示每个场景需要出现的演员，which[a in Actor] = setof(i in Scenes) member(a,appears[i])计算了每位演员需要参与的场景。目标函数fee[a] * or(s in which[a]) (shoot[s]=d)计算所有演员的拍摄费用。约束条件atmost(all(i in Days) 5,Days,shoot)限制每天最多拍摄k个场景。

该问题中的对称性在于：把第一天的所有场景和第二天的所有场景交换，解的目标值是一样的，也就是说，天和天没有区别。为了消除值的对称性，可以假设场景1只能安排在第一天，场景2可以安排在1，2天，以这样的规律每个场景只考虑已经使用过的天加上新一天。