【西瓜书+南瓜书】学习笔记3
决策树是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果。如下图所示:

划分选择
决策树如何选择最优划分属性?一般而言,随着划分过程不断进行,我们希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的"纯度" (purity) 越来越高。
基于信息增益(information gain)的ID3决策树
- 信息熵(information gain)
衡量样本纯度的一个指标,信息熵越小,则纯度越高,并且信息熵也是度量随机变量不确定性的指标,信息熵越大,随机变量越不确定。其公式定义如下:
E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k log 2 p k Ent(D)=-\sum\limits_{k=1}^{\mid y \mid}p_{k}\log_{2}{p_{k}} Ent(D)=−k=1∑∣y∣pklog2pk
其中, p k p_{k} pk为第 k k k类样本的概率, ∣ y ∣ \mid y \mid ∣y∣表示类别的个数,实际上,信息熵是自信息的期望。 - 条件熵
Y的信息熵关于概率分布X的期望 H ( Y ∣ X ) = ∑ x p ( x ) H ( Y ∣ X = x ) H(Y\mid X)=\sum\limits_xp(x) H(Y\mid X=x) H(Y∣X)=x∑p(x)H(Y∣X=x) - 信息增益
信息增益=信息熵-条件熵
信息增益越大,则意味着使用该属性来进行划分所获得的纯度提升越大,ID3决策树学习算法就是以信息增益为准则来划分属性。
基于增益率的C4.5决策树
基于信息增益(information gain)的ID3决策树存在一个缺陷,就是对可取值数目较多的属性有所偏好。例如一个属性具有17个取值,每个取值包含一个样本,则划分的节点仅包括一个样本,显然此时纯度最大,但是这样划分会使模型缺乏泛化能力。因此使用增益率来选择最优划分属性。增益率定义为:
信息增益 = 增益率 / 属性 a 的固有值 信息增益=增益率/属性a的固有值 信息增益=增益率/属性a的固有值
属性a的固有值定义为:
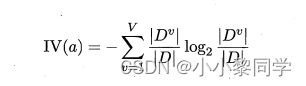
当属性a可取值较多时,属性a的固有值通常会较大
注意:增益率准则对可取值数目较少的属性有所偏好,因此 C4.5 算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式算法。
启发式算法: 找出信息增益高于平均水平的属性,然后从中,筛掉属性可取值多的属性,即选择增益率高的。
基于基尼指数的CART决策树
CART决策树是Classification And Regression Tree的简称,分类和回归树,顾名思义可用于分类和回归任务中。CART决策树是使用基尼指数最小的属性作为最优划分属性。数据集中可用基尼值来度量纯度,基尼值公式定义如下:

基尼值反映了从数据集中随机抽取两个样本,其类别标记不一致的概率.因此, 基尼值越小,则数据集的纯度越高
基尼指数

需要注意的是,实际情况中,通常把属性值的取值分为两部分进行算基尼指数,最后在选择最小的基尼指数所对应的属性及范围确定为最优划分属性点。
使用基尼指数和熵的鸢尾花数据分类案例
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
接下来定义加载鸢尾花数据函数,需要注意的是这里使用了分词抽样,因为官网提供的标签数据中,前50个样本为类别0,中间50个样本为类别1,后面50个样本为类别2。
def test_DecisionTreeClassifier(*data):
X_train,X_test,Y_train,Y_test=data
clf=DecisionTreeClassifier()
clf.fit(X_train,Y_train)
print("训练得分:%f"%(clf.score(X_train,Y_train)))
print("测试得分:%f"%(clf.score(X_test,Y_test)))
X_train,X_test,Y_train,Y_test=load_data()
test_DecisionTreeClassifier(X_train,X_test,Y_train,Y_test)
运行结果:

DecisionTreeClassifier函数默认使用基尼指数评分准则,接下来考察不同的平均准则criterion对应分类性能的影响。
def test_DecisionTreeClassifier_criterion(*data):
X_train,X_test,Y_train,Y_test=data
criterions=['gini','entropy']
for criterion in criterions:
clf=DecisionTreeClassifier(criterion=criterion)
clf.fit(X_train,Y_train)
print("评分准则:%s"%criterion)
print("训练得分:%f"%(clf.score(X_train,Y_train)))
print("测试得分:%f"%(clf.score(X_test,Y_test)))
X_train,X_test,Y_train,Y_test=load_data()
test_DecisionTreeClassifier_criterion(X_train,X_test,Y_train,Y_test)
