Python--Numpy基础
Numpy是Python的一个能快速处理矩阵运算的数学库,如果你从事的是数据科学,或者机器学习领域的话,Numpy是一项最基本的技能。他不仅简化了我们在处理矩阵运算时需要编写的代码,而且,许多Numpy的底层函数用C编写,我们能获得在用普通Python自带的列表结构时,所无法达到的运算速度。
下面,我将就Numpy的一些基本用法,做个简单的介绍,当然,一来Numpy库本身会不断更新,二来,我本人的认知也会随时间改变,所以,这部分内容也会随时更新。当然一些我认为不太常用的方法、结构,不会出现在本文中,使得本文尽量简洁明了。
因为Numpy并不是Python本身自带的库,所以,使用之前,当然需要先安装,具体的方法,百度一下会有很多,我在此就略了。所以,我默认所有对这部分内容感兴趣的人都已经安装好了Numpy,并且有一定的Python语言基础。需要注意的是,为了使得文中的代码尽量简洁,所有出现的代码都默认已经引入了Numpy库,并简写为np。也就是说,所有代码都默认在它们之前导入了numpy库:import numpy as np
创建数组
1. np.array() 函数创建数组
Numpy为我们提供的创建数组的方法可以说非常丰富,针对某些特殊类型的数组还有专门的函数,但是基本上讲,有以下三种:
(1) Numpy中的数组类型——ndarray
a = np.array([1, 2, 3]) # >>> [1 2 3]
b = np.array((1, 2, 3.5)) # >>> [1. 2. 3.5]
print(type(a), type(b)) # >>> <class 'numpy.ndarray'> <class 'numpy.ndarray'>我们将一个序列传递给np.array() 函数(其实,这个序列不一定是列表,元组,甚至字符串都可以),会生成一个新的 ndarray 型的对象,这就是Numpy中的数组了,从形式上中也可以看出,这种对象不同于列表,中间是没有 “,” 分隔的。
我们发现,当传入的序列中的元素是不同类型时,生成ndarray对象后,元素的类型会受到影响,比如,上面的例子中,当整型和浮点型都存在时,生成的对象中原本是整型的元素也变成了一种特殊的浮点型(这种类型时ndarray对象所特有的),考虑到一般只是进行数学意义上的运算,所以尽量避免在传入的序列中加入字符串这种操作,以免类型错乱,造成不必要的麻烦。
当然,np.array()函数也适用于生成多维数组。
m = np.array([[1, 2], [3, 4]]) # >>> [[1 2]
[3 4]]需要注意的是,想要用序列生成数组,传入函数的一定是一个完整的序列,而不能只是元素的排布
a = np.array(1, 2, 3) # >>> 错误!
a = np.array([1, 2, 3]) # >>> 正确!其实,在实际应用中,一般我们就把Numpy中的多维数组当做矩阵,来执行相关运算。所以,正确地创立数组,是开始所有代数运算的先决条件。
(2) ndarray型对象的属性
此外,和其他数据类型一样,我们可以查看”ndarray”型对象的相关属性:
ndarray.dtype:数据类型
a = np.array([1.5, 2, 3], dtype=int) #设置数组中元素的数据类型为整型
print(a) # >>> [1 2 3]
b = np.array([[1, 2.3], [4.1, 5.0]])
print(b.dtype) # >>> float64,访问数组b的数据类型ndarray.shape:数组大小
a = np.array([1, 2, 3])
b = np.array([[1], [2], [3]])
print(a.shape) # >>> (3,)
print(b.shape) # >>> (3, 1) # shape实际上是一个元组也可以通过设置shape来改变数组的形状:
a = np.array([1, 2, 3, 4], [4, 2, 3, 1], [3, 4, 2, 1]) # 现在,a是3 x 4的矩阵
a.shape = 4, 3 # a的形状被改变
print(a) # >>> [[1 2 3]
[4 4 2]
[3 1 3]
[4 2 1]]ndarray.ndim:数组的维度
a = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]], [[9, 10], [11, 12]]])
b = np.array([[1], [2], [3]])
print(a.ndim) # >>> 3
print(b.ndim) # >>> 2ndarray.size:数组中元素的总个数
a = np.array([1, 2, 3])
b = np.array([[1], [2], [3]])
print(a.size) # >>> 3
print(b.size) # >>> 3当然,ndarray对象还有很多其他属性,这些属性有助于我们更好地控制数组对象,基本使用方法与上面类似,不再赘述。
2. 创建数组过程中常用的其他函数
需要注意的一点是:上面的例子都是先创建一个Python序列,然后通过array()函数将其转换为数组,这样做显然效率不高。因此NumPy提供了很多专门用来创建数组的函数。以方便用户在已知数组是具备的某种特殊性质下,快速创建数组。
(1)np.arange()依据范围特征创建数组
之前,我们知道Python基本语法里的 range() 函数可以根据数值范围生成列表,同样的,我们在Numpy中通过 arange() 函数,按照一定规律生成数组。
a = np.arange(5) # >>> [0 1 2 3 4]
b = np.arange(1, 7, 2) # >>> [1 3 5]语法上讲,和 range() 函数是一致的,都是由三个参数 `(start, stop, step)组成
(2)np.linspace()
作用与arange()类似,三个必要的参数:”start, stop, num”,不过默认状态下包含终值。
a = np.arange(1, 7, 3) # >>> [1. 4. 7.](3)np.logspace()
函数和linspace类似,不过它创建等比数列,参数设置为:(start, stop, num=50, endpoint=True, base=10.0, dtype=None),一般我们只设置”start, stop, num”3个参数,表示等比数列的起始点是 basestart ,终止点为 basestop 。当然,有时候也需要改变base值。比如产生 20 到 24 之间的5个数构成数组:
a = np.logspace(0, 4, 5, base=2) # >>>[1. 2. 4. 8. 16.](4)np.fromfunction()
fromstring, frombuffer, fromfile, fromfunction这些函数从其他对象中抽取序列,构建数组。其中,我个人认为比较有用的是fromfunction,其参数设置为np.fromfunction(function, shape),由一个函数和数组形状作为输入。需要注意的是,数组中每个位置的值为这个位置的坐标输入function的计算结果,当然,函数有 n 个参数时,就只能生成n维数组了
# 定义函数,这里的函数只有1个参数
def foo1(i):
return i % 2
# 注意fromfunction()中,第2个参数shape的输入形式是元组
a = np.fromfunction(foo1, (2,)) # >>> [ 0. 2.]
b = np.fromfunction(lambda x, y: x + y, (2, 3)) # >>> [[ 0. 1. 2.]
[ 1. 2. 3.]](5)np.zeros(),np.ones(),np.eye()等方法可以构造特定的矩阵
上面这3个函数分别用来构造零矩阵;元素全为1的矩阵,以及单位矩阵(主对角线为1,其余元素为0)。他们的作用是帮助我们对这些特殊的矩阵实现快速构造。
# 参数为数组形状
a = np.zeros((2, 3)) # >>> [[ 0. 0. 0.]
[ 0. 0. 0.]]
b = np.ones((2, 3)) # >>> [[ 1. 1. 1.]
[ 1. 1. 1.]]
# 参数为方阵的行数(列数)
c = np.eye(3) # >>> [[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]3. 给矩阵添加行或列
有时,需要我们在已有的矩阵中,添加一行,或者一列。这里主要介绍2种实现方法。
(1)np.r_[]和np.c_[]分别添加行和列,生成新的矩阵:
如下代码所示,现在要在矩阵a中添加一行
a1 = np.array([[1, 2, 3], [4, 5, 6]])
b1 = np.array([[0, 0, 0]])
print(np.r_[a1, b1]) # >>>[[1 2 3]
[4 5 6]
[0 0 0]]注意此时b1的写法,也是一个二维矩阵,且列数与a相等。再比如,添加一列:
a1 = np.array([[1, 2], [3, 4], [5, 6]])
b1 = np.array([[0], [0], [0]])
print(np.c_[a1, b1]) # >>>[[1 2 0]
[3 4 0]
[5 6 0]]同样,需要注意此时b1的写法。
(2)np.row_stack()和np.column_stack()分别添加行和列,生成新的矩阵:
还有两个与np.r_[]和np.c_[]类似的函数:np.row_stack()和np.column_stack()。但是它们的用法更加自由,所添加的行或列,要求只要是序列(也就是说列表,元组皆可)就行,不需要像np.r_[]和np.c_[]那样严格要求添加的东西必须是数组了。具体用法网上容易查到,此处省略。
此外,还有一些别的创建数组的方法,限于篇幅,不再介绍了,若遗漏了重要的方法,会随时补充。
访问数组
1. 切片
与列表的性质类似,通过切片的形式,可以访问已经构建好的数组。
比如对于一维数组:
a = np.arange(5) # >>> [0 1 2 3 4]
print(a[2:3]) # >>> [2]
print(a[::2]) # >>> [0 2 4]语法规则与列表中的切片一致,包含起始点,且不包含终止点。需要注意的是,这种数组切片返回的是原始数组的一个视图,与原始数组共享相同的内存空间,而并没有建立新的数组。
a = np.arange(5) # >>> [0 1 2 3 4]
print(id(a[2])) # >>> 4366848312
print(id(a[2:3][0])) # >>> 43668483122. 访问矩阵的行与列
在切片的方法中,我要特别强调一个细节,就是对矩阵行、列的访问。因为这个知识点经常用到,所以特地列一小节出来。但是基本方法就是切片了。
- 访问矩阵的行
a = np.array([[1, 2, 3], [4, 5, 6]])
# 访问矩阵第0行
print(a[0]) # >>> [1 2 3]
# 访问矩阵第0行的0,1两列
print(a[0][:2]) # >>> [1 2]- 访问矩阵的列
a = np.array([[1, 2, 3], [4, 5, 6]])
# 取矩阵a第2列
print(a[:, 2]) # >>> [3 6]当然,这是取全列,你也可以根据切片控制某一列中,行的范围,具体做法跟上面的取一行时一致。
3. for循环遍历矩阵
如果要遍历整个矩阵,for循环是非常合适的选择。
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# for循环遍历行
for row in a:
print(row) # >>> [1 2 3]
# >>> [4 5 6]
# >>> [7 8 9]
# for循环遍历列
for col in np.transpose(a):
print(col) # >>> [1 4 7]
# >>> [2 5 8]
# >>> [3 6 9]np.transpose()是计算矩阵转置的函数,这个后面会说。
4. 使用整数序列访问
其实最简单的访问数组单个元素的做法是通过元素的下标(包括多维数组也是一样)。这一点我在上面虽然没有强调,但是早开始这么用了。但是当现在的任务变成访问数组中个别几个位置的元素,而这些位置又是毫无规律的(不太方便使用切片),那也可以方便地使用整数序列作为下标解决这个问题。
a = np.arange(0, 20, 2) # >>> [ 0 2 4 6 8 10 12 14 16 18]
# 直接通过数组`np.array([1, 4, 5, 7])`,访问1, 4, 5, 7位的元素
print(a[np.array([1, 4, 5, 7])]) # >>> [ 2 8 10 14]也可以通过列表建立要访问的下标序列,但是需要先通过一个名称引用这个列表
b = np.array([[1, 2, 3], [4, 5, 6]]) # 二维数组
# 访问第一行的第0列,第1列;访问第2行的第1列,第2列
index = [[0, 1], [1, 2]]
print(b[index]) # >>> [2 6]然而需要注意一下,这里不能用ndarray型对象的引用作为下标,因为解释器会认为应该在数组的第一行取值
b = np.array([[1, 2, 3], [4, 5, 6]])
index1 = np.array([[0, 1], [1, 2]])
index2 = np.array([[0, 1], [1, 0]])
index3 = [[0, 1], [1, 0]]
print(b[index1]) # >>> wrong!因为范围超了,index1中的元素2会让解释器寻找b的第2行,找不到
print(b[index2]) # >>> [[[1 2 3]
[4 5 6]]
[[4 5 6]
[1 2 3]]]
print(index3) # >>> [2 4],第0行第1列,以及第1行,第0列上面的东西看上去“规矩”很多,其实用的时候最好直接引用建立好的列表就行,这样最方便。再者,就是临时写个小脚本试一下,最稳妥。
5. 通过布尔数组访问
这是一种非常特殊的方法,举个例子来说,如下:
a = np.arange(12).reshape(3, 4) # 建立了一个3 x 4的矩阵
# b是一个布尔数组,这个布尔数组与a形状相同,其中每个元素表示a中对应位置的元素是否比4大
b = a > 4 # >>> b = [[False False False False]
[False True True True]
[ True True True True]]
print(a[b]) # >>> [ 5 6 7 8 9 10 11]也可以通过布尔数组来选择一个数组的行和列
a = np.arange(12).reshape(3, 4)
b1 = np.array([False, True, True])
b2 = np.array([False, True, True, False])
# 按bool属性取行
print(a[b1,:]) # >>> [[ 4 5 6 7]
[ 8 9 10 11]]
# 按bool属性取列
print(a[,:b2]) # >>> [[ 1 2]
[ 5 6]
[ 9 10]]线性代数运算
这是Numpy最吸引人的地方了。我们常见的矩阵、向量的运算基本在Numpy中都能找到现成的函数,为快速开发提供了可能。操作中,”ndarray”型对象既然可以表示多维数组,那么当然也可以表示我们最常用的矩阵。实际上,Numpy中,我们对矩阵操作时,用”ndarray”型对象的频率甚至高过了标准的矩阵对象”np.matrix()”.
1. 矩阵转置
ndarray.transpose()函数直接生成转置矩阵
a = np.array([[1, 2],[3, 4]])
print(a.transpose()) # [[1 3]
[2 4]]2. 矩阵的迹
np.trace()函数输出矩阵的迹,即方阵主对角线上元素之和。若所要计算迹的矩阵非方阵,则计算行列序相等的元素之和。
a = np.array([[1, 2],[3, 4]])
b = np.array([[1, 2, 3],[4, 5, 6]])
print(np.trace(a)) # >>> 5
print(np.trace(b)) # >>> 6(由1 + 5生成的)3. 矩阵乘法
np.dot(a, b)表示两个矩阵之间的乘法,在Python3中,一个更简单的符号@表示矩阵之间的乘运算。注意:符号*不能表示ndarray对象之间相乘。
a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[1, 2], [3, 4], [5, 6]])
print(np.dot(a, b)) # >>> [[22 28]
[49 64]]
print(np.transpose(b) @ np.transpose(a)) # >>> [[22 49]
[28 64]]4. 矩阵的加减、数乘
+, -, *, /这些运算符能直接执行矩阵的基本运算,当然,都是按元素进行的。其中乘法特指数乘,跟我们用的最多的矩阵乘法不同。
a = np.array([[1, 2, 3],[4, 5, 6]])
b = np.array([[6, 5, 4],[3, 2, 1]])
# 矩阵对应元素做加减
print(a + b) # >>> [[7 7 7]
[7 7 7]]
print(a - b) # >>> [[-5 -3 -1]
[ 1 3 5]]
# 矩阵所有元素与某数相乘
print(a * 2) # >>> [[ 2 4 6]
[ 8 10 12]]
# 矩阵所有元素的次幂
print(a ** 2) # >>> [[ 1 4 9]
[16 25 36]]5. 随机矩阵
子库random用于生成随机的数组、矩阵等等。这里我简略举2个例子,用法跟标准库中的random模块类似,具体可以查阅相关文档。
np.random.rand(a, b)函数用来生成a行b列的矩阵,矩阵中每个元素都是随机的浮点数,范围在 [0,1) 。
a = np.random.rand(2, 3) # >>> [[ 0.23600569 0.62347282 0.84519854]
[ 0.85702323 0.10537731 0.59344112]]np.random.randint(low, high, size)函数用来生成形状为size的随机矩阵,其中,矩阵的每一个元素都是整数,且范围在 [low,high) 之间。
a = np.random.randint.rand(0, 10, (2, 3)) # >>> [[7 0 9]
[5 4 7]]5. 矩阵的逆与计算行列式
Numpy的线性代数子库linalg也是需要了解一下的,它有两个特别重要的应用:求取矩阵的逆;计算行列式
- 矩阵求逆:
np.linalg.inv(ndarray)
a = np.random.randint(0, 10, (3, 3)) # >>> [[7 1 5]
[7 8 1]
[0 3 0]]
print(np.linalg.inv(a)) # >>> [[-0.03571429 0.17857143 -0.46428571]
[ 0. 0. 0.33333333]
[ 0.25 -0.25 0.58333333]]- 计算行列式:
np.linalg.det(ndarray)
a = np.random.randint(0, 10, (3, 3)) # >>> [[2 6 3]
[8 5 4]
[2 8 0]]
print(np.linalg.det(a)) # >>> 1466. 向量的最大最小值、加和、平均值、范数
实现这些对向量的运算代码如下:
a = np.random.randint(0, 10, (1,)) # >>> [6 5 1 4 5 9 8 9 0 0]
print(np.sum(a)) # >>> 47
print(np.max(a)) # >>> 9
print(np.min(a)) # >>> 0
print(np.average(a)) # >>> 4.7
print(np.linalg.norm(a)) # >>> 18.1383571472其实,最后一项范数的计算,我们当然可以令这个向量与自身做内积,再开根号。当然,上面代码中的写法却是更加简洁方便。
有些时候我们想要一次性求得矩阵每一行或者每一列的最大最小值,加和,平均值等等,这个时候,“轴”参数的设置就显现出作用了。
a = np.random.randint(0, 10, (3, 3)) # >>> [[3 7 1]
[1 0 3]
[3 6 2]]
print(np.sum(a, axis=0)) # >>> [ 7 13 6]
print(np.sum(a, axis=1)) # >>> [11 4 11]
# 如果直接求sum,得到的会是全部元素的加和
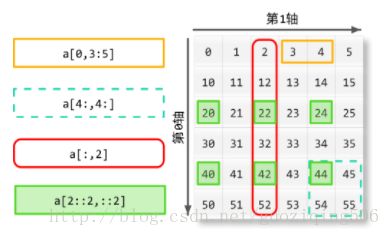
print(np.sum(a)) # >>> 26轴(axis)的含义其实表示的是矩阵的维度,比如拿一个二维矩阵来说,其轴的表示如下图:
上图来源:python中的sum函数.sum(axis=1). 这个图其实也把上面所说的切片的内容形象地表述了。
8. 向量内积
其实,这个东西可以用矩阵乘法解决,但是对于一维数组来说,还有个专门的函数np.inner(v1, v2),因为我在工作中经常会用到这种一维数组计算内积的情况,故在此列出:
v1 = np.array([1, 2, 3])
v2 = np.array([2, 3, 4])
print(np.inner(v1, v2)) # >>> 20关于Numpy基础知识,我暂时想到的就是以上这些了。因为Numpy的内容实在太多,所以我写的一定不全。还希望读者们有什么好的提议尽可提出,我再添加。这篇博客将在未来,不定时更新。