Kruskal算法
同样是求最小生成树,kruskal适合从边的角度出发,因此适合稀疏图。而prim算法从点的角度出发,适合稠密图。
时间复杂度为O(eloge)。因为外层循环了e(边数)层,而内部find循环了loge层。
算法首先把二维矩阵图转化为边图
for(i=0;i<MAXSIZE;i++){ for(j=0;j<MAXSIZE;j++){ flag = 1; if(i != j && num[i][j] != INF){ for(k=0;k<=max;k++){ if(g->e[k].begin == j && g->e[k].end == i){ flag = 0; break; } } if( flag ){ g->e[max].begin = i; g->e[max].end = j; g->e[max].length = num[i][j]; //printf("[%d]%d %d %d \n",max,g->e[max].begin,g->e[max].end,g->e[max].length); max++; } } } }
通过冒泡排序,排序边数组
void bubblesort(Graph *g,int len){ int i,j; for(i=0; i < len; i++){ for(j = len-1; j>i; j--){ if(g->e[j].length < g->e[i].length){ swap(g,i,j); } } } } void swap(Graph *g,int i,int j){ edge *pool = (edge *)malloc(sizeof(edge)); pool->begin = g->e[j].begin; pool->end = g->e[j].end; pool->length = g->e[j].length; g->e[j].begin = g->e[i].begin; g->e[j].end = g->e[i].end; g->e[j].length = g->e[i].length; g->e[i].begin = pool->begin; g->e[i].end = pool->end; g->e[i].length = pool->length; free(pool); }
最后通过kruskal,从最小便开始,连接图。
for(i=0;i<max;i++){ n = find(parent,g->e[i].begin); m = find(parent,g->e[i].end); if(n != m){ parent[n] = m; printf("[%d %d] %d \n",g->e[i].begin,g->e[i].end,g->e[i].length); } }
全部代码

#include <stdio.h> #include <string.h> #include <stdlib.h> #define MAXSIZE 9 #define INF 65535 typedef struct edge{ int begin; int end; int length; }edge; typedef struct Graph{ edge e[20]; }Graph; int num[MAXSIZE][MAXSIZE]={ 0, 10, INF,INF,INF,11, INF,INF,INF, 10, 0, 18, INF,INF,INF,16, INF,12, INF,INF,0, 22, INF,INF,INF,INF,8, INF,INF,22, 0, 20, INF,INF,16, 21, INF,INF,INF,20, 0, 26, INF,7, INF, 11, INF,INF,INF,26, 0, 17, INF,INF, INF,16, INF,INF,INF,17, 0, 19, INF, INF,INF,INF,16, 7, INF,19, 0, INF, INF,12, 8, 21, INF,INF,INF,INF,0}; void bubblesort(Graph *g,int len); void swap(Graph *g,int i,int j); int find(int *p,int n); int main(){ int parent[20] = {0}; int i,j,k,n,m; int max=0; int flag = 1; Graph *g = (Graph *)malloc(sizeof(Graph)); for(i=0;i<MAXSIZE;i++){ for(j=0;j<MAXSIZE;j++){ flag = 1; if(i != j && num[i][j] != INF){ for(k=0;k<=max;k++){ if(g->e[k].begin == j && g->e[k].end == i){ flag = 0; break; } } if( flag ){ g->e[max].begin = i; g->e[max].end = j; g->e[max].length = num[i][j]; //printf("[%d]%d %d %d \n",max,g->e[max].begin,g->e[max].end,g->e[max].length); max++; } } } } printf("\n"); bubblesort(g,max); for(i=0;i<max;i++){ printf("%d %d %d \n",g->e[i].begin,g->e[i].end,g->e[i].length); } for(i=0;i<max;i++){ n = find(parent,g->e[i].begin); m = find(parent,g->e[i].end); if(n != m){ parent[n] = m; printf("[%d %d] %d \n",g->e[i].begin,g->e[i].end,g->e[i].length); } } getchar(); return 0; } int find(int * p,int n){ while(p[n] > 0) n = p[n]; return n; } void bubblesort(Graph *g,int len){ int i,j; for(i=0; i < len; i++){ for(j = len-1; j>i; j--){ if(g->e[j].length < g->e[i].length){ swap(g,i,j); } } } } void swap(Graph *g,int i,int j){ edge *pool = (edge *)malloc(sizeof(edge)); pool->begin = g->e[j].begin; pool->end = g->e[j].end; pool->length = g->e[j].length; g->e[j].begin = g->e[i].begin; g->e[j].end = g->e[i].end; g->e[j].length = g->e[i].length; g->e[i].begin = pool->begin; g->e[i].end = pool->end; g->e[i].length = pool->length; free(pool); }
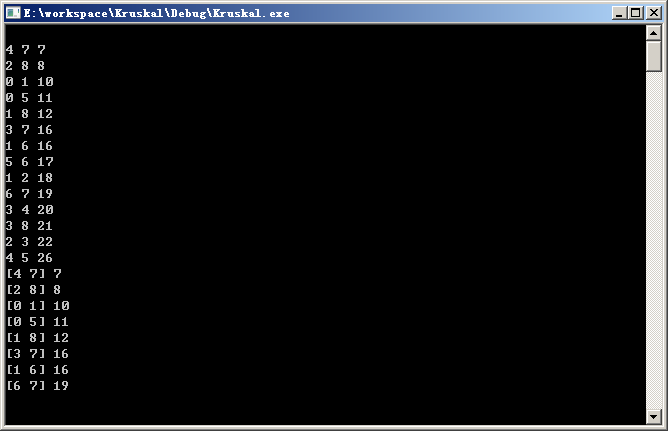
运行结果