APG(Accelerate Proximal Gradient)加速近端梯度算法 和 NAG(Nesterov accelerated gradient)优化器原理 (一)
文章目录
- 前言
- APG(Accelerate Proximal Gradient)加速近端梯度算法[^1]
-
- PGD (Proximal Gradient Descent)近端梯度下降法推导[^2]
-
- Example of Proximal Gradient Descent
- APG(Accelerate Proximal Gradient)加速近端梯度算法推导
-
- Back to lasso example:
- 总结
- 引用
前言
近期在阅读Data-Driven Sparse Structure Selection for Deep Neural Networks论文时,用到里面APG-NAG相关优化器的知识,原论文方法采用mxnet去实现的,在这里想迁移到pytorch中。因此手撕一下APG和NAG相关的知识。
APG(Accelerate Proximal Gradient)加速近端梯度算法1
该方法是近端梯度下降法(Proximal Gradient Descent)的一种扩展方法,溯源的话应该早于2008年。在了解APG方法之前,首先需要了解一下近端梯度下降法(Proximal Gradient Descent).
PGD (Proximal Gradient Descent)近端梯度下降法推导2
直接套用Chen Xin Yu2的原话:“近端梯度下降法是众多梯度下降 (gradient descent) 方法中的一种,其英文名称为proximal gradident descent,其中,术语中的proximal一词比较耐人寻味,将proximal翻译成“近端”主要想表达”(物理上的)接近"。与经典的梯度下降法和随机梯度下降法相比,近端梯度下降法的适用范围相对狭窄。对于凸优化问题,当其目标函数存在不可微部分(例如目标函数中有 1-范数或迹范数)时,近端梯度下降法才会派上用场。"
近端梯度下降法(Proximal Gradient Descent)主要用于解决目标函数中包含不可微的凸函数的问题。即,假定存在,
f ( x ) = g ( x ) + h ( x ) \begin{align} f(x)=g(x)+h(x) \end{align} f(x)=g(x)+h(x)
其中
- g ( x ) g(x) g(x)是可微分的凸函数,且 d o m ( g ) = R n dom(g)=\mathbb{R}^n dom(g)=Rn
- h ( x ) h(x) h(x)不是必须可微的凸函数,即可以可微,也可以不可微,也可以局部可微。
我们的目标是,
min x f ( x ) = g ( x ) + h ( x ) \begin{align} \min_{x}f(x)=g(x)+h(x) \end{align} xminf(x)=g(x)+h(x)
如果 f f f可微的话,则非常简单,直接用梯度下降法就可以实现,即,
x + = x − t ∇ f ( x ) \begin{align} x^+=x- t \nabla f(x) \end{align} x+=x−t∇f(x)
此处 t t t可等价为学习率。
且可通过最小化函数 f f f在 x x x周围的二阶近似(Minimize quadratic approximation to f f f around x x x),来找到 x + x^+ x+,且可将其二阶导数 ∇ 2 f ( x ) \nabla^2f(x) ∇2f(x)替换为 1 t \frac{1}{t} t1,表示如下:
x + = arg min z f ( x ) + ∇ f ( x ) T ( z − x ) + 1 2 t ∣ ∣ z − x ∣ ∣ 2 2 = arg min z f ˉ t ( z ) \begin{align} x^+=\argmin_{z} f(x)+\nabla f(x)^T (z-x) + \frac{1}{2t}||z-x||^2_2 = \argmin_{z} \bar{f}_t(z) \end{align} x+=zargminf(x)+∇f(x)T(z−x)+2t1∣∣z−x∣∣22=zargminfˉt(z)
(注意:这里不是很明确为什么可以这样替换,仅知道是泰勒展开的形式,有理解的可以告诉我一下。而且作者为什么能想到上一步也不是很明晰)
然而,由于 h ( x ) h(x) h(x)的存在,函数 f ( x ) f(x) f(x)并不一定可微,但是注意 g ( x ) g(x) g(x)是可微的。因此,我们可以将 h ( x ) h(x) h(x)单独拿出来,并仅对 g ( x ) g(x) g(x)进行二阶近似,即,
x + = arg min z g t ˉ ( z ) + h ( z ) = arg min z g ( x ) + ∇ g ( x ) T ( z − x ) + 1 2 t ∣ ∣ z − x ∣ ∣ 2 2 + h ( z ) = arg min z 1 2 t ∣ ∣ z − ( x − t ∇ g ( x ) ) ∣ ∣ 2 2 + h ( z ) \begin{align} x^+ &= \argmin_z \bar{g_t}(z) + h(z) \nonumber \\ ~&= \argmin_z g(x)+\nabla g(x)^T (z-x) + \frac{1}{2t}||z-x||^2_2 + h(z) \nonumber \\ ~&= \argmin_z \frac{1}{2t}||z-(x-t\nabla g(x))||^2_2+h(z) \\ \end{align} x+ =zargmingtˉ(z)+h(z)=zargming(x)+∇g(x)T(z−x)+2t1∣∣z−x∣∣22+h(z)=zargmin2t1∣∣z−(x−t∇g(x))∣∣22+h(z)
上述具体详细推导可见:近端梯度下降算法(Proximal Gradient Algorithm),提示:z是变量,z之外的常数项可以去掉或添加,不影响z的改变。
则为了最小化公式(5),即一方面另 z z z尽可能靠近 ( x − t ∇ g ( x ) ) (x-t\nabla g(x)) (x−t∇g(x)) (对g(x),尽可能靠近梯度下降方向),另一方面另 h ( z ) h(z) h(z)尽可能小。
则可以定义Proximal operator(近端算子)如下,
p r o x h , t ( x ) = arg min z 1 2 t ∣ ∣ x − z ∣ ∣ 2 2 + h ( z ) \begin{align} prox_{h,t}(x) = \argmin_{z} \frac{1}{2t}||x-z||^2_2+ h(z) \end{align} proxh,t(x)=zargmin2t1∣∣x−z∣∣22+h(z)
因此近端梯度下降法(Proximal Gradient Descent)可表示为: 对于 f ( x ) = g ( x ) + h ( x ) f(x)=g(x)+h(x) f(x)=g(x)+h(x),给定任意初始化 x ( 0 ) x^(0) x(0),重复如下步骤即可得到近似最优 x ∗ x^* x∗,
x ( k ) = p r o x h , t k ( x ( k − 1 ) − t k ∇ g ( x ( k − 1 ) ) ) , k = 1 , 2 , 3 , … \begin{align} x^{(k)}=prox_{h,t_k}(x^{(k-1)}-t_k\nabla g(x^{(k-1)})) , \space k=1,2,3,\ldots \end{align} x(k)=proxh,tk(x(k−1)−tk∇g(x(k−1))), k=1,2,3,…
至此,近端梯度下降法(Proximal Gradient Descent)推到完毕(收敛性分析略过,感兴趣同学可以参考cmu的PPT)。可能有读者有些许疑惑,为什么要做这么大一堆操作?不最后还是要最小化 h ( z ) h(z) h(z)吗?并没有讲不可微函数 h ( x ) h(x) h(x)是如何通过梯度下降来求解的哇。
然而,近端梯度下降法(Proximal Gradient Descent)主要亮点在如下方面:
- Proximal operator(近端算子)不再依赖 g ( x ) g(x) g(x),仅依赖于 h ( x ) h(x) h(x)。也就是说,本来 f ( x ) = g ( x ) + h ( x ) f(x)=g(x)+h(x) f(x)=g(x)+h(x)可以是一个非常复杂的可微分函数和一个不那么复杂的不可微分函数的组合,但使用该方法,我们无需考虑 g ( x ) g(x) g(x)(因为其可微分,梯度很好计算),仅需针对性考虑不可微分函数 h ( x ) h(x) h(x)即可,极大的简化了我们的问题。
总结+个人理解:这里原本想画图解释一下近端梯度下降法(Proximal Gradient Descent),但发现不是很好画,就简单用文字表述一下我对Proximal (近端)的理解, 理想情况下,梯度下降方向朝向是我们目标函数最优方向,但由于函数存在不可微分项,因此梯度下降的方向无法确定(虽然不可微分函数存在次梯度这一说(例如L1范数存在次梯度),但f(x)整体梯度如果始终包含不可微分的函数的次微分的话,实际梯度与计算梯度将始终有一定偏差,随着迭代次数过多后,偏差更大。)。所以,我们将可微分项和不可微分项拿出来,首先确保我们的可微分项的梯度下降方向绝对正确,不可微分项再另想办法进行最小化,这种思想就是PGD的思想。个人认为Proximal(近端)主要有一种近似(接近)的含义在里面,而且表现在梯度的近端上,更进一步,主要表现在可微分项梯度和不可微分项的梯度与整体函数梯度的近端(接近程度)上。
Example of Proximal Gradient Descent
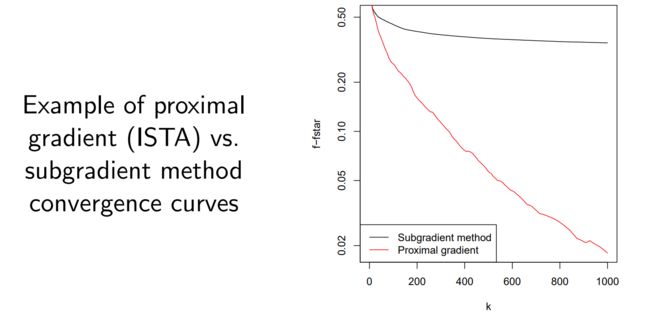
参考CMU的PPT,也举一个例子,ISTA算法,便于更加直观的理解:
Lasso criterion 一篇对lasso的讲解,感觉非常不错
定义如下函数:
f ( β ) = 1 2 ∣ ∣ y − X β ∣ ∣ 2 2 + λ ∣ ∣ β ∣ ∣ 1 \begin{align} f(\beta)= \frac{1}{2} ||y-X\beta||^2_2 + \lambda ||\beta||_1\end{align} f(β)=21∣∣y−Xβ∣∣22+λ∣∣β∣∣1
即其 min β f ( β ) \min_{\beta} f(\beta) minβf(β)如图所示,
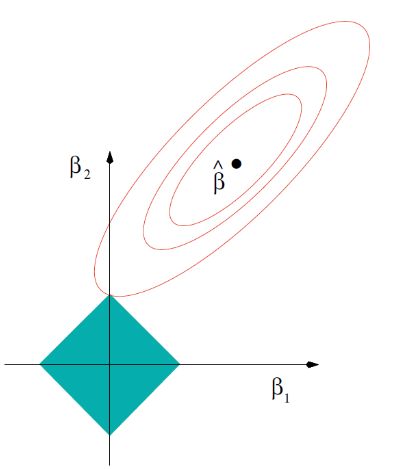
上述公式就是一个典型的近端梯度下降算法(Proximal Gradient Algorithm)问题,可看作 g ( β ) = 1 2 ∣ ∣ y − X β ∣ ∣ 2 2 g(\beta)= \frac{1}{2} ||y-X\beta||^2_2 g(β)=21∣∣y−Xβ∣∣22, h ( β ) = λ ∣ ∣ β ∣ ∣ 1 h(\beta)=\lambda ||\beta||_1 h(β)=λ∣∣β∣∣1。
则引入我们的近端算子(Proximal operator),
p r o x t = arg min z 1 2 t ∣ ∣ β − z ∣ ∣ 2 2 + λ ∣ ∣ z ∣ ∣ 1 = S λ t ( β ) \begin{align} prox_{t} &=\argmin_{z} \frac{1}{2t}||\beta-z||^2_2+ \lambda ||z||_1 \nonumber \\ &=S_{\lambda t}(\beta)\end{align} proxt=zargmin2t1∣∣β−z∣∣22+λ∣∣z∣∣1=Sλt(β)
其中, S λ t ( β ) S_{\lambda t}(\beta) Sλt(β)也称为 soft-thresholding operator,具体如下:
[ S λ ( β ) ] i = { β i − λ if β i > λ 0 if − λ ≤ β i ≤ λ , i = 1 , … , n β i + λ if β i < − λ \begin{equation} \left[S_\lambda(\beta)\right]_i= \begin{cases}\beta_i-\lambda & \text { if } \beta_i>\lambda \\ 0 & \text { if }-\lambda \leq \beta_i \leq \lambda, \quad i=1, \ldots, n \\ \beta_i+\lambda & \text { if } \beta_i<-\lambda\end{cases} \end{equation} [Sλ(β)]i=⎩ ⎨ ⎧βi−λ0βi+λ if βi>λ if −λ≤βi≤λ,i=1,…,n if βi<−λ
有关soft-thresholding operator如何这样设计可见https://angms.science/doc/CVX/ISTA0.pdf,参考自知乎,我也实在推不动了。
则我们按照公式(7)的方法,已知 ∇ g ( β ) = − X T ( y − X β ) \nabla g(\beta)=-X^T(y-X\beta) ∇g(β)=−XT(y−Xβ),则,给定初始化 β 0 \beta^0 β0
β ( k ) = p r o x h , t k ( β ( k − 1 ) − t k ∇ g ( β ( k − 1 ) ) ) , k = 1 , 2 , 3 , … = S λ t k ( β ( k − 1 ) + t k X T ( y − X β ( k − 1 ) ) ) \begin{align} \beta^{(k)}&=prox_{h,t_k}(\beta^{(k-1)}-t_k\nabla g(\beta^{(k-1)})) , \space k=1,2,3,\ldots \\ &=S_{\lambda t_k}(\beta^{(k-1)}+t_k X^T(y-X\beta^{(k-1)})) \end{align} β(k)=proxh,tk(β(k−1)−tk∇g(β(k−1))), k=1,2,3,…=Sλtk(β(k−1)+tkXT(y−Xβ(k−1)))
至此,随着k的迭代,可得到近似最优 β ∗ \beta^* β∗
12点半了,回宿舍,明天更
同时,该方法也被称为 iterative soft-thresholding algorithm (ISTA).
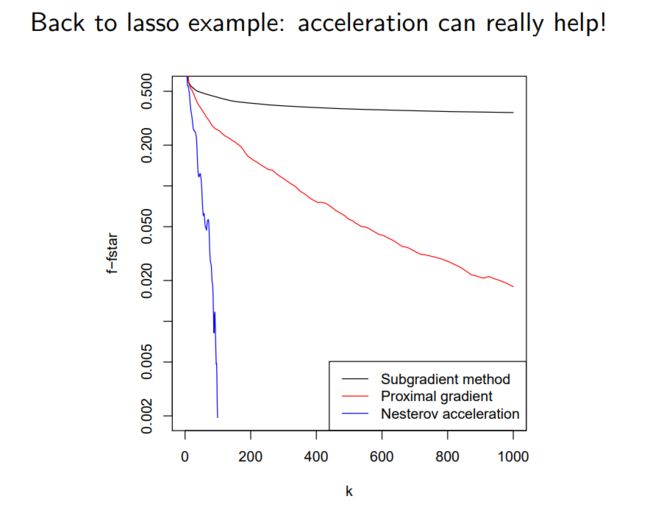
如下图1,与直接将 f ( x ) f(x) f(x)求次梯度的方法相比,该方法可以有效收敛。
APG(Accelerate Proximal Gradient)加速近端梯度算法推导
如果对PGD有一个清晰的认识后,那么APG的推导将变会变得无比清晰简单,再次重复一下我们的目标,
min x f ( x ) = g ( x ) + h ( x ) \begin{align} \min_{x}f(x)=g(x)+h(x) \end{align} xminf(x)=g(x)+h(x)
其中
- g ( x ) g(x) g(x)是可微分的凸函数,且 d o m ( g ) = R n dom(g)=\mathbb{R}^n dom(g)=Rn
- h ( x ) h(x) h(x)不是必须可微的凸函数,即可以可微,也可以不可微,也可以局部可微。
在之前PGD方法中,最重要的是公式(7),而APG方法也仅在公式(7)的输入上做了一个大家非常熟悉的改动,如下所示,给定初始化 x ( 0 ) x^{(0)} x(0),且另 x ( − 1 ) = x ( 0 ) x^{(-1)}=x^{(0)} x(−1)=x(0)(这一步仅为了公式美观,无别的意义),则:
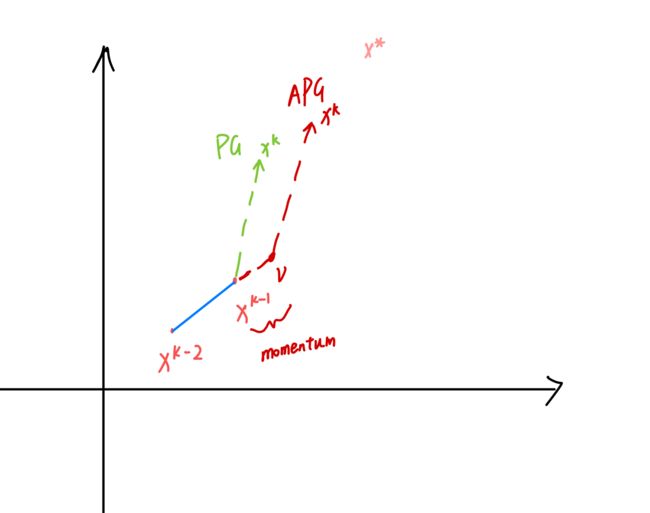
v = x ( k − 1 ) + k − 2 k + 1 ( x ( k − 1 ) − x ( k − 2 ) ) x ( k ) = prox t k ( v − t k ∇ g ( v ) ) f o r k = 1 , 2 , 3 , … \begin{align} v &=x^{(k-1)}+\frac{k-2}{k+1}\left(x^{(k-1)}-x^{(k-2)}\right) \\ x^{(k)} &=\operatorname{prox}_{t_k}\left(v-t_k \nabla g(v)\right) \\ for \space k=1,2,3, \ldots \nonumber \end{align} vx(k)for k=1,2,3,…=x(k−1)+k+1k−2(x(k−1)−x(k−2))=proxtk(v−tk∇g(v))
- 对于k=1时,为PGD算法。
- 对于k>1时,相当于 x ( k − 1 ) x^{(k-1)} x(k−1)加了一个动量,变成 v v v。
- 如果 h ( x ) h(x) h(x)不存在,即 f ( x ) f(x) f(x)可微,则相当于梯度下降算法。
公式(15)等同于公式(7),公式(14)就是增加一个小的动量,以此达到加速的目的。如下图所示:
Back to lasso example:
总结
PGD和APG主要用于目标函数中存在不可微分项的情况,在实际的深度学习算法中,该情况最主要用于稀疏优化,例如损失函数增加架构参数的L1范数,可以使架构参数变得稀疏。当然,该方法也有许多其它应用,总之,当你的函数中出现不可微分问题的时候,就可以来参考一下PGD算法。
后续NAG优化器原理将放在(二)中 (二)的链接,太长了,拆一拆。后续部分会讲解NAG优化器,以及论文中如何将APG和NAG结合到一起,并尝试给出pytorch自定义优化器的代码实现(原论文是Mxnet)。
引用
Proximal Gradient Descent (and Acceleration) link: https://www.stat.cmu.edu/~ryantibs/convexopt/lectures/prox-grad.pdf (强推!) ↩︎ ↩︎
机器学习 | 近端梯度下降法 (proximal gradient descent) (强推!) ↩︎ ↩︎