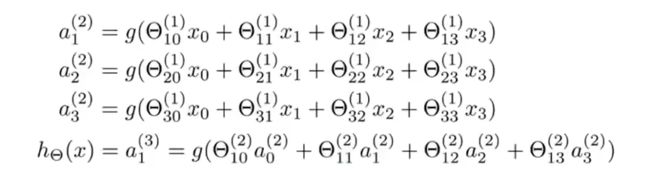吴恩达ML WEEK6 练习三(神经网络)+神经网络学习
吴恩达机器学习 第六周
- 0 总结
- 1 练习三:神经网络
-
- 1.1 前向传播和预测
- 2 神经网络学习
-
- 2.1 代价函数
- 2.2 反向传播算法
- 2.3 理解反向传播
- 2.4 展开参数(将矩阵展开成向量)
- 2.5 梯度检验
- 2.6 随机初始化
- 2.7 综合
0 总结
学习时间:2022.10.10~2022.10.16
- 完成练习三:神经网络的前向传播算法
- 学习神经网络的代价函数
- 学习并理解神经网络反向传播算法
- 自学了反向传播公式的推导过程
- 学习神经网络梯度检验方法和权重矩阵的随机初始化
1 练习三:神经网络
1.1 前向传播和预测
任务:完成predict.py
代码:
def predict(theta1, theta2, x):
# Useful values
m = x.shape[0]
num_labels = theta2.shape[0]
# You need to return the following variable correctly
p = np.zeros(m)
# ===================== Your Code Here =====================
# Instructions : Complete the following code to make predictions using
# your learned neural network. You should set p to a
# 1-D array containing labels between 1 to num_labels.
#
x = np.c_[np.ones(m),x]
a_2 = sigmoid(np.dot(x,theta1.T))
a_2 = np.c_[np.ones(m),a_2]
a_3 = sigmoid(np.dot(a_2,theta2.T))
p = np.argmax(a_3,axis = 1)
p += 1
return p
2 神经网络学习
2.1 代价函数
Layer1:输入层,Layer2:隐藏层(可不止一层),Layer3:输出层。
a i j a_i^j aij:第 j j j层的第 i i i个节点。(上角标表示层数)
Θ j \Theta^j Θj:第 j j j层到第 j + 1 j+1 j+1层的权重。
如果神经网络在第 j j j层有 s j s_j sj个单元,在第 j + 1 j+1 j+1层有 s j + 1 s_{j+1} sj+1个单元,那么 Θ j = s j + 1 × ( s j + 1 ) \Theta_j=s_{j+1}\times(s_j+1) Θj=sj+1×(sj+1)(不包含1),比如这里, Θ 1 ∈ R 3 × 4 \Theta_1\in\mathbb{R}^{3\times4} Θ1∈R3×4
要注意,正则项也是不包括 i = 0 i=0 i=0的!
2.2 反向传播算法
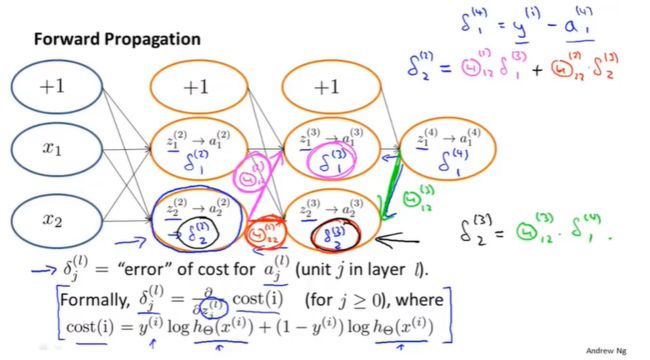
复习前向传播
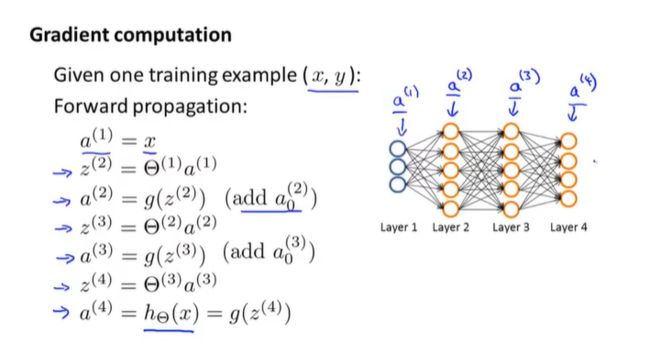
梯度计算
本质:对于神经网络的每一个节点(除了输出节点),计算 δ j ( l ) \delta_j^{(l)} δj(l),即:第 l l l层第 j j j个节点的误差。( a j ( l ) a_j^{(l)} aj(l)表示的是第 l l l层第 j j j个节点的激活值,所以 δ j ( l ) \delta_j^{(l)} δj(l)在某种程度上捕捉了第 l l l层第 j j j个节点的激活值的误差)
以上面四层的神经网络为例:
δ ( 4 ) = a ( 4 ) − y δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) . ∗ g ′ ( z ( 3 ) ) = ( Θ ( 3 ) ) T δ ( 4 ) . ∗ a ( 3 ) . ∗ ( 1 − a ( 3 ) ) δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) . ∗ g ′ ( z ( 2 ) ) = ( Θ ( 2 ) ) T δ ( 3 ) . ∗ a ( 2 ) . ∗ ( 1 − a ( 2 ) ) n o δ ( 1 ) ∂ J ( Θ ) ∂ Θ i j ( l ) = a j ( l ) δ i ( l + 1 ) ( P S : 忽略正则项 ) \begin{align} &\delta^{(4)}=a^{(4)}-y \notag \\ &\delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)}.*g^{'}(z^{(3)})=(\Theta^{(3)})^T\delta^{(4)}.*a^{(3)}.*(1-a^{(3)}) \notag \\ &\delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g^{'}(z^{(2)})=(\Theta^{(2)})^T\delta^{(3)}.*a^{(2)}.*(1-a^{(2)}) \notag \\ &no\ \delta^{(1)} \notag \\ &\frac{\partial J(\Theta) }{\partial \Theta^{(l)}_{ij}} = a^{(l)}_j\delta^{(l+1)}_i(PS:忽略正则项) \notag \end{align} δ(4)=a(4)−yδ(3)=(Θ(3))Tδ(4).∗g′(z(3))=(Θ(3))Tδ(4).∗a(3).∗(1−a(3))δ(2)=(Θ(2))Tδ(3).∗g′(z(2))=(Θ(2))Tδ(3).∗a(2).∗(1−a(2))no δ(1)∂Θij(l)∂J(Θ)=aj(l)δi(l+1)(PS:忽略正则项)
推导可参考: 反向传播算法推导
反向传播
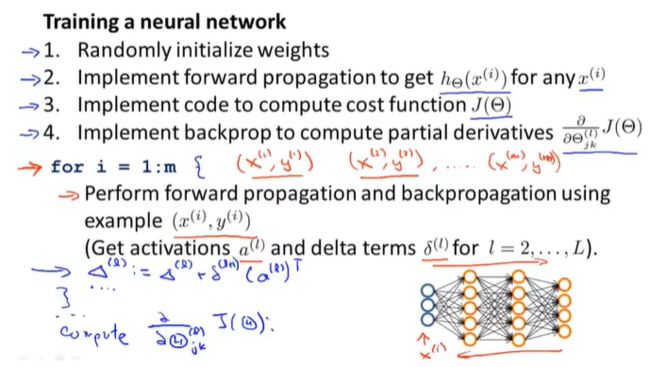
训练集: { ( x ( 1 ) , y ( 1 ) ) , . . . , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})\} {(x(1),y(1)),...,(x(m),y(m))}
对每个 l , i , j l,i,j l,i,j设: Δ i j ( l ) = 0 \Delta^{(l)}_{ij}=0 Δij(l)=0
F o r i = 1 t o m S e t a ( 1 ) = x ( i ) 前向回归计算 a ( l ) ( l = 2 , 3 , . . . , L ) 使用 y ( i ) ,计算 δ ( L ) = a ( L ) − y ( i ) 计算 δ ( L − 1 ) , δ ( L − 2 ) , . . . , δ ( 2 ) Δ i j ( l ) : = Δ i j ( l ) + a j ( l ) δ i ( l + 1 ) \begin{align} For\ i=1\ to\ m \notag\\ &Set\ a^{(1)}=x^{(i)}\notag\\ &前向回归计算a^{(l)}(l=2,3,...,L)\notag\\ &使用y^{(i)},计算\delta^{(L)}=a^{(L)}-y^{(i)}\notag\\ &计算\delta^{(L-1)},\delta^{(L-2)},...,\delta^{(2)}\notag\\ &\Delta^{(l)}_{ij}:=\Delta^{(l)}_{ij}+a^{(l)}_j\delta^{(l+1)}_i\notag\\ \end{align} For i=1 to mSet a(1)=x(i)前向回归计算a(l)(l=2,3,...,L)使用y(i),计算δ(L)=a(L)−y(i)计算δ(L−1),δ(L−2),...,δ(2)Δij(l):=Δij(l)+aj(l)δi(l+1)
循环结束后:
D i j ( l ) : = 1 m Δ i j ( l ) + λ m Θ i j ( l ) i f j ≠ 0 D i j ( l ) : = 1 m Δ i j ( l ) i f j = 0 ∂ J ( Θ ) ∂ Θ i j ( l ) = D i j ( l ) \begin{align} &D^{(l)}_{ij}:=\frac{1}{m}\Delta^{(l)}_{ij}+\frac{\lambda}{m}\Theta^{(l)}_{ij}\ if\ j\neq0\notag\\ &D^{(l)}_{ij}:=\frac{1}{m}\Delta^{(l)}_{ij}\ if\ j=0\notag\\ &\frac{\partial J(\Theta) }{\partial \Theta^{(l)}_{ij}} =D^{(l)}_{ij}\notag \end{align} Dij(l):=m1Δij(l)+mλΘij(l) if j=0Dij(l):=m1Δij(l) if j=0∂Θij(l)∂J(Θ)=Dij(l)
2.3 理解反向传播
a = s i g m o i d ( z ) a=sigmoid(z) a=sigmoid(z)
以第 i i i个样本为例, c o s t ( i ) cost(i) cost(i)可以理解为:
预测输出与实际输出的差值,表示了预测值和实际值的接近程度。只是在逻辑回归中比较倾向于选择带对数的代价函数。
反向传播就是在计算这些 δ j ( l ) \delta^{(l)}_j δj(l)项。
2.4 展开参数(将矩阵展开成向量)
在逻辑回归时,我们定义了一个计算损失的函数 c o s t F u n c t i o n costFunction costFunction,它的输入是 θ \theta θ,输出是梯度和损失。将 c o s t F u n c t i o n costFunction costFunction、初始的 θ \theta θ值作为 f m i n u n c fminunc fminunc的参数。在这里, θ \theta θ和梯度都是n+1的向量(假设有n个特征)。
在神经网络中,我们的参数不在是向量了,而是矩阵 。对于一个四层的神经网络我们定义:
Θ ( 1 ) , Θ ( 2 ) , Θ ( 3 ) 在代码中记为: T h e t a 1 , T h e t a 2 , T h e t a 3 \Theta^{(1)},\Theta^{(2)},\Theta^{(3)}在代码中记为:Theta1,Theta2,Theta3 Θ(1),Θ(2),Θ(3)在代码中记为:Theta1,Theta2,Theta3 D ( 1 ) , D ( 2 ) , D ( 3 ) 在代码中记为: D 1 , D 2 , D 3 D^{(1)},D^{(2)},D^{(3)}在代码中记为:D1,D2,D3 D(1),D(2),D(3)在代码中记为:D1,D2,D3
2.5 梯度检验
假设只有一个 θ \theta θ,那么如图所示,可以近似认为代价函数对 θ \theta θ求导公式(双侧差分two-side difference): ∂ J ( θ ) ∂ θ ≈ J ( θ + ϵ ) − J ( θ − ϵ ) 2 ϵ \frac{\partial J(\theta)}{\partial \theta}\approx \frac{J(\theta+\epsilon)-J(\theta-\epsilon)}{2\epsilon} ∂θ∂J(θ)≈2ϵJ(θ+ϵ)−J(θ−ϵ),其中, ϵ \epsilon ϵ一般取 1 0 − 4 10^{-4} 10−4(太小了不好)。
θ \theta θ是一个n维的向量(是矩阵 Θ ( 1 ) , Θ ( 2 ) , Θ ( 3 ) \Theta^{(1)},\Theta^{(2)},\Theta^{(3)} Θ(1),Θ(2),Θ(3)的展开),我们可以用上述相似的思想来估计所有的偏导项,如图所示。
如果我们用这种思想求得的偏导数gradApprox,和我们在反向传播中得到的梯度Dvec(代价函数关于所有参数的导数)近似相等,那么可以确信,反向传播的实现是正确的。
总结
步骤一:利用反向传播算法计算 D V e c DVec DVec(矩阵 D ( 1 ) , D ( 2 ) , D ( 3 ) D^{(1)},D^{(2)},D^{(3)} D(1),D(2),D(3)的展开)。
步骤二:实现数值上的梯度检验,计算出 g r a d A p p r o x gradApprox gradApprox。
步骤三:保证 D V e c DVec DVec和 g r a d A p p r o x gradApprox gradApprox近似。
步骤四:关掉梯度检查,使用反向传播算法。
Tips:
在训练分类器之前要保证关闭了梯度检查代码。因为如果在每次爹地啊过程中都使用了数值上的梯度检验,代码将会运行得很慢。
2.6 随机初始化
会导致图中蓝色的线相等、红色的线相等、绿色的线相等,最后导致隐藏的每一个神经元都是一样的,所以特征值也是一样的,也就是只有一个特征。
rand(10,11)表示生成一个10*11的矩阵,矩阵中每个数在0到1之间
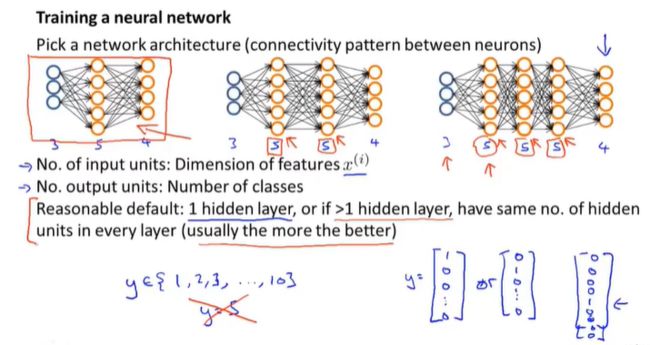
2.7 综合
输入单元的个数= x ( i ) x^{(i)} x(i)(第i个输入样本)的特征的维度
输出单元的个数=类别的个数
如果使用不止一个的隐藏层,那么隐藏层单元的个数应该相等。通常情况下,隐藏单元越多越好,但是隐藏单元越多,计算量越大。每一个隐藏层的单元个数,通常取特征数倍数。
①初始化权重矩阵(通常取很接近0的数)。
②执行前向传播算法,计算出每一个输入样本的 h Θ ( x ( i ) ) h_\Theta(x^{(i)}) hΘ(x(i))。
③执行代价函数算法,计算得 J ( Θ ) J(\Theta) J(Θ)。
④执行反向传播算法,计算出偏导数 ∂ J ( Θ ) ∂ Θ j k ( l ) \frac {\partial J(\Theta)}{\partial \Theta^{(l)}_{jk}} ∂Θjk(l)∂J(Θ)
⑤执行梯度检查,检查反向传播算法的正确性后,关闭梯度检查代码。
⑥使用梯度下降或者其他更高级的算法,使得代价函数最小化。