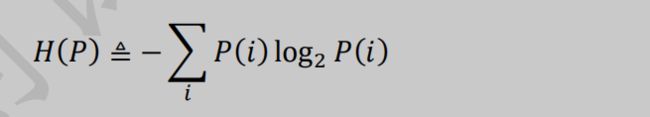神经网络的相关函数以及误差类型
A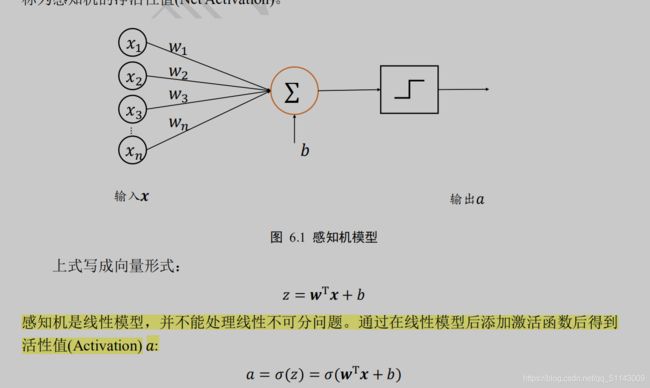
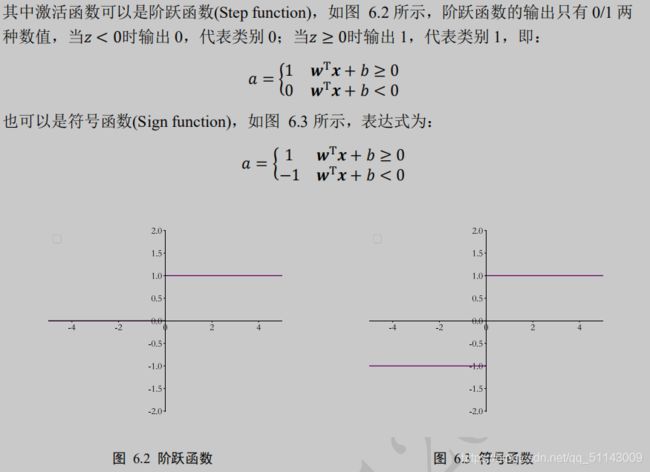
以感知机为代表的线性模型不能解决异或(XOR)等线性不可分问题，但是可以用嵌套多层神经网络解决
激活函数，与阶跃函数和符号函数不同，这些函数都是平滑可导的，适合于梯度下降算法。
1.Sigmoid 函数在输入值较大或较小时容易出现梯度值接近于 0 的现象，称为梯度弥散现象。出现梯度弥散现象时，网络参数长时间得不到更新，
导致训练不收敛或停滞不动的现象发生，较深层次的网络模型中更容易出现梯度弥散现象。
2tanh函数
ReLU 函数的导数计算简单，x 大于等于零的时候，导数值恒为 1，在反向传播过程中，它既不会放大梯度，造成梯度爆炸(Gradient exploding)现象；也不会缩小梯度，造成梯度弥散(Gradient vanishing)现象。
（神经网络中激活函数采用 Sigmoid 居多，但是 Sigmoid函数容易出现梯度弥散现象，当网络的层数增加后，较前层的参数由于梯度值非常微小，）
B
输出层的设计：（6.5）
1.普通实数空间，像正弦函数曲线预测、年龄的预测、股票走势的预测等都属于
整个或者部分连续的实数空间，输出层可以不加激活函数。误差的计算直接基于最后一层的输出和真实值进行计算，如采用均方差误差函数度量输出值与真实值之间的距离： ℒ = (,) 其中代表了某个具体的误差计算函数，例如 MSE 等
2.输出值属于[0,1]区间也比较常见，比如图片的生成、二分类问题等。在机器学习中，一般会将图片的像素值归一化到[0,1]区间，如果直接使用输出层的值，像素的值范围会分布在整个实数空间。
同样地，对于二分类问题，如硬币的正反面的预测，输出层可以只设置一个节点，
表示某个事件 A 发生的概率(A|)，为网络输入。
3.[0,1]区间，和为 1，运用于多分类网络结构
4.如果希望输出值的范围分布在(−1,1)区间，可以简单地使用 tanh 激活函数
C误差计算（6.6）
1.均方差(Mean Squared Error，简称 MSE)误差函数把输出向量和真实向量映射到笛卡尔坐标系的两个点上，通过计算这两个点之间的欧式距离(准确地说是欧式距离的平方)来衡量两个向量之间的间距
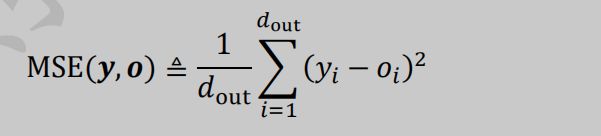
MSE 误差函数的值总是大于等于 0，当 MSE 函数达到最小值 0 时，输出等于真实标签，此时神经网络的参数达到最优状态。
2.交叉熵误差函数（衡量信息的不确定度）
熵越大，不确定性越大，信息量越大
对于确定的分布，熵为 0，不确定性最低。
