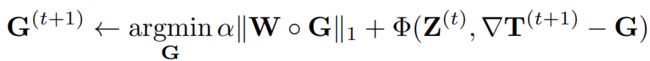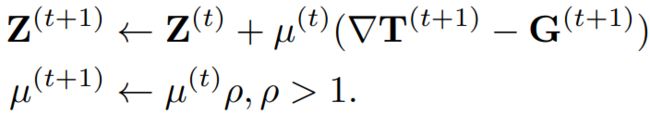LIME Low light Image Enhancement via Illumination Map Estimation

LIME: Low-light Image Enhancement via Illumination Map Estimation

0 Abstract and Introduction

通过寻找RGB三通道中的最大值，并分别估计每个像素的illumination，然后添加一个结构来完善initial illumination map 来作为最终的illumination map。

该方法具有LIME的有效性，并具有很好的图像增强效果和效率。

高可见度的图像具有目标场景的具体细节，low-light情况下的图像可见度低，

Contribution:

基于Retinex策略估计illumination map来增强低光照。本方法只估计illumination 缩小solution space并减少计算成本。

1.求解RGB三通道每个像素的最大强度来构造illumination map，使用illumination structure 来构造illumination map。

2.采用An Augmented Lagrangian Multiplier (ALM)算法来求解优化问题，并设计sped-up solver减少计算量，

1 Methodology

基于Retinex模型：

$L=R\circ T$ ------》model （1）

L是捕捉图片。

R是desired recovery。

T是illumination map。

$\circ$是 element-wise multiplication.

对于彩色图像，三通道共享illumination map，使用$T(\hat{T})$交替表示一个通道和三通道illumination map。

model （1）物理意义：the observed image 能被分解为the desired light-enhanced scene 和the illumination map。

The instrinsic image decomposition的目的是从给定图像中恢复给定图像中the reflectance 分量和the shading 分量。

As shown in Fig.3 b 中 the reflectance 缺少盒子形状。c能recall 黑暗区域的视觉内容，同时保持视觉的真实感。

使用the reflectance 作为增强结果，并使用modified illumination 返回到the reflectance，

本方法对低光照图片进行调亮。通过$L=R\circ T$ 使用$R=R/T$ （对元素进行除法）$T$的估计是$R$恢复的关键，估计值为$\hat{T}$，增强结果为$L/\hat{T}$。

A Illumination Map Estimation

Max-RGB（颜色恒常性）通过求解RGB的最大值来估计光照。

为了处理非均匀光照，交替采用

$\hat{T}(x)\leftarrow \underset{c\in \left\{R,G,B\right\}}{\max }{L}^c(x)$ 意义为 在某一位置，illumination至少是三通道的最大值。

因为$R(x)=L(x)/(\underset{c}{\max }{L}^c(x)+\epsilon )$得到的$\hat{T}(x)$保证恢复不会饱和，$\epsilon$ 是防止分母为零。

基于inverted low-light 图片$1—L$ 与haze 雾霾图像的观察：$1-L=(1-R)\circ T+a(1-T)$，$a$为global atmosphere light,

暗通道先验（the dark channel prior）用于估计去雾传输图的先验：$T(x)\leftarrow 1-\underset{c}{\min }\frac{1-L^c(x)}{a}=1-\frac{1}{a}+\underset{c}{\max }\frac{L^c(x)}{a}$

代入$T(x)\leftarrow 1-\underset{c}{\min }\frac{1-L^c(x)}{a}=1-\frac{1}{a}+\underset{c}{\max }\frac{L^c(x)}{a}$到$1-L=(1-R)\circ T+a(1-T)$里去：

$R(x)=\frac{L(x)-1+a}{1-\frac{1}{a}+\underset{c}{\max }\frac{L^c(x)}{a}+\epsilon }+(1+a)$

$a=1$， $R(x)=L(x)/(\underset{c}{\max }{L}^c(x)+\epsilon )$和$R(x)=\frac{L(x)-1+a}{1-\frac{1}{a}+\underset{c}{\max }\frac{L^c(x)}{a}+\epsilon }$达到相同结果，当a不为1时，则结果不同。

the atmosphere light 大于0.95，the $R(x)=\frac{L(x)-1+a}{1-\frac{1}{a}+\underset{c}{\max }\frac{L^c(x)}{a}+\epsilon }+(1+a)$ and $R(x)=L(x)/(\underset{c}{\max }{L}^c(x)+\epsilon )$

使用$\hat{T}(x)\leftarrow \underset{c\in \left\{R,G,B\right\}}{\max }{L}^c(x)$去评估 illumination map $\hat{T} $. 使用计算目标像素周围小区域内相邻像素，

$\hat{T}(x)\leftarrow \underset{y\in \Omega (x)}{\max }\underset{c\in \left\{R,G,B\right\}}{\max }{L}^c(y)$

$\hat{T}(x)\leftarrow \underset{y\in \Omega (x)}{\mathrm{mean}}\underset{c\in \left\{R,G,B\right\}}{\max }{L}^c(y)$

$\Omega$ 是以像素$x$为中心的区域。$y$是区域内的位置索引。

保持整体结构和平滑的纹理细节，提出了$\underset{T}{\min }||\hat{T}-T|{|}_F^2+a||W\circ \Delta T|{|}_1$

B Exact Solver to Problem

T sub-problem

将$L=||T^{\prime }-T|{|}_F^2+k||W\cdot G|{|}_1+\Phi ((Z,\nabla T-G)$中$T$单独优化为 $T^{(t+1)}\leftarrow \underset{T}{\mathrm{argmin}}||\hat{T}-T|{|}_F^2\Phi ((Z^{(t)},\nabla T-G^{(t)})$,并对其求微分，令其为0：

$2(T-\hat{T})+{\mu }^{(t)}{D}^T(DT-G^{(t)})+D^T{Z}^{(t)}=0\Rightarrow (2I+{\mu }^{(t)}{D}^{T}D)T=2\hat{T}+{\mu }^{(t)}{D}^T(G^{(t)}-\frac{Z^{(t)}}{{\mu }^{(t)}})$

$I$为单位矩阵，D为具有向前差异的离散梯度算子的托普兹矩阵。通过快速傅里叶变换：

G sub-problem

去掉$L=||T^{\prime }-T|{|}_F^2+k||W\cdot G|{|}_1+\Phi ((Z,\nabla T-G)$中与G无关的项：

使用收缩操作获得：

Z and $\mu$

更新Z和$\mu $得到

C Sped-up Solver to Problem

进一步优化，迭代过程的因素是稀疏加权梯度项$||W\circ \Delta T|{|}_1$，$L1$正则项与在$T$上求梯度的运算。

(16)近似于$||W\circ \nabla T||$。因此$\underset{T}{\min }||\hat{T}-T|{|}_F^2+a||W\circ \Delta T|{|}_1$可得

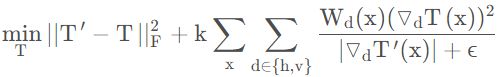
EXPERIMENTS

5 CONCLUSION

提出结构感知平滑模型。

设计两个算法：1.可以得到目标问题的精确最优解。2.节省大量时间的情况下求解近似问题

模型适用不同的加权策略。