非线性回归-最小二乘法

最小二乘法

在常规预测分析过程中如果预测的变量是连续的，最为常用的预测方式为回归分析，具体包括线性、非线性2类，其核心是采用最小二乘法（直线到各点的距离之和最小）对已知的样本数据进行最优拟合，然后通过拟合出的线性回归方程进行预测。其中线性回归模型分析的线性关系只是经济变量关系中的特例，在社会现实经济生活中很多现象之间会呈现非线性回归关系。以下是基于最小二乘法进行预测分析。

---

---

一、自定义数据

1.定义误差函数

首先先定义误差函数。

#t为需要拟合的参数
def residual(t, x, y):
    return y - (t[0] * x ** 2 + t[1] * x + t[2])

2.最小二乘拟合

x = np.array([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17])#运行年份
y = np.array([35173.67,30537.11,30082.01,31050.54,31542.88,39142.53,32279.91,32073.95,
              29001.95,32608.04,38033.41,32109.05,34993.80,40607.88,42412.81,53297.72786,
              57931.84])#对应各年份成本
p = optimize.leastsq(residual, [0, 0, 0], args=(x, y))#把residual函数中除了[0, 0, 0]以外的参数打包到args中
#leastsq(func, x0, args=()) func 是我们自己定义的一个计算误差的函数即residual,args 是指定func的其他参数，调用leastsq进行数据拟合, residual为计算误差的函数,
#x0为拟合参数的初始值,# args为需要拟合的实验数据这里将 (x,y)传递给args参数。Leastsq()会将这两个额外的参数传递给residual()。因此residual()有三个参数，t是拟合函数的参数，y和x是表示实验数据的数组
#关于leastsq()的说明：
#scipy.optimize.leastsq(func, x0, args=(), Dfun=None, full_output=0, col_deriv=0, ftol=1.49012e-08, xtol=1.49012e-08, gtol=0.0, maxfev=0, epsfcn=None, factor=100, diag=None)
#   参数：
#   （1）func：callable
#         应该至少接受一个(可能为N个向量)长度的参数，并返回M个浮点数。它不能返回NaN，否则拟合可能会失败。
#       func 是我们自己定义的一个计算误差的函数。
#  （2）x0：ndarray
#    x0 是计算的初始参数值。
#   （3）args：tuple, 可选参数
#         函数的所有其他参数都放在此元组中。
#      args 是指定func的其他参数。
#      一般我们只要指定前三个参数就可以了。
#   （4）Dfun：callable, 可选参数
#         一种计算函数的雅可比行列的函数或方法，其中行之间具有导数。如果为None，则将估算雅可比行列式。
#   （5）full_output：bool, 可选参数
#         非零可返回所有可选输出。
#   （6）col_deriv：bool, 可选参数
#         非零，以指定Jacobian函数在列下计算导数(速度更快，因为没有转置操作)。
#   （7）ftol：float, 可选参数
#         期望的相对误差平方和。
#   （8）xtol：float, 可选参数
#         近似解中需要的相对误差。
#   （9）gtol：float, 可选参数
#         函数向量和雅可比行列之间需要正交。
#   （10）maxfev：int, 可选参数
#        该函数的最大调用次数。如果提供了Dfun，则默认maxfev为100 *(N + 1)，其中N是x0中的元素数，否则默认maxfev为200 *(N + 1)。
#  （11）epsfcn：float, 可选参数
#        用于确定合适的步长以进行雅可比行进的正向差分近似的变量(对于Dfun = None)。通常，实际步长为sqrt(epsfcn)* x如果epsfcn小于机器精度，则假定相对误差约为机器精度。
#   （12）factor：float, 可选参数
#         决定初始步骤界限的参数(factor * || diag * x||)。应该间隔(0.1, 100)。
#   （13）diag：sequence, 可选参数
#         N个正条目，作为变量的比例因子。
#   返回值：
#   （1）x：ndarray
#         解决方案(或调用失败的最后一次迭代的结果)。
#   （2）cov_x：ndarray
#         黑森州的逆。 fjac和ipvt用于构造粗麻布的估计值。无值表示奇异矩阵，这意味着参数x的曲率在数值上是平坦的。要获得参数x的协方差矩阵，必须将cov_x乘以残差的方差-参见curve_fit。
#   （3）infodict：字典
#         带有键的可选输出字典：
#   （4）nfev
#         函数调用次数
#   （5）fvec
#         在输出处评估的函数
#   （6）fjac
#         最终近似雅可比矩阵的QR因式分解的R矩阵的排列，按列存储。与ipvt一起，可以估算出估计值的协方差。
#   （7）ipvt
#         长度为N的整数数组，它定义一个置换矩阵p，以使fjac * p = q * r，其中r是上三角形，其对角线元素的幅度没有增加。 p的第j列是单位矩阵的ipvt(j)列。
#   （8）qtf
#         向量(transpose(q)* fvec)。
#   （9）mesg：力量
#         字符串消息，提供有关失败原因的信息。
#   （10）ier：整型
#        整数标志。如果等于1、2、3或4，则找到解。否则，找不到解决方案。无论哪种情况，可选输出变量‘mesg’都会提供更多信息。

3.将拟合出来的参数赋值

#将拟合出来的参数赋值给theta
#theta中返回出来的值分别为回归公式y=axx+bx+c中的a、b、c值，最终预算公式替换值后为y=202.608xx-2500.12x+37867.189，x为对应的运行年限，y为估算的成本值。

theta = p[0] 
#预测趋势向前周期（根据预估周期往前推算运行年限，此处是从运行17年开始推算3年到运行20年）
x_hat = np.array([18,19,20])
y_hat = [(theta[0] * t ** 2 + theta[1] * t + theta[2]) for t in x_hat]
#“输出值”为预估运行18年、19年、20年的成本数据。
print("输出值:{}".format(y_hat))
#将预测值也表现在图中，重新给x,y赋值
x = np.append(x,x_hat)
y = np.append(y,y_hat)
#用2次多项式拟合x，y数组，其中x,y为坐标，2为阶数
a=np.polyfit(x,y,2)
#拟合完之后用这个函数来生成多项式对象
b=np.poly1d(a)
#生成多项式对象之后，就是获取x在这个多项式处的值
c=b(x)
# 设置画布大小，这行代码可放大弹出来的窗口大小，数值可随意设置
plt.figure(figsize=(20, 11))
#对原始数据画散点图
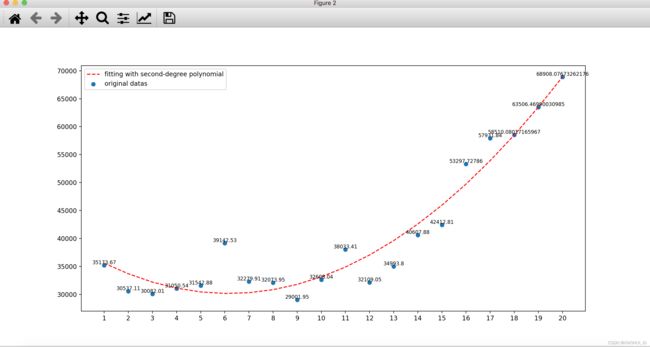
plt.scatter(x,y,marker='o',label='original datas')
#对拟合之后的数据，也就是x，c数组画图
plt.plot(x,c,ls='--',c='red',label='fitting with second-degree polynomial')
# 设置数字标签
for a, b in zip(x, y):
    plt.text(a, b, b, ha='center', va='bottom', fontsize=8)
#设置x轴的刻度
plt.xticks(x)
#函数主要的作用就是给图加上图例，plt.legend([x,y,z])里面的参数使用的是list的的形式将图表的的名称喂给这和函数
plt.legend()
#plt.legend( )中有handles、labels和loc三个参数，其中：
#handles需要传入你所画线条的实例对象
#labels是图例的名称（能够覆盖在plt.plot( )中label参数值）
#loc代表了图例在整个坐标轴平面中的位置（一般选取'best'这个参数值）

plt.show()

4.运行结果

二、数据库取值

import scipy.optimize as optimize
import matplotlib.pyplot as plt
import pymysql
import numpy as np

# 打开数据库连接
db = pymysql.connect(host='localhost',
                     user='root',
                     password='Aa1234567.',
                     database='testdb')
 
# 使用 cursor() 方法创建一个游标对象 cursor
cursor = db.cursor()
# SQL 查询语句
def residual(t, x, y):
    return y - (t[0] * x ** 2 + t[1] * x + t[2])

sql = "SELECT * FROM EMPLOYEE "
try:
   x = np.array([])
   y = np.array([])
   # 执行SQL语句
   cursor.execute(sql)
   # 获取所有记录列表
   results = cursor.fetchall()
   for row in results:
      date_date = row[0]
      rongliang = row[1]
      x = np.append(x,[date_date])
      y = np.append(y,[rongliang])
   #把residual函数中除了[0, 0, 0]以外的参数打包到args中
   p = optimize.leastsq(residual, [0, 0, 0], args=(x, y))
   theta = p[0] #将拟合出来的参数赋值给theta
   thetasss = p[1] 
   #测试值： (array([  202.60855183, -2500.12668909, 37867.18978211]), 1)

   #theta中返回出来的值分别为回归公式y=axx+bx+c中的a、b、c值，最终预算公式替换值后为y=202.608xx-2500.12x+37867.189，x为对应的运行年限，y为估算的成本值。

#预测趋势向前周期（根据预估周期往前推算运行年限，此处是从运行17年开始推算3年到运行20年）
   x_hat = np.array([18,19,20])
   y_hat = [(theta[0] * t ** 2 + theta[1] * t + theta[2]) for t in x_hat]
      #“输出值”为预估运行18年、19年、20年的成本数据。
   print("输出值:{}".format(y_hat))

#将预测值也表现在图中，重新给x,y赋值
   x = np.append(x,x_hat)
   y = np.append(y,y_hat)
   a=np.polyfit(x,y,2)#用2次多项式拟合x，y数组，其中x,y为坐标，2为阶数
   b=np.poly1d(a)#拟合完之后用这个函数来生成多项式对象
   c=b(x)#生成多项式对象之后，就是获取x在这个多项式处的值

   # 设置画布大小
   plt.figure(figsize=(20, 11))
   plt.scatter(x,y,marker='o',label='original datas')#对原始数据画散点图
   plt.plot(x,c,ls='--',c='red',label='fitting with second-degree polynomial')#对拟合之后的数据，也就是x，c数组画图
   #plt.plot(x,c, label='weight changes', linewidth=1, color='r', marker='o',
   #         markerfacecolor='blue', markersize=2)
   # 设置数字标签
   for a, b in zip(x, y):
       plt.text(a, b, b, ha='center', va='bottom', fontsize=8)

   #设置x轴的刻度
   plt.xticks(x)
   plt.legend()#函数主要的作用就是给图加上图例，plt.legend([x,y,z])里面的参数使用的是list的的形式将图表的的名称喂给这和函数
   #plt.legend( )中有handles、labels和loc三个参数，其中：
   #handles需要传入你所画线条的实例对象
   #labels是图例的名称（能够覆盖在plt.plot( )中label参数值）
   #loc代表了图例在整个坐标轴平面中的位置（一般选取'best'这个参数值）

   plt.show()
except:
   print ("Error: unable to fetch data")
# 关闭数据库连接

db.close()

---

总结

又学习了新知识，继续努力。