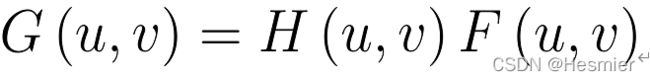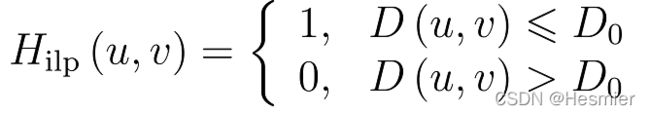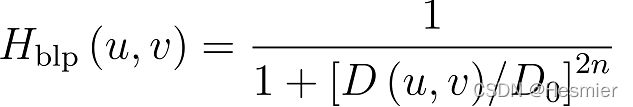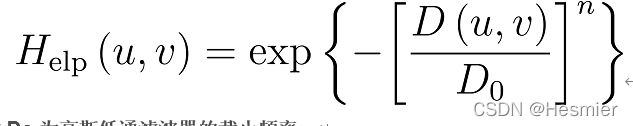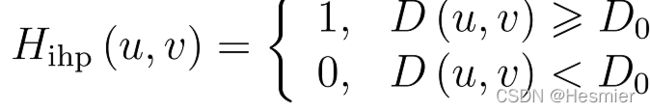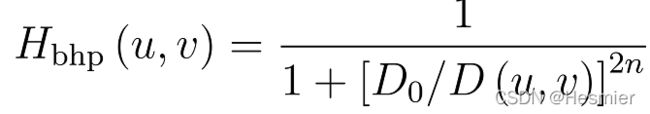数字图像处理 实验二
环境:windows11 matlab2018b
实验中有借鉴部分,请注意!!!
一、实验目的:
- 掌握傅里叶变换及逆变换的基本原理方法。
- 理解频域滤波的基本原理及方法。
- 掌握进行图像的频域滤波的方法。
二、实验原理:
1.平滑空域滤波:
一般分为两种,一种是线性平滑滤波器,一种值非线性平滑滤波器。
平滑滤波器主要有以下几种用途:
①对大图像处理前,删去无用的细小细节;②连接中断的线段和曲线;
③降低噪音;④平滑处理,恢复过分锐化的图像;⑤图像创意(阴影、软边、朦胧效果)。
(1).线性就是对观察结果进行线性组合,线性滤波做的所有事情就是实现乘积求和操作。线性低通平滑滤波器的所有系数都是正数,对3*3的模板来说,最简均值滤波器的是取所有系数为1,为了保持输出图像仍然在原图像的灰度值范围内,模板与像素邻域的乘积都要除以9。
(2).而非线性就是作用在一组观察结果上并产生对未观察量的估计,它是对观察结果的逻辑组合。不能表示成乘积和形式的滤波器就是非线性滤波。
其滤波原理与均值滤波器方法类似,但不是计算加权求和,而是把邻域中的图像的像素按灰度级进行排序,然后选择该组的中间值作为输出像素值。
2. 锐化滤波器
图像平滑往往使图像中的边界、轮廓变得模糊,为了减少这类不利效果的影响,需要利用图像锐化技术,使图像的边缘变得清晰。
(1).利用对应微分的方法可以对图像进行锐化滤波
线性锐化滤波器也可用模板卷积来实现,仅中心系数为正,而周围系数均为负值(或相反)
(2).matlab中常见的非线性滤波器是最小值滤波器、最大值滤波器和中值滤波器。
3. 频域增强
频域增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其他空间中,然后利用该空间的特有性质方便地进行图像处理,最后再转换回原来的图像空间中,从而得到处理后的图像。
在频域中,变换系数反映了某些图像的特征。如频谱的直流分量比例于图像的平均亮度、噪音对应于频率较高的区域、图像实体对应于频率较低的区域
在频谱中,图像中心处对应了图像中变化较平缓的区域,四周对应了图像边缘、噪音或者变化陡峭的部分。因此我们可以将代表了图像边缘、噪音或者变化陡峭的高频率成分滤除掉,只留下变化平缓的低频率成分,再由频域变换回时域,这就相当于对图像进行了平滑处理;相反,若滤去低频率成分,只留下高频率成分,就相当于对图像进行了锐化处理。
4.低通滤波:
低通滤波器的作用是消除图像中的高频部分,使图像变得更加平滑。
低通滤波表达式;
理想低通滤波器(ILPF)
其中Do为理想低通滤波器的截止频率。理想低通滤波器具有平滑图像的作用,但是有很严重的振铃现象。
巴特沃斯低通滤波器(BLPF)
其中Do为巴特沃斯低通滤波器的截止频率,参数n为巴特沃斯滤波器的阶数,n越大则滤波器的形状越陡峭。
指数型低通滤波器(ELPF)
其中Do为高斯低通滤波器的截止频率。
低通滤波也分为理想低通滤波、布特沃斯低通滤波、高斯低通滤波等。
5.高通滤波:
高通滤波与低通滤波相反,它是高频分量顺利通过,使低频分量受到削弱。
理想高通滤波器(IHPF)
巴特沃斯高通滤波器(BLPF)
指数型高通滤波器(ELPF)
三、实验内容步骤
要求使用MATLAB或OpenCV来完成以下实验。
1.平滑空域滤波
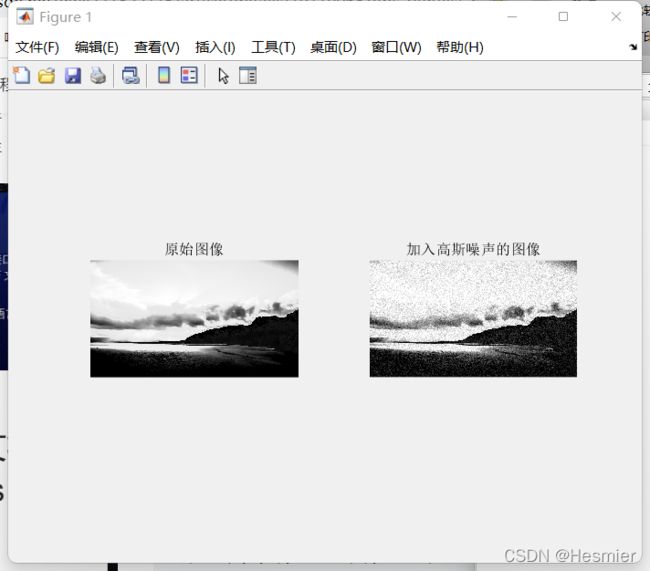
1).读出一幅灰度图像,给这幅图像分别加入椒盐噪声和高斯噪声后并与前一张图显示在同一图像窗口中。
2).对加入噪声图像选用不同的平滑(低通)模板做运算,对比不同模板所形成的效果,要求在同一窗口中显示。
3).如果使用MATLAB,使用函数imfilter时,分别采用不同的填充方法(或边界选项,如零填充、’replicate’、’symmetric’、’circular’)进行低通滤波,显示处理后的图像。
4).运用for循环,将加有椒盐噪声的图像进行10次、20次均值滤波,查看其特点,显示均值处理后的图像(提示:利用fspecial函数的’average’类型生成均值滤波器)。
5).对加入椒盐噪声的图像分别采用均值滤波法,和中值滤波法对有噪声的图像做处理,要求在同一窗口中显示结果。
6).自己设计平滑空间滤波器,并将其对噪声图像进行处理,显示处理后的图像。
2.锐化空域滤波:
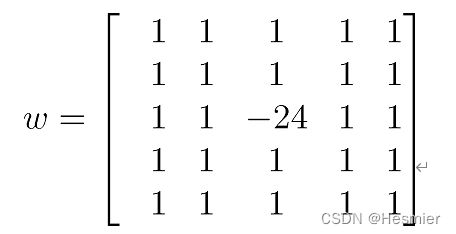
1).读出一幅灰度图像,采用3*3的拉普拉斯算子w=[1,1,1;1,-8,1;1,1,1]对其进行滤波。
2).编写函数w = genlaplacian(n),自动产生任一奇数尺寸n的拉普拉斯算子,
3).分别采用3*3、9*9、15*15、25*25大小的拉普拉斯算子对图像进行锐化滤波,并利用式
采用不同的梯度算子对图像进行锐化滤波,并比较其效果。
4).自己设计锐化空间滤波器,并将其对噪声图像进行处理,显示处理后的图像。
3.傅里叶变化:
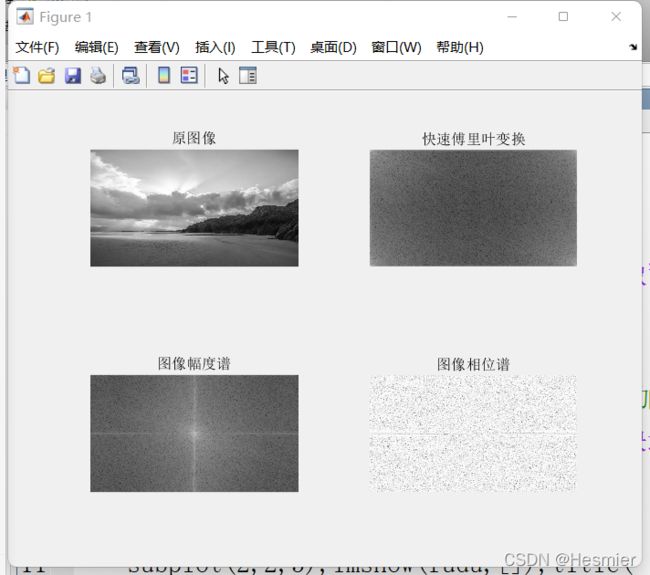
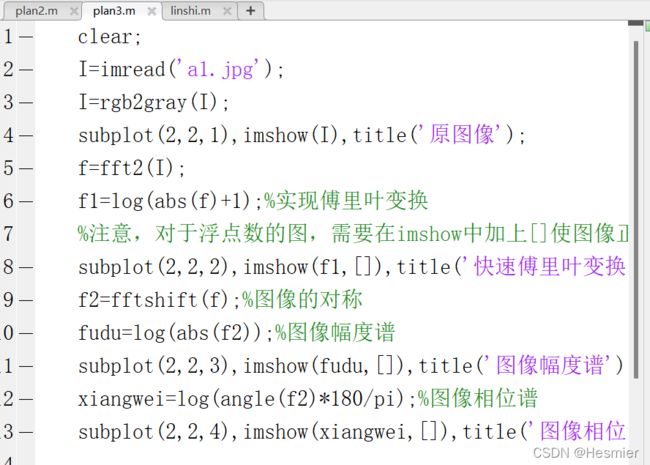
1).读出一幅灰度图像,对其进行快速傅里叶变换,分别显示其幅度图像和相位图像。
2).仅对相位部分进行傅里叶逆变换后查看结果图像。
3).仅对幅度部分进行傅里叶逆变换后查看结果图像。
4).将图像的傅里叶变换置为其共轭后进行逆变换,比较新生成图像与原始图像的差异。
4.平滑频域滤波:
1).设计理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器,截止频率自选。
2).读出一幅灰度图像,分别采用理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器对其进行滤波(截止频率自选),再做逆变换,观察不同的截止频率下采用不同低通滤波器得到的图像与原图像的区别,特别注意振铃效应。
5.锐化频域滤波:
1).设计理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器,截止频率自选。
2).读出一幅灰度图像,分别采用理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器对其进行滤波(截止频率自选),再做逆变换,观察不同的截止频率下采用不同高通滤波器得到的图像与原图像的区别。
实验开始:
1.平滑空域滤波:
(1)首先加入两个噪声,这里使用了imnosie函数进行加入
加入椒盐噪声:
加入高斯噪声:
(2)进行平滑模板处理
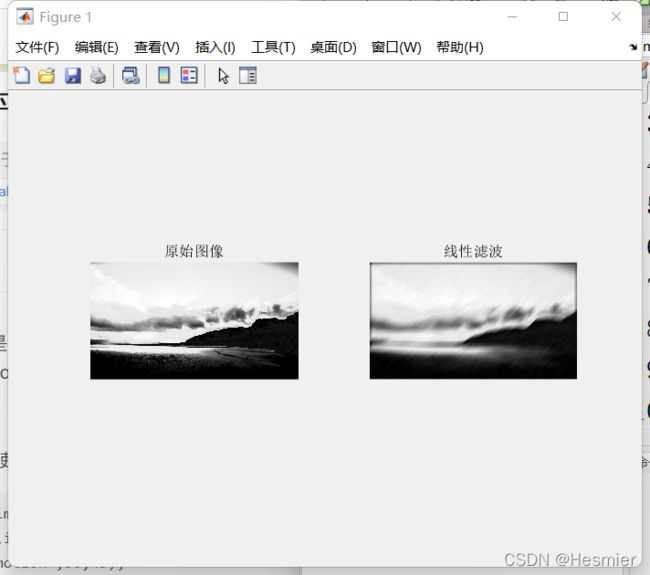
1.线性滤波:
2.中值滤波:
3.自适应滤波:
对比了三张图片,发现自适应滤波的平滑效果是最好的,线性滤波的平滑效果个人感觉是最差的,中值滤波的效果一般。
(3)图像的填充:
1.零填充:
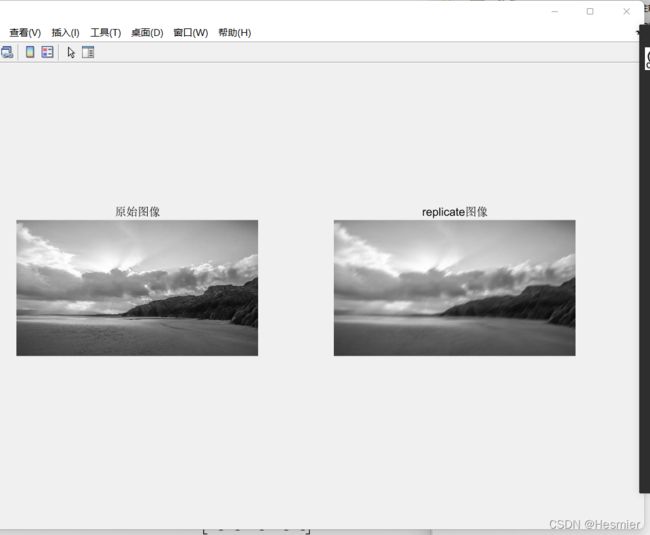
2.’replicate’填充:
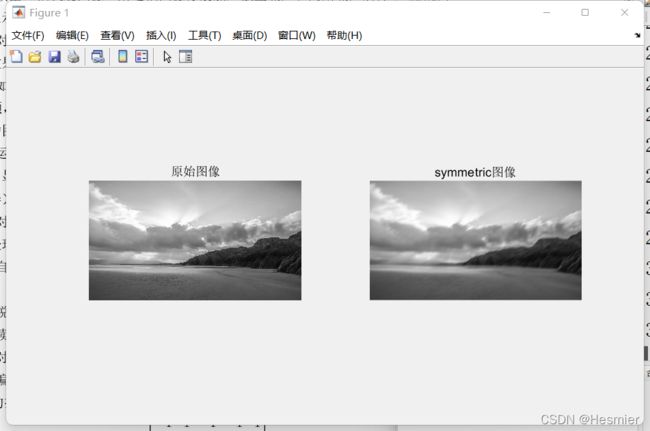
3.’symmetric’填充:
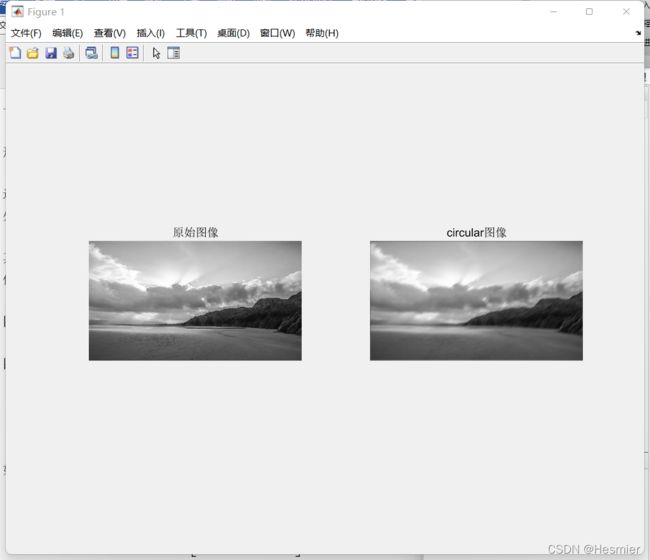
4.‘circular’填充:
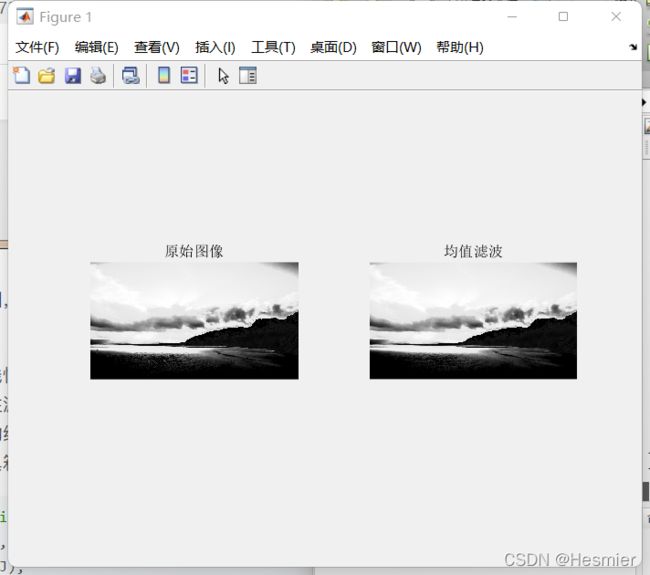
(4).循环均值滤波:
1.循环10次后的图像:
2.循环20次后的图像:
(5).处理:
1.椒盐后进行均值滤波法:
2.椒盐后进行中值滤波法:
(6)设计平滑滤波器:
2.锐化空域滤波:
(1)拉普拉斯算子滤波:
(2)编写函数自动产生拉普拉斯算子:
(3)采用不同的拉普拉斯算子对图像进行处理:
首先是锐化函数:
然后是拉普拉斯处理:
5*5的拉普拉斯算子处理和增强:
9*9拉普拉斯算子:
15*15拉普拉斯算子:
25*25拉普拉斯算子:
通过观察,锐化增强之后的图像会比原图像增加多个白点或者黑点。增强之后的图像感觉不会比原图像清晰。
(4)
梯度算子:
(5).设计空间滤波器:
但是这个设计对处理噪声效果不好。
3.傅里叶变换:
(1).
(2).相位部分傅里叶变换:
(3):
幅度部分傅里叶逆变换:
(4)将图像共轭后逆变换:
新生成的图像相较于原图像是旋转了90度并且对称过了的,同时,生成的图像有图像描边的轮廓。
4.(1).理想低通滤波器:
布特沃斯低通滤波器:
高斯低通滤波器:
高斯滤波器的截止频率也选择了100
(2)
之前先贴上逆变换的代码:
然后查看每个变换的结果。
理想滤波低通变换:
布特沃斯低通变换:
高斯低通滤波变换:
经过滤波后发现,理想滤波之后的图像会比之前的图像模糊,图像上会多出几条竖波痕,原本发亮的太阳部分亮度会衰弱。
布特沃斯滤波之后的图像也是变得模糊,但是亮光部分比理想滤波更亮,对于图像来说,更加显示图形的平滑。
高斯滤波之后的图像在亮度方面感觉会比前两个滤波更加好,图像的暗处似乎会比前两个滤波更加暗一些,图像整体的平滑会比布特沃斯滤波更好一些。
5.这里所有的滤波器的截止频率全部选择100.
(1).理想滤高通波器:
这里的代码与低通滤波器其实很相像,只是将小于号改成了大于号:
布特沃斯高通滤波器:
也是代码改动的地方较小:
将原来的 d,/d0 改成 d0./d,同时去掉了mat2gray:
高斯高通滤波:
也是将原来的代码部分进行改变:
原来的 exp((-d.^2)/(2*(d0).^2)) 改成前面加上1减
(2)不同滤波的图像结果:
理想高通滤波:
布特沃斯高通滤波:
高斯高通滤波:
![]()
经过观察,理想高通滤波图像中的白线相对来说还算明显,同时,白线的连续性还不错。
布沃斯特高通滤波处理之后的图像白线几乎看不见,更多的是白点的出现,而且这些白点也是不连续的。
高斯高通滤波处理之后的图像有白线也有白点,不过白点与白线都是不连续的,而且白点和白线都是颜色比较淡的。