数据挖掘BUC算法计算冰山立方体的python实现
冰山立方体计算
在很多情况下,数据立方体的空间大多被低度量值的数据单元所占据,而这些数据单元往往是分析者很少关心的内容。冰山立方体的计算能够减少物化数据单元所占有的存储空间。
常用计算方法:
BUC:Bottom-Up Computation
Star-Cubing
MMCubing,C-Cubing等
下面,我将就BUC算法的原理及实现做具体介绍:
BUC主要思想:
buc是一种从顶点立方体逐步向下到基本立方体的计算方法,用于计算稀疏冰山立方体。首先计算整个数据立方体的度量值,然后沿着每个维度进行划分,同时检查冰山条件,对不满足条件的分枝进行剪枝操作,对满足的在下一个维度讲行递归搜索。
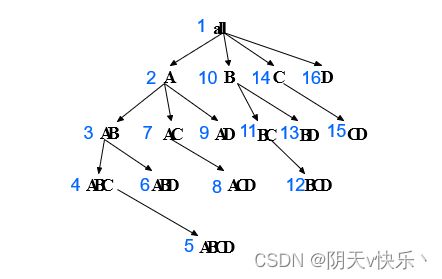
BUC计算流程:
- 首先,扫描整个输入,计算整个度量(如总计数);
- 针对方体的每一维进行划分 ;
- 针对每一个划分,对它进行聚集,为该划分创建一个元组并得到该元组的计数。判断其分组计数是否满足最小支持度;
- 如果满足,输出该划分的聚集元组,并在该划分上对下一维进行递归调用,否则进行剪枝操作。
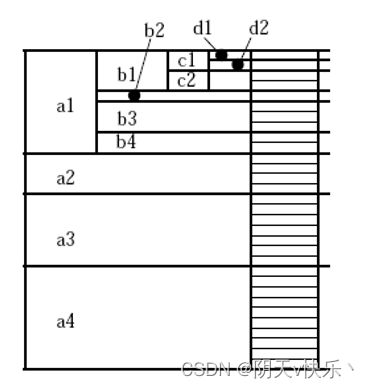
BUC算法特点及缺陷:
- BUC算法中采用了分治策略,优点在于能够分担划分开销,减少不必要的计算消耗。
- BUC的性能容易受到维的次序以及不平衡数据的影响,应当以维基数的递减顺序进行划分。
- BUC不像多路数组聚集(MultiWay),不能利用父子关系共享聚集计算。
BUC的算法实现:
首先我引入自定义数据集,BUC-test2.csv:
a1 b1 c1 d1
a1 b1 c2 d2
a1 b1 c2 d2
a2 b1 c1 d2
a2 b2 c2 d2
a3 b3 c1 d1
a4 b4 c1 d1
import pandas as pd
dataList = pd.read_csv('BUC-test2.csv') #读取数据集
print(dataList)
print("维数:",dataList.columns.size) #统计数据的维数
lenN = dataList.columns.size
NumFall = [0] * lenN # [0, 0, 0, 0]
ValueFAll = [] # [[a1,a2....],[b1,b2...]],定义一个列表value0fall用来统计并存储各维不重复的叶结点。
for j in range(lenN):
ValueSingle = [] # 单个维度的取值
for i in range(len(dataList)):
if dataList.iloc[i, j] not in ValueSingle: #通过行号选取数据判断在不在列表ValueFall中
ValueSingle.append(dataList.iloc[i, j])
ValueFAll.append(ValueSingle)
NumFall[j] = len(ValueSingle)
# 逐列逐行进行遍历,将每一列出现的非重复元素,加入到ValueSingle中,并统计个数,放到NumFall中
print("ValueFAll:",ValueFAll)
print("NumFall:",NumFall)
print("BUC:")
# 计算(temp)list出现次数:
def count(list, data):
number = 0
for i in range(len(data)):
isIn = True
for j in range(len(list)):
if list[j] not in data.iloc[i].tolist(): # 将series对象转list才能not in
isIn = False
break
if isIn:
number = number + 1
return number
def BUC(tempList, n, curN, min_sup=3): # curN代表当前维度游标,最小支持度设为3
if curN == n:
return # 退出递归
for i in range(NumFall[curN]):
tempList.append(ValueFAll[curN][i])
if count(tempList, dataList) >= min_sup:
print("%s :%d" % (str(tempList), count(tempList, dataList)))
BUC(tempList, n, curN + 1) # 加一维度递归调用
tempList.pop()
BUC(tempList, n, curN + 1)
BUC([], 4, 0)
程序的输出为:
维数: 4
ValueFAll: [['a1', 'a2', 'a3', 'a4'], ['b1', 'b2', 'b3', 'b4'], ['c1', 'c2'], ['d1', 'd2']]
NumFall: [4, 4, 2, 2]
BUC:
['a1'] :3
['a1', 'b1'] :3
['b1'] :4
['b1', 'd2'] :3
['c1'] :4
['c1', 'd1'] :3
['c2'] :3
['c2', 'd2'] :3
['d1'] :3
['d2'] :4
总结:
BUC算法首先将拿到的数据进行维的划分,再对每个维进行属性的划分。例如,本实例首先将数据划分为A、B、C、D四个维度,而每个维度的划分依次为:[[‘a1’, ‘a2’, ‘a3’, ‘a4’], [‘b1’, ‘b2’, ‘b3’, ‘b4’], [‘c1’, ‘c2’], [‘d1’, ‘d2’]]。BUC算法的特点是用到了函数的递归调用,将每一个根节点的所有符合冰山条件(满足最小阈值)的子树输出,将不符合条件的子树进行剪枝操作。