NNDL 作业4：第四章课后题

目录

4-2 试设计一个前馈神经网络来解决XOR问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用ReLUctant作为激活函数。

4-3 试举例说明“死亡ReLU问题”，并提出解决方法。

4-7 为什么在神经网络模型的结构化风险函数中不对偏置 b 进行正则化？

4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 W=0,b=0 ？

4-9 梯度消失问题是否可以通过增加学习率来缓解？

---

4-2 试设计一个前馈神经网络来解决XOR问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用ReLUctant作为激活函数。

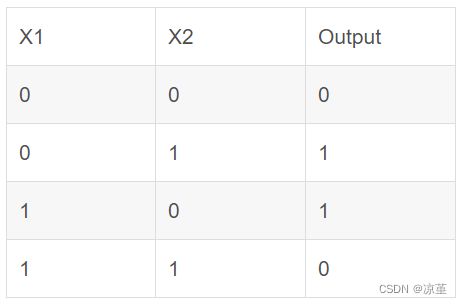
XOR问题：

 由图可知，(0,0)、(0,1)、(1,0)、(1,1)对应的标签分别是是0、1、1、0。

XOR输入为2个神经元，输出为一个神经元，此题要求隐藏神经元为2个，故只要两层全连接层即可。

代码如下：

import torch.nn as nn
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
import math
import numpy as np
 
from torch.autograd import Variable
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_

# 异或门模块由两个全连接层构成
class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(normal_(w1,mean=0.0, std=1.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(normal_(w2,mean=0.0, std=1.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = nn.ReLU()
 
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2


# 输入和输出数据
input_x = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
input_x1 = input_x.float()
real_y = torch.Tensor([[0], [1], [1], [0]])
real_y1 = real_y.float()
# 设置损失函数和参数优化函数
net = Model_MLP_L2_V2(2,2,1)
loss_function = nn.MSELoss(reduction='mean')  # 用交叉熵损失函数会出现维度错误
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)  # 用Adam优化参数选不好会出现计算值超出0-1的范围
epochs=2000   #训练次数

# 进行训练
for epoch in range(epochs):
    out_y = net(input_x1)
    loss = loss_function(out_y, real_y1)  # 计算损失函数
    # print('啦啦啦')
    optimizer.zero_grad()  # 对梯度清零，避免造成累加
    loss.backward()  # 反向传播
    optimizer.step()  # 参数更新

# 打印计算的权值和偏置
print('w1 = ', net.fc1.weight.detach().numpy())
print('b1 = ', net.fc1.bias.detach().numpy())
print('w2 = ', net.fc2.weight.detach().numpy())
print('b2 = ', net.fc2.bias.detach().numpy())
input_test = input_x1
out_test = net(input_test)
print('input_x', input_test.detach().numpy())
print('out_y', out_test.detach().numpy())

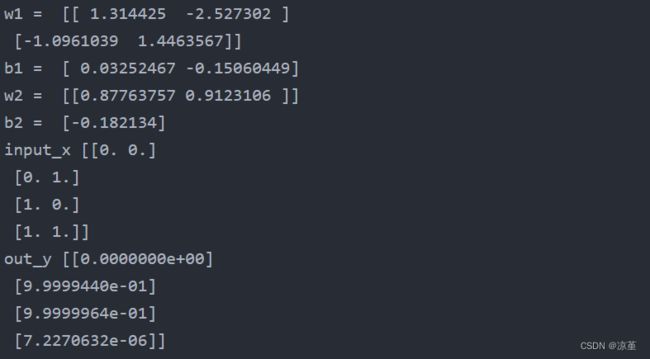
运行结果：

4-3 试举例说明“死亡ReLU问题”，并提出解决方法。

 

“死亡ReLU问题”是指参数再一次不恰当的更新后，使得隐藏层神经元的输入全部为负数，ReLU函数无法对其激活，那么神经元自身参数的梯度永远都是0，以后的训练过程中永远都不会被激活。

以二分类为例，设 y, 分别表示单个样本的真实标签和预测结果。

则交叉熵损失函数为: loss(y,)=−(ylog+(1−y)log(1−)) 。 

y,都为1时， loss=−log1=0 ； 

y,分别为1,0时， loss=+∞ ；

 y,分别为0,1时， loss=−∞ ；

 y, 都为0时， loss=0 。

由此可知要想使损失尽可能小，则 y 为1时，  要尽可能大； y 为0时， 要尽可能小。所以在后者情况下，就要使 w 尽可能小。若稍有不慎，在某个节点上所有样本的输出全部为负数，因而梯度为0，因而此处权重无法更新，因而成了死亡节点。

因而想要尽量避免死亡节点，可以使得w在一次更新中变化的缓和或者函数在抑制区的导数不为0。可以使用L2正则化，或者其他的梯度下降方式如动能，RMS ,Adam等避免或使用带泄露的ReLU、带参数的ReLU、ELU函数以及Softplus函数，也可以学习率不要设置太大。 

4-7 为什么在神经网络模型的结构化风险函数中不对偏置 b 进行正则化？

正则化主要是为了防止过拟合，而过拟合一般表现为模型对于输入的微小改变产生了输出的较大差异，这主要是由于有些参数 w 过大的关系，通过对 ||w|| 进行惩罚，可以缓解这种问题。而如果对 ||b|| 进行惩罚，其实是没有作用的，因为在对输出结果的贡献中，参数b对于输入的改变是不敏感的，不管输入改变是大还是小，参数b的贡献就只是加个偏置而已。

或者说，模型对于输入的微小改变产生了输出的较大差异，这是因为模型的“曲率”太大，而模型的曲率是由 w 决定的， b 不贡献曲率（对输入进行求导， b 是直接约掉的）。

4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 W=0,b=0 ？

因为如果参数都设为0，在第一遍前向计算的过程中所有的隐藏层神经元的激活值都相同。在反向传播时，所有权重更新也都相同，这样会导致隐藏层神经元没有区分性。这种现象称为对称权重现象。

4-9 梯度消失问题是否可以通过增加学习率来缓解？

梯度消失：梯度趋近于零，网络权重无法更新或更新的很微小，网络训练再久也不会有效果，它本质上是由于深度神经网络的反向传播造成的，根本原因在于反向传播训练法则，属于先天不足。从图像来看，tanh比sigmoid的梯度值要高，不过值也是小于1的，两边也会出现饱和，也会引起梯度消失的现象。、

梯度消失问题不可以通过增加学习率来缓解，因为梯度消失不是指梯度太小，而是指梯度在最后一层往前传的过程中不断减小，这个消失，指的是最底层的梯度和最高层的梯度量级的差别。

如果增大了lr，底层的学习可能确实更加有效了，高层的梯度就可能炸了。

参考文献

https://blog.csdn.net/weixin_46470894/article/details/107145207

https://zhuanlan.zhihu.com/p/344110415

http://t.csdn.cn/Xc6gf