基于R语言的分位数回归（quantile regression）

分位数回归（quantile regression）
这一讲，我们谈谈分位数回归的知识，我想大家传统回归都经常见到。分位数回归可能大家见的少一些，其实这个方法也很早了，大概78年代就有了，但是那个时候这个理论还不完善。到2005年的时候，分位数回归的创立者Koenker R写了一本分位数回归的专著，剑桥大学出版社出版的。今年本来老爷子要出一本《handbook of quantile regression》，还没有正式出来呢，目前来看，分位数回归应用的范围非常广。在金融领域尤为重要。下面先给大家简单介绍一下，分位数回归的基本原理，完后拿R做一个完整的案例。为什么拿R软件，因为分位数回归的发明者最早拿R写了一个包，叫quantreag，是当时唯一一个分位数回归的包，现在的话，看到python，julia也有相关的包了。但是感觉这个R的还是最好的。
那么什么是分位数回归呢，这个就要从传统的回归说起，传统回归呢，一般叫最小二乘回归，也叫均值回归。这个均值是指条件均值。比较抽象，在前面有一篇博文中，我比较详细地解释过。那么分位数回归就是均值回归的拓展，也就是它可以拟合均值以外的其它分位点，形成多条回归线，这里首先需要强调的是分位数回归的分位点是指因变量y的分位点，不是x的。这样我们如果设定多个分位点就得到了多条回归直线。当然分位数回归现在也发展出来非线性分位数回归，就是可以拟合出多条曲线，或者和广义线性回归模型一样可以适用二值变量。要说分位数回归具体的原理，后面有空再细谈。下面我们拿R语言做一个案例，大家就可以逐渐感受到分位数回归具体的含义了。案例所用的数据呢，大家应该都比较熟悉，就是收入和食品消费支出的数据，下面看代码。

#导入分位数回归的包
library(quantreg)                         
# 引入数据
data(engel)
#查看数据格式
mode(engel)
[1] "list"
#查看变量名
names(engel)
[1] "income"  "foodexp"
#查看格式
class(engel)
[1] "data.frame"
#查看数据的前五行
head(engel)
income  foodexp
1 420.1577 255.8394
2 541.4117 310.9587
3 901.1575 485.6800
4 639.0802 402.9974
5 750.8756 495.5608
6 945.7989 633.7978
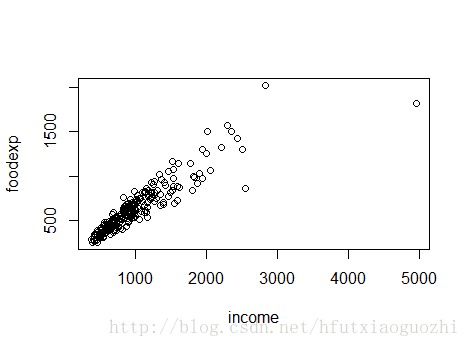
#画个散点图看看数据
plot(engel$income, engel$foodexp, xlab='income', ylab='foodexp')

图是这样的

下面我们继续简单查看一下数据

#查看foodexp的变化范围
boxplot(engel$foodexp, xlab='foodexp')
#简单验证一下因变量foodexp是否服从正态分布
qqnorm(engel$foodexp, main='QQ plot')
qqline(engel$foodexp, col='red', lwd=2)

结果如下：

下面是QQ图

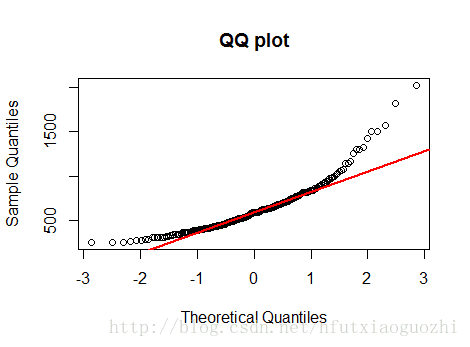
结果表明，因变量y明显不服从正态分布，但是呢，分位数回归不要求y服从正态分布，不仅如此，而且分位数回归还对异常值点不敏感。下面我们继续，为了对比，我们仍然做一个均值回归，再做一个分位数回归。

#可以直接调用数据框里变量
attach(engel)
#设置0.05, 0.25, 0.5, 0.75, 0.95五个分位点，并且进行分位数回归，这样可以得到五条分位数回归线
rq_result <- rq(foodexp ~ income, tau=c(0.05, 0.25, 0.5, 0.75, 0.95))
summary(rq_result)
Call: rq(formula = foodexp ~ income, tau = c(0.05, 0.25, 0.5, 0.75, 
    0.95))

tau: [1] 0.05

Coefficients:
            coefficients lower bd  upper bd 
(Intercept) 124.88004     98.30212 130.51695
income        0.34336      0.34333   0.38975

Call: rq(formula = foodexp ~ income, tau = c(0.05, 0.25, 0.5, 0.75, 
    0.95))

tau: [1] 0.25

Coefficients:
            coefficients lower bd  upper bd 
(Intercept)  95.48354     73.78608 120.09847
income        0.47410      0.42033   0.49433

Call: rq(formula = foodexp ~ income, tau = c(0.05, 0.25, 0.5, 0.75, 
    0.95))

tau: [1] 0.5

Coefficients:
            coefficients lower bd  upper bd 
(Intercept)  81.48225     53.25915 114.01156
income        0.56018      0.48702   0.60199

Call: rq(formula = foodexp ~ income, tau = c(0.05, 0.25, 0.5, 0.75, 
    0.95))

tau: [1] 0.75

Coefficients:
            coefficients lower bd  upper bd 
(Intercept)  62.39659     32.74488 107.31362
income        0.64401      0.58016   0.69041

Call: rq(formula = foodexp ~ income, tau = c(0.05, 0.25, 0.5, 0.75, 
    0.95))

tau: [1] 0.95

Coefficients:
            coefficients lower bd upper bd
(Intercept) 64.10396     46.26495 83.57896
income       0.70907      0.67390  0.73444
#上面就是没条回归线的回归系数，我们做个图看一下
plot(income, foodexp, cex=0.25, type='n', xlab='income', ylab='foodexp')
points(income, foodexp, cex=0.5, col='blue')
#加中位数数回归的直线
abline(rq(foodexp~income, tau=0.5), col='blue')
#加均值回归的五条直线
abline(lm(foodexp~income), lty=2, col='red')
#将分位数回归的五条线加上去
taus <- c(0.05, 0.1, 0.25, 0.75, 0.9, 0.95)
#
for (i in 1:length(taus)){
  abline(rq(foodexp~income, tau=taus[i]), col='gray')
}

效果如下：

从上图，我们可以看到，分位数回归可以拟合出多条直线，这个对于我们数据分布比较复杂的时候，很有用处，每条线反应了不同档次下，自变量与因变量的关系。实际上这个只是分位数回归的一小部分应用，得到不同分位点下的数据，我们还可以进行概率密度估计，得到相应的概率密度预测。
这一讲我们就到这。