机器学习学习笔记(二)---PR曲线
学习笔记 PR曲线
- 一、P和R代表什么
-
- TP FP TN FN 基本概念
- P与R 的定义
- 评估PR曲线
- 二、绘制PR曲线
-
- 代码
- 参考文献
一、P和R代表什么
在信息检索中,我们经常会关心“检索出的信息中有多少比例是用户感兴趣的”“用户感兴趣的信息中有多少被检索出来了”。“查准率”(precision)与“查全率”(recall)是更为适用于此类需求的性能度量。
查准率P亦称“准确率”
查全率R亦称“召回率”
TP FP TN FN 基本概念
对于二分类问题,可将样例根据其真实类别与学习器预测类别的组合划分为真正例(true positive)、假正例(false positive)、真反例(true negative)、假反例(false negative)四种情形,令TP、FP、TN、FN分别表示其对应的样例数,则显然有TP+FP+TN+FN=样例总数.分类结果的“混淆矩阵”(confusion matrix)如图所示.
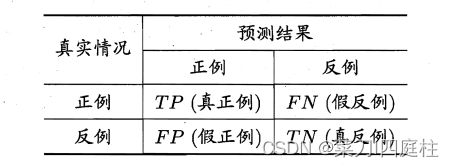
真正例(true positive) TP:预测结果为正例,真实结果也为正例。
假正例(false positive) FP:预测结果为正例,真实结果却为反例。
真反例(true negative) TN:预测结果为反例,真实结果也为反例。
假反例(false negative) FN:预测结果为反例,真实结果却为正例。
P与R 的定义
准确率P和召回率R分别定义为:

准确率和召回率是一对矛盾的度量,一般来说,准确率高时,召回率偏低;而召回率高时,准确率往往偏低。
(穷则精准打击,富则活力覆盖?!。。。)
根据机器学习的预测结果对样例进行排序,排在前面是学习机器认为可能性最高的正例,第二为次高,以此类推,直到最后是学习机器认为最不可能的正例样本。
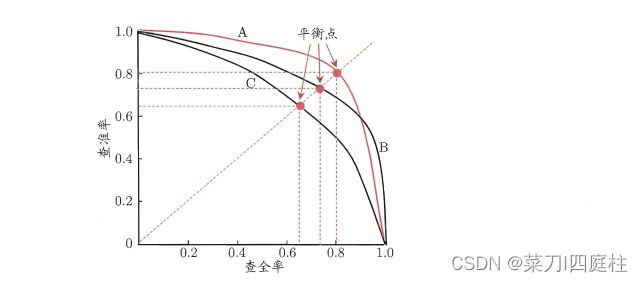
按此顺序逐个把样本作为正例进行预测,则每次可以计算出当前的查全率,查准率.以查准率为纵轴、查全率为横轴作图,就得到了查准率-查全率曲线,即“P-R曲线”。
评估PR曲线
一般认为,一个曲线完全"包住"另一个曲线,则认为前者性能优于后者;如果两个曲线发生了相交,则不能直接认为两者的优劣,只能在具体的条件下进行比较。一个合理的判据是比较P-R曲线下面积的大小。
“平衡点”(Break-Event Point,简称BEP)是一个综合考虑查准率,查全率的性能度量,它是二者相同时的取值。可以通过比较曲线间的BEP的值来粗略判断优劣(在不同的应用场景中,重视的程度有所不同)
由于BER过于简化,更常用的是F1度量:

F1度量的一般形式--------Fβ

其中β>0度量了查全率对查准率的相对重要性. β = 1时退化为标准的F1; β >1时查全率有更大影响;β<1时查准率有更大影响.
二、绘制PR曲线
首先我们需要一个阈值T,大于等于这个阈值的我们认为是正样例,小于这个阈值的认为是负样例。
通过设置t的数量n,可以得到n对P和R的值,以此来评判模型的好坏。
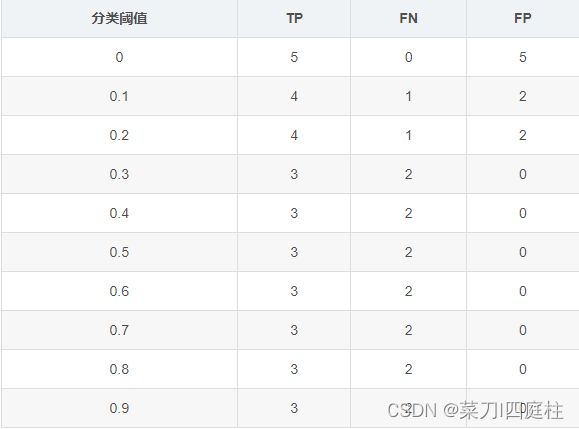
(假设我们有如下数据)
代码
import matplotlib.pyplot as plt
import numpy as np
if __name__=='__main__':
TP=np.array([5,4,4,3,3,3,3,3,3,3])
FN=np.array([0,1,1,2,2,2,2,2,2,2])
FP=np.array([5,2,2,0,0,0,0,0,0,0])
P=TP/(TP+FP)
R=TP/(TP+FN)
plt.plot(R, P)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()
参考文献
周志华的西瓜书—《机器学习》