机器学习-Chapter 02 监督学习（Python）
@参考Python机器学习基础教程
Chapter 02 监督学习
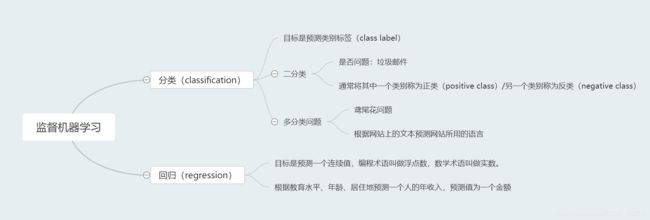
1. 分类与回归
监督机器学习问题主要有两种，分别叫做分类（classification）与回归（regression）。
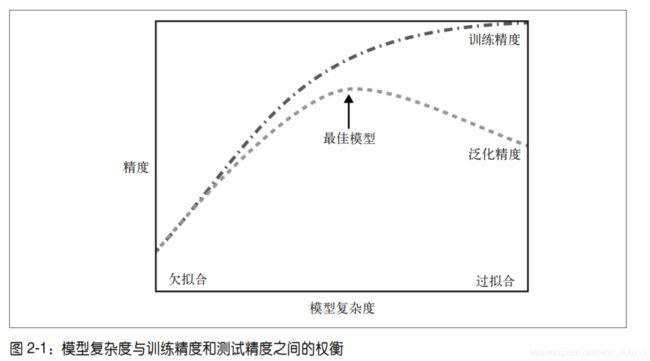
2. 泛化、过拟合与欠拟合
泛化：一个模型能够对没见过的数据做出准确预测，我们称之能够从训练集泛化到测试集。构建一个泛化精度尽可能高的模型
过拟合：使用非常精准的特征描述，对测试集非常准确预测，但对新的数据无法进行准确预测。
欠拟合：使用较少特征描述，同样对新的数据无法进行预测。
3. 监督学习算法
算法使用手册->链接：scikit-learn文档.
（1）一些样本数据集
二分类数据集实例-> forge数据集
X, y = mglearn.datasets.make_forge() #X和y是forge返回的两个特征
mglearn.discrete_scatter(X[:,0],X[:,1],y) #输入X第0列和第1列作为x轴，y轴
plt.legend(["Class 0","Class 1"],loc = 4) #设置图像的分类
plt.xlabel("First feature") #设置图像x轴名称
plt.ylabel("Second feature") #设置图像y轴名称
print("X.shape:{}".format(X.shape)) #返回数据
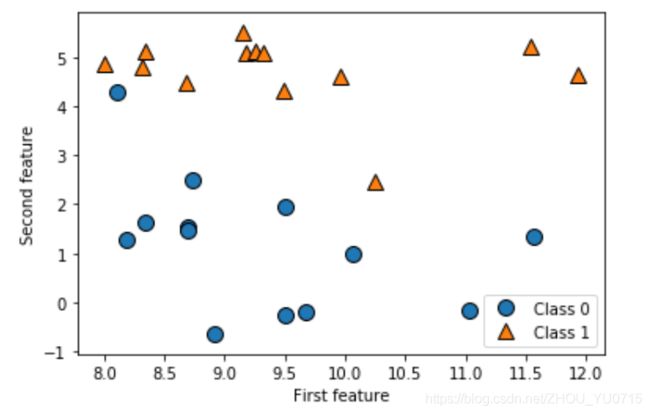
26个数据点和2个特征
回归算法数据集实例->wave数据集
X, y = mglearn.datasets.make_wave(n_samples=40)
plt.plot(X, y, 'o')
plt.ylim(-3, 3)
plt.xlabel("Feature")
plt.ylabel("Target")
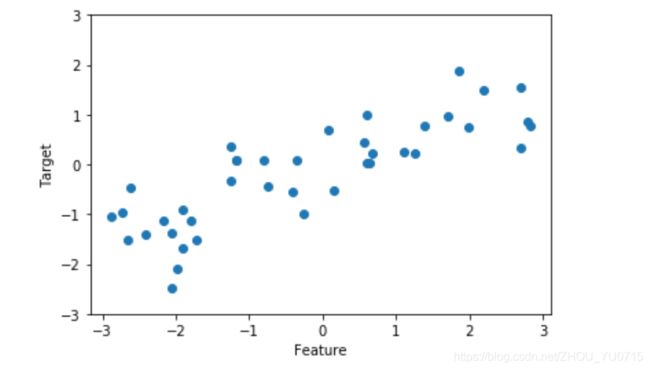
上述两个数据集为小型的数据集，针对现实生活中，存在很多现实问题的数据，通常比较庞大。
例如：scikit-learn中，有一个威斯康星洲乳腺癌数据集（cancer）。
可以使用scikit-learn模块的load_breast_cancer函数来进行加载。
还有一个最为常用的数据集为波士顿房价的数据集。
（2）k近邻
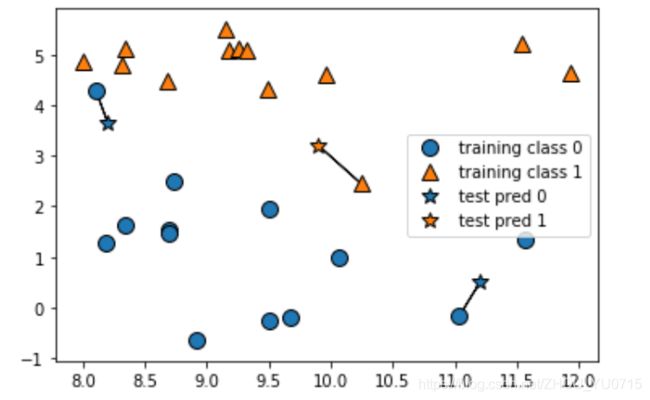
基于forge数据集上的应用：
mglearn.plots.plot_knn_classification(n_neighbors=1)
进行多个邻居判断的投票法：
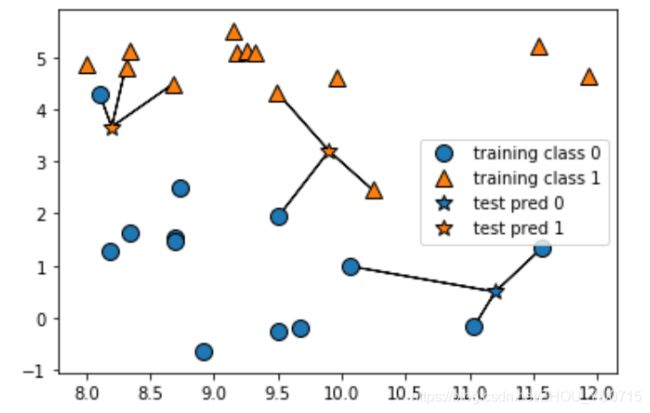
mglearn.plots.plot_knn_classification(n_neighbors=3)
from sklearn.model_selection import train_test_split #引入数据集分割模块
from sklearn.neighbors import KNeighborsClassifier #引入k邻近算法模块
X, y = mglearn.datasets.make_forge() #引入数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) #对数据集进行分割 每次输出相同的数据集
clf = KNeighborsClassifier(n_neighbors=3) #设置邻近算法k值
clf.fit(X_train, y_train) #保存数据集
print("Test set predictions: {}".format(clf.predict(X_test))) #计算训练集的最近邻，找出次数最多的类别
print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test))) #利用score方法进行评判模型的泛化能力好坏
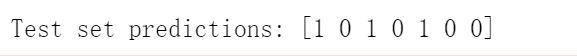
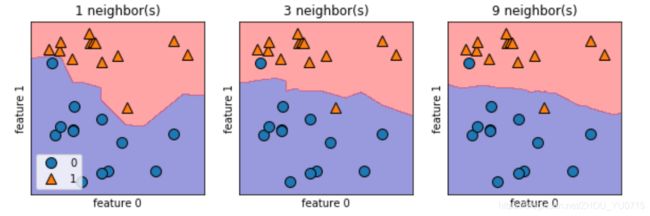
分析KNeighborsClassifier
对于二维数据集，我们还可以在 xy 平面上画出所有可能的测试点的预测结果。我们根据平面中每个点所属的类别对平面进行着色。这样可以查看决策边界（decision boundary），即算法对类别 0 和类别 1 的分界线。
fig, axes = plt.subplots(1, 3, figsize=(10, 3)) #绘制一个一行三列共3个子图；fig是主图，axes是子图
for n_neighbors, ax in zip([1, 3, 9], axes):
# fit方法返回对象本身，所以我们可以将实例化和拟合放在一行代码中
clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{} neighbor(s)".format(n_neighbors))
ax.set_xlabel("feature 0")
ax.set_ylabel("feature 1")
axes[0].legend(loc=3) #loc表示legend的位置是在左下角、右下角还是上边
模型复杂度和泛化能力
from sklearn.datasets import load_breast_cancer#引入cancer数据集模块
cancer = load_breast_cancer()#导入数据集
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=66)#数据分割
training_accuracy = []#训练集精度
test_accuracy = []#测试集精度
# n_neighbors取值从1到10
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
# 构建模型
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train, y_train)
# 记录训练集精度
training_accuracy.append(clf.score(X_train, y_train))
# 记录泛化精度
test_accuracy.append(clf.score(X_test, y_test))
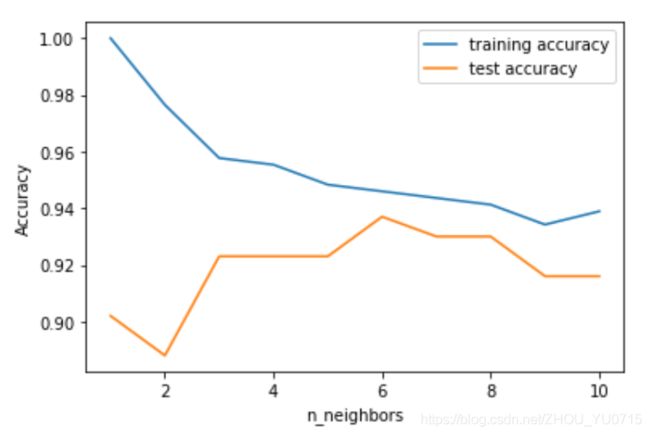
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()
当邻居数大约为6时，性能最佳。
k近邻回归
使用wave数据集
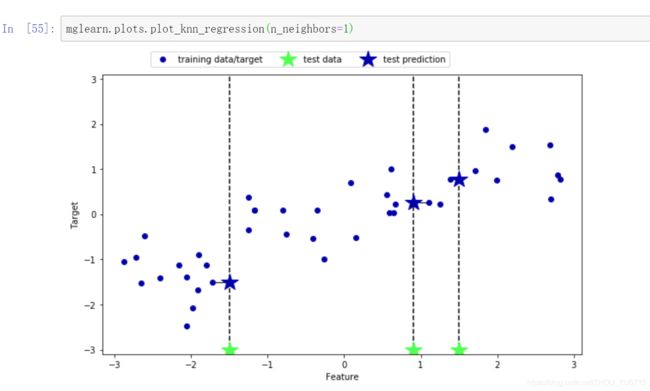
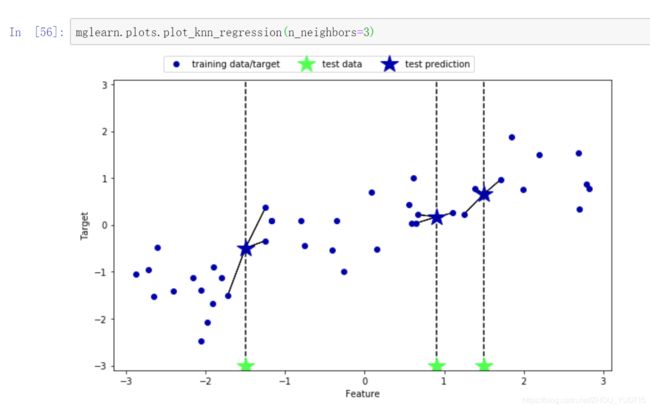
用于回归的 k 近邻算法在 scikit-learn 的 KNeighborsRegressor 类中实现。
from sklearn.neighbors import KNeighborsRegressor
X, y = mglearn.datasets.make_wave(n_samples=40)
# 将wave数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 模型实例化，并将邻居个数设为3
reg = KNeighborsRegressor(n_neighbors=3)
# 利用训练数据和训练目标值来拟合模型
reg.fit(X_train, y_train)
print("Test set predictions:\n{}".format(reg.predict(X_test)))
print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test)))
在回归问题中，使用score方法来进行评估模型时，返回R^2分数，这个分数也叫做决定系数，是回归模型预测的优良度度量。
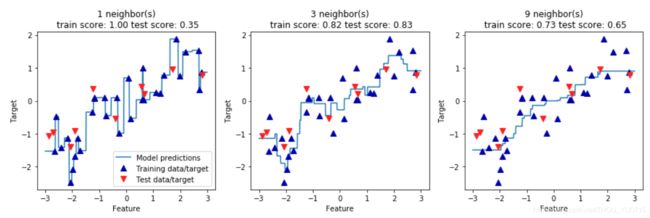
分析KNeighborRegressor
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 创建1000个数据点，在-3和3之间均匀分布
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
# 利用1个、3个或9个邻居分别进行预测
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
ax.set_title("{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(
n_neighbors, reg.score(X_train, y_train),reg.score(X_test, y_test)))
ax.set_xlabel("Feature")
ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target","Test data/target"], loc="best")
优点、缺点和参数
下面介绍的模型，就没有KNN的这些缺点。
（3）线性模型
线性模型是在实践中广泛使用的一类模型。线性模型利用输入特征的**线性函数（liinear function）**进行预测。
用于回归的线性模型
线性模型预测的一般公式如下：
ŷ = w[0] * x[0] + w[1] * x[1] + … + w[p] * x[p] + b
这里 x[0] 到 x[p] 表示单个数据点的特征（本例中特征个数为 p+1），w 和 b 是学习模型的参数，ŷ 是模型的预测结果。对于单一特征的数据集，公式如下：
ŷ = w[0] * x[0] + b
线性回归（普通最小二乘法）
线性回归，或者普通最小二乘法（ordinary least squares，OLS），是回归问题最简单也最经典的线性方法。线性回归寻找参数 w 和 b，使得对训练集的预测值与真实的回归目标值 y之间的均方误差最小。均方误差（mean squared error）是预测值与真实值之差的平方和除以样本数。线性回归没有参数，这是一个优点，但也因此无法控制模型的复杂度。
from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 42)
lr = LinearRegression().fit(X_train, y_train)
print("lr.coef_:{}".format(lr.coef_)) #斜率 w 权重或系数
print("lr.intercept_:{}".format(lr.intercept_)) #截距 b
print("Training set score:{:.2f}".format(lr.score(X_train,y_train)))
print("Test set score:{:.2f}".format(lr.score(X_test,y_test)))
你可能注意到了 coef_ （coefficient）和 intercept_ 结尾处奇怪的下划线。scikit-learn总是将从训练数据中得出的值保存在以下划线结尾的属性中。这是为了将其与用户设置的参数区分开。
训练集和测试集上的分数非常接近。这说明可能存在欠拟合，而不是过拟合。对于这个一维数据集来说，过拟合的风险很小，因为模型非常简单（或受限）。然而，对于更高维的数据集（即有大量特征的数据集），线性模型将变得更加强大，过拟合的可能性也会变大。
我们来看一下波士顿放假数据集更加复杂一些的情况的线性回归模型。
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
print("Training set score:{:.2f}".format(lr.score(X_train, y_train)))
print("Test set score:{:.2f}".format(lr.score(X_test, y_test)))
这也就是过拟合的标志。
标准线性回归最常用的替代方法之一是岭回归（ridge regression）。
岭回归
系数接近于0，通常默认alpha= 1.0，用户通过设置alpha参数来指定。
