机器学习（一） 使用KNN实现车辆图像分类

机器学习（二） 使用KNN实现车辆图像分类

---

---

前言

本文中的车辆数据集图像于集美大学拍摄。本文中记录了使用KNN算法对车辆图像进行分类的过程。

参考文章：

https://blog.csdn.net/vendetta_gg/article/details/106599718
https://blog.csdn.net/CltCj/article/details/117550045

---

一、车辆数据集

该数据集总共有31张图片，包括car、bicycle、electric bicycle共三个分类。car类别有10张，bicycle类别有11张，electric bicycle类别有10张。

1.车辆数据集示例

car:

bicycle:

electric bicycle:

bicycle文件夹:

二、KNN算法

1.KNN算法介绍

KNN(K-Nearest Neighbor)算法是数据挖掘分类技术中最简单的方法之一。该算法就是使用一个样本在特征空间当中最近的k个样本的最多的类别来表示该样本的类别。

2.KNN算法步骤

1、计算出测试样本与各个训练样本之间的距离；
2、递增排序；
3、找到距离最小的K个点；
4、找到这K个点中出现最多的类别作为测试样本的类别。

3.KNN算法优点

1、简单、易于理解与实现，无估计参数；
2、预测效果好；
3、适合对稀有事件进行分类；
4、适用于多分类问题。

4.KNN算法缺点

1、样本不平衡时，预测结果可能会受到样本数多的类别影响；
2、计算量较大，每一个预测样本都需要与全体训练样本计算距离。

5.K值选取

由于K值太小容易过拟合，K值过大又会欠拟合，需要选取合适的K值。

1、根据经验选取；2、从一个较小的K值开始增加，每次计算测试集的错误率，选取错误率最小的K。

6.距离度量

6.1 欧式距离

欧式距离指在m维空间中两个点之间的真实距离。

$$d(x,y)=\sqrt{\sum _{i=1}^n{(X_i-Y_i)}^2}$$

6.曼哈顿距离

欧式距离的局限是只能度量两点之间的直线距离。但现实世界中，往往直走不能到达目的地。

$$d(x,y)=\sum _{i=1}^n\left|X_i-Y_i\right|$$

三、代码实现

1.数据集

1.1数据集随机划分

data_split.py:

import os
import random
from shutil import copy2

def data_set_split(src_data_folder, target_data_folder, train_scale=0.8, val_scale=0.0, test_scale=0.2):
	#读取源数据文件夹，生成划分好的文件夹，分为trian、val、test三个文件夹
    if os.path.isdir(target_data_folder):
        pass
    else:
        os.mkdir(target_data_folder)
    print("开始数据集划分")
    class_names = os.listdir(src_data_folder)
    split_names = ['train', 'val', 'test']
    for split_name in split_names:
        split_path = os.path.join(target_data_folder, split_name)
        if os.path.isdir(split_path):
            pass
        else:
            os.mkdir(split_path)
        for class_name in class_names:
            class_split_path = os.path.join(split_path, class_name)
            if os.path.isdir(class_split_path):
                pass
            else:
                os.mkdir(class_split_path)

    for class_name in class_names:
        current_class_data_path = os.path.join(src_data_folder, class_name)
        current_all_data = os.listdir(current_class_data_path)
        current_data_length = len(current_all_data)
        current_data_index_list = list(range(current_data_length))
        random.shuffle(current_data_index_list)

        train_folder = os.path.join(os.path.join(target_data_folder, 'train'), class_name)
        val_folder = os.path.join(os.path.join(target_data_folder, 'val'), class_name)
        test_folder = os.path.join(os.path.join(target_data_folder, 'test'), class_name)
        train_stop_flag = current_data_length * train_scale
        val_stop_flag = current_data_length * (train_scale + val_scale)
        current_idx = 0
        train_num = 0
        val_num = 0
        test_num = 0
        for i in current_data_index_list:
            src_img_path = os.path.join(current_class_data_path, current_all_data[i])
            if current_idx <= train_stop_flag:
                copy2(src_img_path, train_folder)
                train_num = train_num + 1
            elif (current_idx > train_stop_flag) and (current_idx <= val_stop_flag):
                copy2(src_img_path, val_folder)
                val_num = val_num + 1
            else:
                copy2(src_img_path, test_folder)
                test_num = test_num + 1
            
            current_idx = current_idx + 1

        print("*********************************{}*************************************".format(class_name))
        print("{}类按照{}：{}：{}的比例划分完成，一共{}张图片".format(class_name, train_scale, val_scale, test_scale, current_data_length))
        print("训练集{}：{}张".format(train_folder, train_num))
        print("验证集{}：{}张".format(val_folder, val_num))
        print("测试集{}：{}张".format(test_folder, test_num))


if __name__ == '__main__':
    src_data_folder = "dataset"
    target_data_folder = "split_dataset"
    data_set_split(src_data_folder, target_data_folder)

参照 训练集:测试集=7:3 的划分结果：

最终得到训练集图片总数为24，测试集图片总数为7。

1.2数据集读取

由于希望一次性读出所有数据，这里的dataloader使用的batch_size就为训练集或测试集的大小。

# 加载数据集
import torch
import torchvision
import torchvision.transforms as transforms
import numpy as np
import operator

train_data_path = 'split_dataset/train'
test_data_path = 'split_dataset/test'

data_transforms ={
    'train': transforms.Compose([
        transforms.Resize(512),
        transforms.ToTensor(),
        transforms.Normalize([.5, .5, .5],[.5, .5, .5])
    ]),
    'test': transforms.Compose([
        transforms.Resize(512),
        transforms.ToTensor(),
        transforms.Normalize([.5, .5, .5],[.5, .5, .5])
    ])
}

train_dataset = torchvision.datasets.ImageFolder(train_data_path, transform=data_transforms['train'])
test_dataset = torchvision.datasets.ImageFolder(test_data_path, transform=data_transforms['test'])

train_loader=torch.utils.data.DataLoader(dataset=train_dataset,
                                         batch_size=24,
                                         shuffle=True)
test_loader=torch.utils.data.DataLoader(dataset=test_dataset,
                                        batch_size=7,
                                        shuffle=False)
for data in train_loader:
    X_train, Y_train = data
    X_train = X_train.flatten(1)

for data in test_loader:
    X_test, Y_test = data
    X_test = X_test.flatten(1)

X_train, Y_train = X_train.numpy(), Y_train.numpy()
X_test, Y_test = X_test.numpy(), Y_test.numpy()

2.KNN分类器

# KNN分类器
def KNN(k, d_type, X_train, Y_train, X_test):
    '''
    :param k: k个最近点
    :param d_type: 曼哈顿距离 or 欧几里得距离
    :param X_train: 训练样本图片
    :param X_test: 训练样本标签
    :param Y_train: 测试样本图片
    '''
    
    #判断是否属于曼哈顿距离或欧几里得距离
    assert d_type == 'M' or d_type == 'E' 
    
    Y_test = []
    num_test = X_test.shape[0]
    
    for i in range(num_test):
        if d_type == 'M':
            distance = np.sum(np.abs(X_train - np.tile(X_test[i], (X_train.shape[0],1))), 1)
        if d_type == 'E':
            distance = np.sqrt(np.sum((X_train - np.tile(X_test[i], (X_train.shape[0], 1))**2), 1))
        sorted_index = np.argsort(distance)
        top_k = sorted_index[:k]
        cnt = {}
        for j in top_k:
            cnt[Y_train[j]] = cnt.get(Y_train[j], 0) + 1
        sorted_cnt = sorted(cnt.items(), key=operator.itemgetter(1), reverse=True)
        Y_test.append(sorted_cnt[0][0])
    return np.array(Y_test)

3.训练

3.1使用曼哈顿距离进行训练

acc_list = []
best_acc = 0
best_k = 0
for k in range(1,25):
    Y_test_pred = KNN(k, 'M', X_train, Y_train, X_test)
    num_correct = np.sum(Y_test_pred == Y_test)
    accuracy = float(num_correct) / X_test.shape[0]
    acc_list.append(accuracy)
    if accuracy > best_acc:
        best_acc = accuracy 
        best_k = k

print('best accuracy:', best_acc)

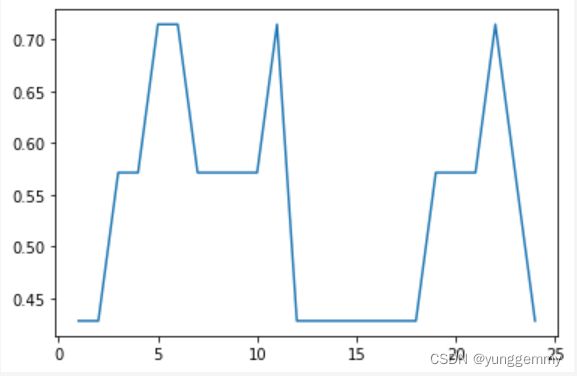
from matplotlib import pyplot as plt    
plt.plot(np.arange(1,25),acc_list)

结果：

3.2使用欧式距离进行训练

acc_list = []
best_acc = 0
best_k = 0
for k in range(1,25):
    Y_test_pred = KNN(k, 'E', X_train, Y_train, X_test)
    num_correct = np.sum(Y_test_pred == Y_test)
    accuracy = float(num_correct) / X_test.shape[0]
    acc_list.append(accuracy)
    if accuracy > best_acc:
        best_acc = accuracy 
        best_k = k

print('best accuracy:', best_acc)

from matplotlib import pyplot as plt    
plt.plot(np.arange(1,25),acc_list)

结果：

---

总结

使用欧式距离进行训练时，最佳的k值为24，accuracy为0.857，
使用曼哈顿距离进行训练时，最佳的k值为24，accuracy为0.715。

由于训练集总共只有24张，在选取k值时就从1一直遍历到24。但可以从accuracy的记录图中发现，无论是使用曼哈顿距离还是欧式距离作为距离的衡量方法，accuracy的变化都非常不稳定。这很有可能是因为该数据集每个类别都只有10张或11张图像，样本数量过少。