深度学习笔记1——正则化
必要说明:原版为Yoshua Bengio等编写的《Deep Learning》。根据开源中文版学习整理,仅作为学习使用。侵权请联系删除。
深度学习笔记——正则化
- 前言
- 一、参数范数惩罚
-
- 1.1 L²参数正则化
- 1.2 L¹参数正则化
- 二、数据集增强
- 三、半监督学习
- 四、多任务学习
- 五、提前终止(early stopping)
- 六、参数绑定和参数共享(parameter sharing)
- 七.稀疏表示
- 八、Bagging和其他集成方法
- 九、Dropout
- 十、对抗训练(adversarial training)
- 十一、切面距离、正切传播和流形正切分类器
前言
机器学习中的一个核心问题是设计不仅在训练数据上表现好,并且能在新输入上泛化好的算法。在机器学习中,许多策略显式地被设计为减少测试误差(可能会以增大训练误差为代价)。这些策略被统称为正则化。我们将正则化定义为 ‘‘对学习算法的修改——旨在减少泛化误差而不是训练误差”。
控制模型的复杂度不是找到合适规模的模型(带有正确的参数个数)这样一个简单的事情。相反,在实际的深度学习场景中我们几乎总是会发现,最好的拟合模型(从最小化泛化误差的意义上)是一个适当正则化的大型模型。
开发更有效的正则化策略已成为本领域的主要研究工作之一。
一、参数范数惩罚
许多正则化方法通过对目标函数 J 添加一个参数范数惩罚 Ω(θ),限制模型(如神经网络、线性回归或逻辑回归)的学习能力。我们将正则化后的目标函数(损失函数)记为J˜:
J ˜ ( θ ; X , y ) = J ( θ ; X , y ) + α Ω ( θ ) J˜(θ; X, y) = J(θ; X, y) + αΩ(θ) J˜(θ;X,y)=J(θ;X,y)+αΩ(θ)
其中,α ∈ [0, ∞) 是权衡范数惩罚项 Ω 和标准目标函数 J(X; θ) 相对贡献的超参数。将 α 设为 0 表示没有正则化。α 越大,对应正则化惩罚越大。
当我们的训练算法最小化正则化后的目标函数 J˜ 时,它会降低原始目标 J 关于训练数据的误差并同时减小参数 θ 的规模(或在某些衡量下参数子集的规模)。
说明:
在神经网络中我们通常只对每一层仿射变换的权重做惩罚而不对偏置做正则惩罚。精确拟合偏置所需的数据通常比拟合权重少得多。(每个偏置仅控制一个单变量。故我们不对其进行正则化也不会导致太大的方差。另外,正则化偏置参数可能会导致明显的欠拟合)。因此,我们使用向量 w 表示所有应受范数惩罚影响的权重,而向量 θ 表示所有参数 (包括 w 和无需正则化的参数。
1.1 L²参数正则化
通常被称为 权重衰减(weight decay),其策略是:通过向目标函数添加一个正则项 Ω ( θ ) = 1 2 ∥ w ∥ 2 2 Ω(θ) =\begin{array}{c}\frac{1}{2} \left \| w \right \| _{2}^{2} \end{array} Ω(θ)=21∥w∥22,使权重更加接近原点。在其他学术圈,L2 也被称为岭回归或 Tikhonov 正则。
通过研究正则化化后目标函数的梯度,洞察一些权重衰减的正则化表现。假定其中没有偏置参数,即 θ 就是 w。此模型具有以下总的目标函数:
J ~ ( w ; X , y ) = α 2 w ⊤ w + J ( w ; X , y ) , \begin{array}{c}\widetilde{J} \left ( w;X,y \right ) =\frac{\alpha }{2}w\ ^{\top } w+J\left ( w;X,y \right ) \end{array}, J (w;X,y)=2αw ⊤w+J(w;X,y),
其梯度为:
▽ w J ~ ( w ; X , y ) = α w + ▽ w J ( w ; X , y ) . \begin{array}{c} \bigtriangledown _{w} \widetilde{J} \left ( w;X,y \right ) =\alpha w+\bigtriangledown _{w} J\left ( w;X,y \right ) \end{array}. ▽wJ (w;X,y)=αw+▽wJ(w;X,y).
使用单步梯度下降更新权重,即执行以下更新:
w ← w − ϵ ( α w + ▽ w J ( w ; X , y ) ) . \begin{array}{c} w\gets w-\epsilon \left ( \alpha w+\bigtriangledown _{w} J\left ( w;X,y \right ) \right ) \end{array}. w←w−ϵ(αw+▽wJ(w;X,y)).
换一种写法:
w ← ( 1 − ϵ α ) w − ϵ ▽ w J ( w ; X , y ) . \begin{array}{c} w\gets \left ( 1-\epsilon \alpha \right ) w-\epsilon \bigtriangledown _{w} J\left ( w;X,y \right ) \end{array}. w←(1−ϵα)w−ϵ▽wJ(w;X,y).
发现加入权重衰减后会引起学习规则的修改,即在每步执行通常的梯度更
新之前先收缩权重向量(将权重向量乘以一个常数因子)。
说明:整个训练过程的分析已省略。总之,L2正则化能让学习算法 ‘‘感知’’ 到具有较高方差的输入 x,因此与输出目标的协方差较小(相对增加方差)的特征的权重将会收缩。
1.2 L¹参数正则化
除L²权重衰减,还可以使用L¹正则化来限制模型参数的规模。(可参考下面的七、稀疏表示)
对模型参数 w 的 L¹正则化被定义为: Ω ( θ ) = ∥ w ∥ 1 = ∑ i ∣ w i ∣ , \begin{array}{c} \Omega \left ( \theta \right ) =\left \| w \right \| _{1} =\sum_{i}^{} \left | w_{i} \right | \end{array}, Ω(θ)=∥w∥1=∑i∣wi∣,
即各个参数的绝对值之和。
与分析 L²正则化时一样不考虑偏置参数,通过缩放惩罚项 Ω 的正超参数 α来控制 L1权重衰减的强度。正则化的目标函数 J ~ ( w ; X , y ) \begin{array}{c}\widetilde{J} \left ( w;X,y \right ) \end{array} J (w;X,y)表示为:
J ~ ( w ; X , y ) = α ∥ w ∥ 1 + J ( w ; X , y ) , \begin{array}{c}\widetilde{J} \left ( w;X,y \right ) =\alpha \left \| w \right \| _{1} +J\left ( w;X,y \right ) \end{array}, J (w;X,y)=α∥w∥1+J(w;X,y),
其梯度为:
▽ w J ~ ( w ; X , y ) = α s i g n ( w ) + ▽ w J ( w ; X , y ) , \begin{array}{c} \bigtriangledown _{w} \widetilde{J} \left ( w;X,y \right ) =\alpha sign\left ( w \right ) +\bigtriangledown _{w} J\left ( w;X,y \right ) \end{array}, ▽wJ (w;X,y)=αsign(w)+▽wJ(w;X,y),
其中,sign(w)指取w各个元素的正负号。可以看到正则化对梯度的影响不再是线性地缩放每个 wi,而是添加了一项与sign(wi) 同号的常数。
说明:具体分析已省略。相比 L2正则化,L1正则化会产生更 稀疏(sparse)的解(参数)。此处稀疏性指的是最优值中的一些参数为 0(或接近于0)。和 L2正则化相比,L1正则化的稀疏性具有本质的不同。
二、数据集增强
让机器学习模型泛化得更好的最好办法是使用更多的数据进行训练。而在实践中,我们拥有的数据量是很有限的。解决这个问题的一种方法是创建假数据并添加到训练集中。对于一些机器学习任务(如分类),创建新的假数据相当简单。
在神经网络的输入层注入噪声也可以被看做是数据增强的一种方式。然而,神经网络被证明对噪声不是非常健壮 (Tang and Eliasmith, 2010)。改善神经网络健壮性的方法之一是简单地将随机噪声添加到输入再进行训练。向隐藏单元施加噪声也是可行的,这可以被看作在多个抽象层上进行的数据集增强。
通常情况下,人工设计的数据集增强方案可以大大减少机器学习技术的泛化误差。
说明:噪声鲁棒性
1.在一般情况下,噪声注入远比简单地收缩参数强大,特别是噪声被添加到隐藏单元时会更加强大。下面所述的 Dropout 算法是这种做法的主要发展方向。
2.另一种正则化模型的噪声使用方式是将其加到权重。这项技术主要用于循环神经网络 (Jim et al., 1996; Graves, 2011)。
3.向输出目标注入噪声。对于一些小常数 ϵ,训练集标记 y 是正确的概率是 1 − ϵ,(以 ϵ 的概率)任何其他可能的标签也可能是正确的。标签平滑(Label smoothing) :通过把确切分类目标从 0 和 1 替换成 ϵ k − 1 \begin{array}{c}\frac{\epsilon }{k-1} \end{array} k−1ϵ 和 1 − ϵ,正则化具有 k 个输出的 softmax 函数的模型,标签平滑的优势是能够防止模型追求确切概率而不影响模型学习正确分类。
三、半监督学习
四、多任务学习
多任务学习 (Caruana, 1993) 是通过合并几个任务中的样例(可以视为对参数施加的软约束)来提高泛化的一种方式。额外的训练样本以同样的方式将模型的参数推向泛化更好的方向,当模型的一部分在任务之间共享时,模型的这一部分更多地被约束为良好的值(假设共享是合理的),往往能更好地泛化。
说明:该模型参数通常可分为两种:
1.具体任务的参数(只能从各自任务的样本中实现良好泛化),如h(1),h(2),h(3);
2.所有任务共享的通用参数(从所有任务的汇集数据中获益),如h(shared)。
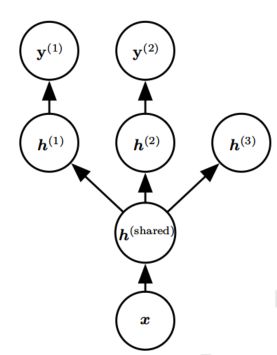
因为共享参数,其统计强度可大大提高(共享参数的样本数量相对于单任务模式增加的比例),并能改善泛化和泛化误差的范围 (Baxter, 1995)。
五、提前终止(early stopping)
当训练有足够的表示能力甚至会过拟合的大模型时,我们经常观察到,训练误差会随着时间的推移逐渐降低,但验证集的误差会再次上升。这种现象几乎一定会出现。
如果我们返回使验证集误差最低的参数设置,就可以获得更好的模型(因此,有希望获得更好的测试误差)。在每次验证集误差有所改善后,我们存储模型参数的副本。当训练算法终止时,我们返回这些参数而不是最新的参数。当验证集上的误差在事先指定的循环次数内没有进一步改善时,算法就会终止。它的流行主要是因为有效性和简单性。
通过提前终止自动选择超参数的唯一显著的代价是训练期间要定期评估验证集。另一个提前终止的额外代价是需要保持最佳的参数副本,这种代价一般是可忽略的。
提前终止可单独使用或与其他的正则化策略结合使用。
提前终止对减少训练过程的计算成本也是有用的。除了由于限制训练的迭代次
数而明显减少的计算成本,还带来了正则化的益处(不需要添加惩罚项的代价函
数或计算这种附加项的梯度)。
提前终止有两种基本策略,用于第二轮训练过程:
1.再次初始化模型,然后使用所有数据再次训练。在这个第二轮训练过程中,我们使用第一轮提前终止训练确定的最佳步数。
说明:由于训练集变大了,在第二轮训练时,每一次遍历数据集将会更多次地更新参数。
2.保持从第一轮训练获得的参数,然后使用全部的数据继续训练。在这个阶段,已经没有验证集指导我们需要在训练多少步后终止。我们可以监控验证集的平均损失函数,并继续训练,直到它低于提前终止过程终止时的目标值。
说明:此策略避免了重新训练模型的高成本,但表现并没有那么好。例如,验证集的目标不一定能达到之前的目标值,所以这种策略甚至不能保证终止。
六、参数绑定和参数共享(parameter sharing)
这种方法由Lasserre et al. (2006) 提出,正则化一个模型(监督模式下训练的分类器)的参数,使其接近另一个无监督模式下训练的模型(捕捉观察到的输入数据的分布)的参数。
和正则化参数使其接近(通过范数惩罚)相比,参数共享的一个显著优点是,只有参数(唯一一个集合)的子集需要被存储在内存中。对于某些特定模型,如卷积神经网络,这可能可以显著减少模型所占用的内存。
说明:如最流行和最广泛应用于CV的卷积神经网络(CNN)。
七.稀疏表示
前文所述的权重衰减直接惩罚模型参数。另一种是惩罚神经网络中的激活单元,稀疏化激活单元。
含有隐藏单元的模型在本质上都能变得稀疏。
八、Bagging和其他集成方法
Bagging(bootstrap aggregating)是通过结合几个模型降低泛化误差的技术(Breiman, 1994)。主要想法是分别训练几个不同的模型,然后让所有模型表决测试样例的输出。这是机器学习中常规策略的一个例子,被称为 模型平均(model averaging)。采用这种策略的技术被称为集成方法。
九、Dropout
Dropout提供了一种廉价的Bagging集成近似,能够训练和评估指数级数量的神经网络。
最先进的神经网络基于一系列仿射变换和非线性变换,我们只需将一些单元的输出乘零就能有效地删除一个单元。
Dropout训练与Bagging训练不太一样:
在Bagging的情况下,所有模型都是独立的;在Dropout的情况下,所有模型共享参数,其中每个模型继承父神经网络参数的不同子集。参数共享使得在有限可用的内存下表示指数级数量的模型变得可能。
在Bagging的情况下,每一个模型在其相应训练集上训练到收敛。在Dropout的情况下,通常大部分模型都没有显式地被训练,而是在单个步骤中我们训练一小部分的子网络,参数共享会使得剩余的子网络也能有好的参数设定。
Srivastava et al. (2014) 显示,Dropout比其他标准的计算开销小的正则化方法(如权重衰减、过滤器范数约束和稀疏激活的正则化)更有效。Dropout也可以与其他形式的正则化合并,得到进一步的提升。
另一个显著优点是不怎么限制适用的模型或训练过程。几乎在所有使用分布式表示且可以用随机梯度下降训练的模型上都表现很好。
说明:
1.只有极少的训练样本可用时,Dropout不会很有效。
2.随机性对实现Dropout的正则化效果不是必要的,同时也不是充分的。
3.另一种深度学习算法——批标准化(Batch Normalization),在训练时向隐藏单元引入加性和乘性噪声重新参数化模型。批标准化的主要目的是改善优化,但噪声具有正则化的效果,有时没必要再使用Dropout。
十、对抗训练(adversarial training)
十一、切面距离、正切传播和流形正切分类器
略