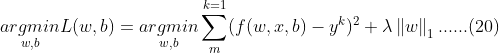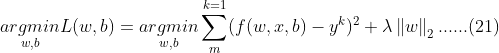《Python机器学习及实践:从零开始通往Kaggle竞赛之路》第3章 进阶篇 学习笔记(四)3.1.2.2L1范数正则化、3.1.2.3L2范数正则化总结
目录
3.1.2.2L1范数正则化
1、L1范数正则化
2、编程实践
3、总结
3.1.2.3L2范数正则化
1、L2范数正则化
2、编程实践
3、总结
3.1.2.2L1范数正则化
1、L1范数正则化
正则化的目的在于提高模型在未知测试数据上的泛化力,避免参数过拟合。由上一节的“比萨饼价格预测”的例子可以看出,2次多项式回归是相对较好的模型假设。之所以出现如4次多项式那样的过拟合情景,是由于4次方项对于的系数过大,或者不为0所导致。
因此,正则化的常见方法都是在原模型优化目标的基础上,增加对参数的惩罚(Penalty)项。以在“2.1.2.1线性回归器总结”一节中介绍过的最小二乘优化目标为例,如果加入对模型的![]() 范数正则化,那么新的线性回归目标如式(20)所示。
范数正则化,那么新的线性回归目标如式(20)所示。
也就是说,在原优化目标的基础上,增加了参数向量的![]() 范数。如此一来,在新目标优化的过程中,也同时需要考量
范数。如此一来,在新目标优化的过程中,也同时需要考量![]() 惩罚项的影响。为了使目标最小化,这种正则化方法的结果会让参数向量中许多元素趋向于0,使得大部分特征失去对优化目标的贡献。而这种让有效特征变得稀疏的
惩罚项的影响。为了使目标最小化,这种正则化方法的结果会让参数向量中许多元素趋向于0,使得大部分特征失去对优化目标的贡献。而这种让有效特征变得稀疏的![]() 正则化模型,通常被称为Lasso。
正则化模型,通常被称为Lasso。
2、编程实践
接下来,在上一节例子的基础上,继续使用4次多项式特征,但是换成Lasso模型检验![]() 范数正则化后的性能和参数。
范数正则化后的性能和参数。
# 代码60:使用线性回归模型在比萨训练样本上进行拟合
# 输入训练样本的特征以及目标值,分别存储在变量X_train与y_train之中。
X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
# 从sklearn.linear_model中导入LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归模型。
regressor = LinearRegression()
# 直接以披萨的直径作为特征训练模型。
regressor.fit(X_train, y_train)
# 导入numpy并且重命名为np。
import numpy as np
# 在x轴上从0至25均匀采样100个数据点。
xx = np.linspace(0, 26, 100)
xx = xx.reshape(xx.shape[0], 1)
# 以上述100个数据点作为基准,预测回归直线。
yy = regressor.predict(xx)
# 对回归预测到的直线进行作图。
import matplotlib.pyplot as plt
plt.scatter(X_train, y_train)
plt1, = plt.plot(xx, yy, label="Degree=1")
plt.axis([0, 25, 0, 25])
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.legend(handles=[plt1])
plt.show()
# 输出线性回归模型在训练样本上的R-squared值。
print('The R-squared value of Linear Regressor performing on the training data is', regressor.score(X_train, y_train))
# 代码61:使用2次多项式回归模型在比萨训练样本上进行拟合
# 从sklearn.preproessing中导入多项式特征产生器。
from sklearn.preprocessing import PolynomialFeatures
# 使用PolynominalFeatures(degree=2)映射出2次多项式特征,存储在变量X_train_poly2中。
poly2 = PolynomialFeatures(degree=2)
X_train_poly2 = poly2.fit_transform(X_train)
# 以线性回归器为基础,初始化回归模型。尽管特征的维度有提升,但是模型基础仍然是线性模型。
regressor_poly2 = LinearRegression()
# 对2次多项式回归模型进行训练。
regressor_poly2.fit(X_train_poly2, y_train)
# 从新映射绘图用x轴采样数据。
xx_poly2 = poly2.transform(xx)
# 使用2次多项式回归模型对应x轴采样数据进行回归预测。
yy_poly2 = regressor_poly2.predict(xx_poly2)
# 分别对训练数据点、线性回归直线、2次多项式回归曲线进行作图。
plt.scatter(X_train, y_train)
plt1, = plt.plot(xx, yy, label='Degree=1')
plt2, = plt.plot(xx, yy_poly2, label='Degree=2')
plt.axis([0, 25, 0, 25])
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.legend(handles=[plt1, plt2])
plt.show()
# 输出2次多项式回归模型在训练样本上的R-squared值。
print('The R-squared value of Polynominal Regressor (Degree=2) performing on the training data is', regressor_poly2.score(X_train_poly2, y_train))
# 代码62:使用4次多项式回归模型在比萨训练样本上进行拟合
# 从sklearn.preprocessing导入多项式特征生成器。
from sklearn.preprocessing import PolynomialFeatures
# 初始化4次多项式特征生成器。
poly4 = PolynomialFeatures(degree=4)
X_train_poly4 = poly4.fit_transform(X_train)
# 使用默认配置初始化4次多项式回归器。
regressor_poly4 = LinearRegression()
# 对4次多项式回归模型进行训练。
regressor_poly4.fit(X_train_poly4, y_train)
# 从新映射绘图用x轴采样数据。
xx_poly4 = poly4.transform(xx)
# 使用4次多项式回归模型对应x轴采样数据进行回归预测。
yy_poly4 = regressor_poly4.predict(xx_poly4)
# 分别对训练数据点、线性回归直线、2次多项式以及4次多项式回归曲线进行作图。
plt.scatter(X_train, y_train)
plt1, = plt.plot(xx, yy, label='Degree=1')
plt2, = plt.plot(xx, yy_poly2, label='Degree=2')
plt4, = plt.plot(xx, yy_poly4, label='Degree=4')
plt.axis([0, 25, 0, 25])
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.legend(handles=[plt1, plt2, plt4])
plt.show()
print('The R-squared value of Polynominal Regressor (Degree=4) performing on the training data is', regressor_poly4.score(X_train_poly4, y_train))
# 代码63:评估3种回归模型在测试数据集上的性能表现
# 准备测试数据。
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
# 使用测试数据对线性回归模型的性能进行评估。
regressor.score(X_test, y_test)
print(regressor.score(X_test, y_test))
# 使用测试数据对2次多项式回归模型的性能进行评估。
X_test_poly2 = poly2.transform(X_test)
regressor_poly2.score(X_test_poly2, y_test)
print(regressor_poly2.score(X_test_poly2, y_test))
# 使用测试数据对4次多项式回归模型的性能进行评估。
X_test_poly4 = poly4.transform(X_test)
regressor_poly4.score(X_test_poly4, y_test)
print(regressor_poly4.score(X_test_poly4, y_test))
# 代码64:Lasso模型在4次多项式特征上的拟合表现
# 从sklearn.linear_model中导入Lasso。
from sklearn.linear_model import Lasso
# 使用默认配置初始化Lasso。
lasso_poly4 = Lasso()
# 使用Lasso对4次多项式特征进行拟合。
lasso_poly4.fit(X_train_poly4, y_train)
# 对Lasso模型在测试样本上的回归性能进行评估。
print(lasso_poly4.score(X_test_poly4, y_test))
# 输出Lasso模型的参数列表。
print(lasso_poly4.coef_)
# 回顾普通4次多项式回归模型过拟合之后的性能。
print(regressor_poly4.score(X_test_poly4, y_test))
# 回顾普通4次多项式回归模型的参数列表。
print(regressor_poly4.coef_)本地输出:
0.8388926873604382
[ 0.00000000e+00 0.00000000e+00 1.17900534e-01 5.42646770e-05
-2.23027128e-04]
0.8095880795766807
[[ 0.00000000e+00 -2.51739583e+01 3.68906250e+00 -2.12760417e-01
4.29687500e-03]]3、总结
通过对一系列输出的观察,验证了所介绍的Lasso模型的一切特点:
①相比于普通4次多项式回归模型在测试集上的表现,默认配置的Lasso模型性能提高了大约3%。
②相较之下,Lasso模型拟合后的参数列表中,4次与3次特征的参数均为0.0,使得特征更加稀疏。
3.1.2.3L2范数正则化
1、L2范数正则化
与![]() 范数正则化略有不同的是,
范数正则化略有不同的是,![]() 范数正则化则在原优化目标的基础上,增加了参数向量的
范数正则化则在原优化目标的基础上,增加了参数向量的![]() 范数的惩罚项,如公式(21)所示。为了使新优化目标最小化,这种正则化方法的结果会让参数向量中的大部分元素都变得很小,压制了参数之间的差异性。而这种压制参数之间差异性的
范数的惩罚项,如公式(21)所示。为了使新优化目标最小化,这种正则化方法的结果会让参数向量中的大部分元素都变得很小,压制了参数之间的差异性。而这种压制参数之间差异性的![]() 正则化模型,通常被称为Ridge。
正则化模型,通常被称为Ridge。
2、编程实践
接下来,在上一节例子的基础上,继续对4次多项式特征,但是换成Ridge模型检验![]() 范数正则化后的性能和参数。
范数正则化后的性能和参数。
# 代码65:Ridge模型在4次多项式特征上的拟合表现
# 输出普通4次多项式回归模型的参数列表。
print(regressor_poly4.coef_)
# 输出上述这些参数的平方和,验证参数之间的巨大差异。
print(np.sum(regressor_poly4.coef_ ** 2))
# 从sklearn.linear_model导入Ridge。
from sklearn.linear_model import Ridge
# 使用默认配置初始化Ridge。
ridge_poly4 = Ridge()
# 使用Ridge模型对4次多项式特征进行拟合。
ridge_poly4.fit(X_train_poly4, y_train)
# 输出Ridge模型在测试样本上的回归性能。
print(ridge_poly4.score(X_test_poly4, y_test))
# 输出Ridge模型的参数列表,观察参数差异。
print(ridge_poly4.coef_)
# 计算Ridge模型拟合后参数的平方和。
print(np.sum(ridge_poly4.coef_ ** 2))本地输出:
[[ 0.00000000e+00 -2.51739583e+01 3.68906250e+00 -2.12760417e-01
4.29687500e-03]]
647.3826457369564
0.8374201759366577
[[ 0. -0.00492536 0.12439632 -0.00046471 -0.00021205]]
0.0154989652035710163、总结
通过对一系列输出的观察,可以验证Ridge模型的一切特点:
①相比于普通4次多项式回归模型在测试集上的表现,默认配置的Ridge模型性能提高了近3%。
②与普通4次多项式回归模型不同的是,Ridge模型拟合后的参数之间差异非常小。
备注:不论是公式(20)还是公式(21)中的惩罚项,都会有一个因子![]() 进行调节。尽管
进行调节。尽管![]() 不属于需要拟合的参数,却在模型优化中扮演非常重要的角色。
不属于需要拟合的参数,却在模型优化中扮演非常重要的角色。