强化学习--马尔可夫决策过程学习笔记
本文学习内容参照视频
1、强化学习
基本概念:强化学习是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论,即有机体如何在环境给予的奖励或惩罚的刺激下,逐步形成对刺激的预期,产生能获得最大利益的习惯性行为。
2、马尔可夫决策过程
强化学习的常见模型是标准的马尔可夫决策过程(Markov Decision Process, MDP)
2.1 马尔可夫过程
马尔可夫过程 = 状态 + 状态转移概率
马尔可夫性质:未来只与当前状态有关,与过去无关。其数学定义为:
P [ S t + 1 ∣ S t ] = P [ S t + 1 ∣ S 1 , … , S t ] P\left[S_{t+1} \mid S_{t}\right]=P\left[S_{t+1} \mid S_{1}, \ldots, S_{t}\right] P[St+1∣St]=P[St+1∣S1,…,St]
即在状态 S t S_{t} St的条件下转移 S t + 1 S_{t+1} St+1状态的概率等于在状态 S 1 , … , S t S_{1}, \ldots, S_{t} S1,…,St都发生的条件下转移到状态 S t + 1 S_{t+1} St+1的概率。其中 [ S 1 , … , S t ] [S_{1}, \ldots, S_{t}] [S1,…,St]为有限随机状态序列。

转移概率
就是从一种状态转移到另一种状态的概率。通常使用状态转移矩阵来表示。
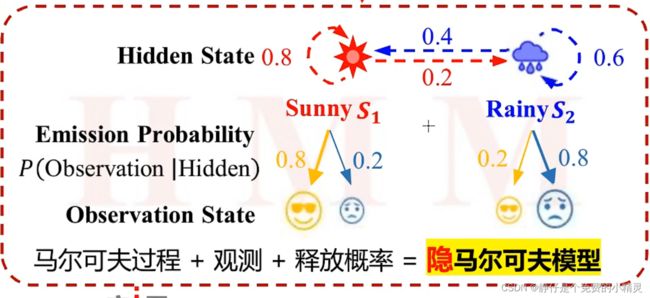
2.2 隐马尔可夫模型
隐马尔科夫模型 = 马尔科夫过程+观测+释放概率
已知其中两个,就可以对另一个进行预测
马尔可夫奖励过程
2.2 马尔可夫奖励过程
马尔可夫奖励过程 = 马尔可夫过程+ 奖励
即时奖励:
长期奖励 G t G_t Gt:
与状态转移链相伴生,不同状态转移链对应不同的长期奖励
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = ∑ k = 0 ∞ γ k R t + k + 1 G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\dots= \sum\limits_{k=0}^{\infty}\gamma^k R_{t+k+1} Gt=Rt+1+γRt+2+γ2Rt+3+⋯=k=0∑∞γkRt+k+1
其中 γ \gamma γ为衰减系数,表示即时奖励在当前的折扣值, γ ∈ ( 0 , 1 ) \gamma \in(0,1) γ∈(0,1)
R t + 1 R_{t+1} Rt+1表示转移到状态 S t + 1 S_{t+1} St+1的奖励
价值函数 V ( S ) V(S) V(S)
不管是即时奖励还是长期奖励,都是对状态转移过程的评价,使用价值函数对状态进行评价
V ( S t ) = E [ G t ∣ s = S t ] V(S_t)=E[G_t|s=S_t] V(St)=E[Gt∣s=St]
由转态 S t S_t St为起点可以有多条转态转移链,每一条链都有一个长期折扣奖励 G t G_t Gt,使用以 s t s_t st为起点的所有状态转移链 G t G_t Gt的期望作为衡量 S t S_t St价值的指标
2.3 马尔可夫决策过程
马尔可夫决策过程 = 马尔可夫奖励过程 + 动作(动作产生不确定的状态转移)
如果动作产生确定的状态转移,就是动态规划 (最短路径问题,其中路段成本为状态转移的奖励)
定义马尔可夫决策过程是一个元组 < S , A , P , R , γ >
S S S表示状态的集合
A A A表示动作的集合
P P P表示状态转移概率矩阵
R R R表示奖励函数
γ \gamma γ表示折扣因子 γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]
