2020-4-5 深度学习笔记17 - 蒙特卡罗方法 3 ( 马尔可夫链蒙特卡罗方法MCMC-先验分布/后验分布/似然估计，马尔可夫性质)

第十七章 蒙特卡罗方法

中文
英文

2020-4-4 深度学习笔记17 - 蒙特卡罗方法 1 (采样和蒙特卡罗方法-必要性和合理性)
2020-4-4 深度学习笔记17 - 蒙特卡罗方法 2 ( 重要采样–采样数量一定，提高准确度，减少方差)

马尔可夫链蒙特卡罗方法MCMC

关于马尔可夫链蒙特卡洛方法（Markov chain Monte Carlo/MCMC）

• 解释1：是一种使用了“马尔可夫链”的“蒙特卡罗”（即随机）方法。显然，MCMC是一种蒙特卡罗方法。
• 解释2：通过在概率空间中随机采样以近似兴趣参数（parameter of interest）的后验分布。或者说从某些模型的后验概率分布中抽取样本
• 解释3：为了在一个指定的分布上采样，根据马尔可夫过程，首先从任一状态出发，模拟马尔可夫过程，不断进行状态转移，最终收敛到平稳分布。

上面概念中的名词解释
1 . 兴趣参数，可以总结我们感兴趣现象的一些数字，通常使用统计学评估参数

2 . 后验分布，这个在概率中已经介绍过。这里在展开一下关于 先验/后验/似然

2-1 . 后验分布–根据结果求原因
举例，已知A花了1个小时到了公园，那么很大可能是他是骑车过去的；如果A花了3个小时才到公园，那么很大可能是他是走过去的；如果A花了1个小时才到公园，那么很大可能是他是开车过去的。

这种预先已知结果（路上花的时间），然后根据结果估计（猜）原因（交通方式）的概率分布即 后验(概率)分布。

2-2 . 先验分布–根据历史求原因
举例，已知A的个人习惯，他是个健身爱好者就喜欢跑步运动，所以我们可以猜测他更可能倾向于走路过去公园。

这里交通工具选择与花费时间不再相关。因为我们是在结果发生前就开始猜的，根据历史规律确定原因 （交通方式）的概率分布即 先验(概率)分布。

2-3 . 似然估计–根据原因求结果
举例，假设到公园10公里
如果A步行走路去，一般情况下小哥大概要用2个多小时。当然很小的可能性是小哥是飞毛腿，跑步过去用了1个小时左右，极为小的可能是小哥是隐藏的高手，10分钟就轻功跑酷到了；
如果A开车去到公园半个小时是非常可能的，非常小的概率是小哥因为途径的路上有车祸堵了3个小时。

这种先定下来原因，根据原因来估计结果的概率分布即 似然估计。根据原因来统计各种可能结果的概率即似然函数。

在贝叶斯学派中，先验分布+数据（似然）= 后验分布 。

3 .马尔可夫链

马尔可夫链是随机建模的强大工具。它是许多著名随机过程之一，包含

• 高斯过程
• 泊松过程
• 自回归模型
• 移动平均模型
• 马尔可夫链

马尔可夫链是一组具有马尔可夫性质的离散随机变量的集合。它研究的是在离散情况下随机的概率。

马尔可夫性质，该性质也被称为“无记忆性（memorylessness）”，即t+1步的随机变量在给定第t步随机变量后与其余的随机变量条件独立（conditionally independent）。简单的说，即过程在t₀时刻所处的状态为已知的条件下，过程在t>t₀时刻所处状态的条件分布与过程在t₀时刻之前所处的状态无关。

看到网上马尔可夫性质的举例，满搞笑的

• 已知你大学学习情况下，和已知你在幼儿园小学初中高中大学的所有学习情况下，考研能不能考上的概率是一样的。
• 已知父母具有某项天赋的条件下，孩子也拥有这个天赋的概率，与已知历代祖先和父母的信息的条件下，孩子拥有这个天赋的概率是一样的。

总结一下：马尔可夫的不追溯当前之前。

马尔可夫链的核心思想是从某个可取任意值的状态$x$出发。 随着时间的推移，我们随机地反复更新状态$x$。最终$x$成为了一个从$p(x)$中抽出的（非常接近）比较一般的样本。

正式的定义中，马尔可夫链由一个随机状态$x$和一个转移分布$T(x’\mid x)$定义而成，$T(x’\mid x)$是一个概率分布，说明了给定状态$x$的情况下随机地转移到$x’$的概率。

运行一个马尔可夫链意味着根据转移分布$T(x’\mid x)$采出的值$x’$来更新状态$x$。

现在回到《机器学习》

在许多实例中，我们希望采用蒙特卡罗方法，然而往往又不存在一种简单的方法可以直接从目标分布$p_{\text{model}}(x)$中精确采样或者一个好的（方差较小的）重要采样分布$q(x)$。

在这种情况下，为了从分布$p_{\text{model}}(x)$中近似采样，我们引入了一种称为马尔可夫链的数学工具。 利用马尔可夫链来进行蒙特卡罗估计的这一类算法被称为马尔可夫链蒙特卡罗方法。

无论状态是连续的还是离散的，所有的马尔可夫链方法都包括重复、随机地更新直到最后状态开始从均衡分布中采样。

我们对新的观察结果进行抽样时，我们会确定它是否在正确的方向，然后决定是保留它还是丢弃它。
两种常见的接受拒绝算法是Metropolis-Hasting算法和No-U-Turn采样器。

运行马尔可夫链直到它达到均衡分布的过程通常被称为马尔可夫链的磨合（Burning-in）过程（下一节中有补充说明）。在马尔可夫链达到均衡分布之后，我们可以从均衡分布中抽取一个无限多数量的样本序列（得到最高的概率值）。

深度学习的从业者们通常选取的马尔可夫链的数目和小批量中的样本数相近，然后从这些固定的马尔可夫链集合中抽取所需要的样本。马尔可夫链的数目通常选为100。

【补充–解释MCMC后验分布过程】
使用 MCMC 方法，我们可以有效地从后验分布中提取样本，然后计算统计特征，例如提取样本的平均值。

首先，MCMC 方法选择一个随机参数值。模拟过程中会持续生成随机的值（即蒙特卡洛部分），但服从某些能生成更好参数值的规则。即对于一对参数值，可以通过给定先验信度计算每个值解释数据的有效性，从而确定哪个值更好。我们会将更好的参数值以及由这个值的解释数据有效性决定的特定概率添加到参数值的链中（即马尔科夫链部分）。

对于单个参数，MCMC 方法会从随机在 x 轴上采样开始。

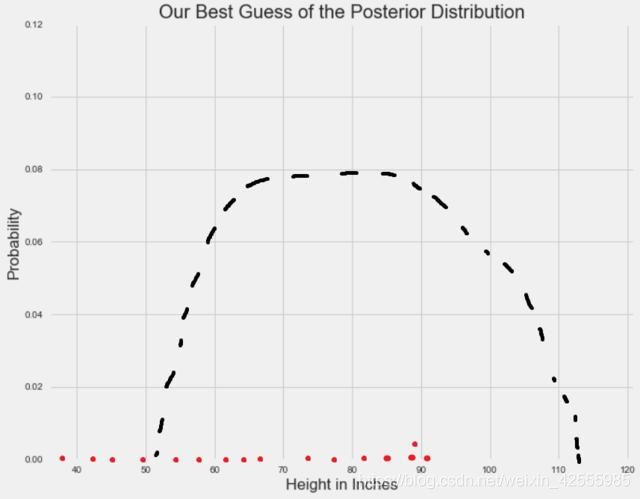
上图中的红点表征随机参数采样。

由于随机采样服从固定的概率，它们倾向于经过一段时间后收敛于参数的高概率区域。

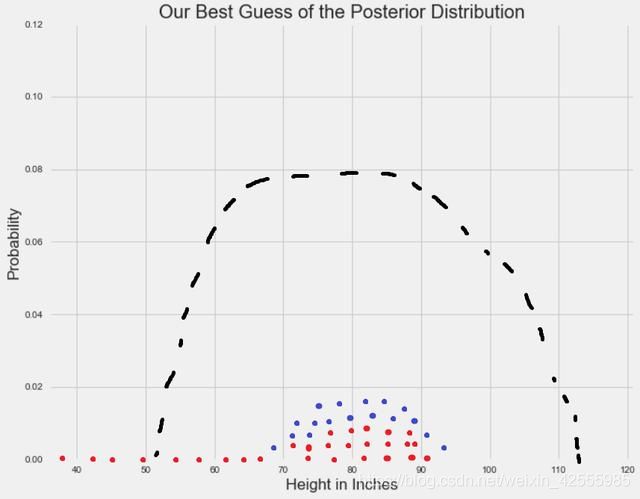
蓝点表示当采样收敛之后，经过任意时间的随机采样。注意：垂直堆叠这些点仅仅是为了说明目的。

收敛出现之后，MCMC 采样会得到作为后验分布样本的一系列点。用这些点画直方图，然后你可以计算任何感兴趣的统计特征。

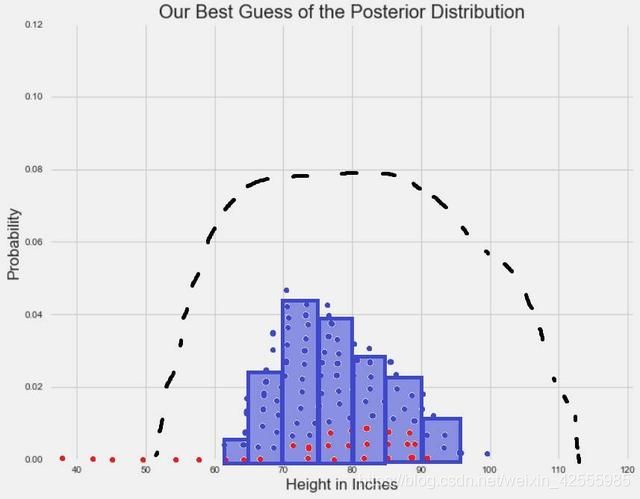
通过 MCMC 模拟生成的样本集合计算的任何统计特征，都是对真实后验分布的统计特征的最佳近似。

MCMC 方法也可以用于评估多于一个参数的后验分布（例如，人类身高和体重）。对于 n 个参数，在 n 维空间中存在高概率的区域，其中特定的参数值集合可以更有效地解释数据。

所以，MCMC 方法的本质，就是在一个概率空间中进行随机采样以近似后验分布，不断磨合，得到最高的概率值。