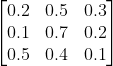马尔可夫链 | 学习笔记

一、什么是马尔可夫链

二、马尔可夫链的核心三要素

1. 状态空间

2. 无记忆性

3. 转移矩阵(转移概率矩阵)

三、稳态的马尔可夫链 

1. 常返性

2. 非周期性

3. 联通性

---

一、什么是马尔可夫链

在机器学习中，马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链（Markov chain），又称离散时间马尔可夫链（discrete-time Markov chain），因俄国数学家安德烈·马尔可夫（俄语：Андрей Андреевич Марков）得名，为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。马尔科夫链作为实际过程的统计模型具有许多应用。

在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点，每一步可以移动到任何一个相邻的点，在这里移动到每一个点的概率都是相同的（无论之前漫步路径是如何的）。

二、马尔可夫链的核心三要素

• 1.状态空间(States Space)
• 2.无记忆性(Memorylessness)
• 3.转移矩阵(Transition Matrix)

1. 状态空间

        状态空间是控制工程中的一个名词。状态是指在系统中可决定系统状态、最小数目变量的有序集合。而所谓状态空间则是指该系统全部可能状态的集合。

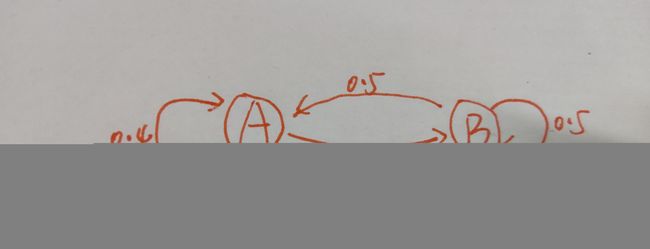
        用一个实例来理解：假设小明第一天购买了早餐A后，第二天再次购买早餐A的概率为0.4，转而去购买早餐B的概率是0.6；第一天购买早餐B后，第二天再次购买早餐B的概率是0.5，转而购买早餐A的概率也是0.5

        那么可以画出该实例的马尔可夫模型为：

        其中早餐A和早餐B为状态空间。

2. 无记忆性

        下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。

        依旧以上述例子为例，小明第N天购买何种早餐只与第N-1天购买的早餐种类有关，而与其他时间节点购买的早餐种类无关。

3. 转移矩阵(转移概率矩阵)

        矩阵各元素都是非负的，并且各行元素之和等于1，各元素用概率表示，在一定条件下是互相转移的，故称为转移概率矩阵。

        上述例子中，转移矩阵为：

        如果小明第一天选择的是早餐A，那么第二天选择的早餐类型的概率为：

                        

         同样的，第三天选择的早餐类型的概率为：

                        

        持续下去，将会得到一个稳态分布，即

 接下来将讨论唯一稳态的马尔可夫链的应用场景和需要满足的条件。

---

三、稳态的马尔可夫链 

首先，马尔可夫链证明：独立性并非均值收敛的必要条件。也就是说，即使非独立的随机过程也能收敛至稳态。

稳态的马尔可夫链的应用范围很广。比如：自然语义处理，即可以更具用户输入的词语推测用户接下来要输入什么，要搜索什么。还能通过稳态的马尔可夫链随机生成诗词、应用于金融行业的熊市与牛市分析等等。

那么什么样的马尔可夫链有唯一的稳态分布呢？

首先假设一个马尔可夫链存在并达到稳态，即：

                

这里的M为转移矩阵，X为当前状态的概率分布。那么可以化解为求M特征值为1的特征向量。

        变换，得到：

                

即求解X得到的稳态分布解。有稳态分布解即说明马尔可夫链能达到稳态。

例如：

        转移矩阵M为：

                

        当前状态state0为

        那么可得state1为，state2为，如此循环下去，可以得到稳态分布为

但是，并非所有的马尔可夫链都有唯一的稳态分布。例如：

状态B和状态C都保持各自的稳态。

如果稳态分布唯一，呢么可根据稳态分布展示出的性质实际应用。比如人们的喜怒哀乐情绪分布；产品选择偏好；金融产品的违约比例，决策者就能制定更有效的策略去影响并改变稳态分布。

那么什么样的马尔可夫链有唯一的稳态分布呢？

直接给出结论：如果马尔可夫链的全部状态节点都满足：

• 1. 常返性(recurrent)
• 2. 非周期性(Aperioddic)
• 3. 连通性

那么该马尔可夫链符合遍历性的要求，即该马尔可夫链能达到唯一稳态。

1. 常返性

        常返性通常与瞬变性(transient)一起理解。若马尔可夫链在到达一个状态后，在演变中能反复回到该状态，则该状态是常返状态，或该马尔可夫链具有（局部）常返性，反之则具有瞬变性的。

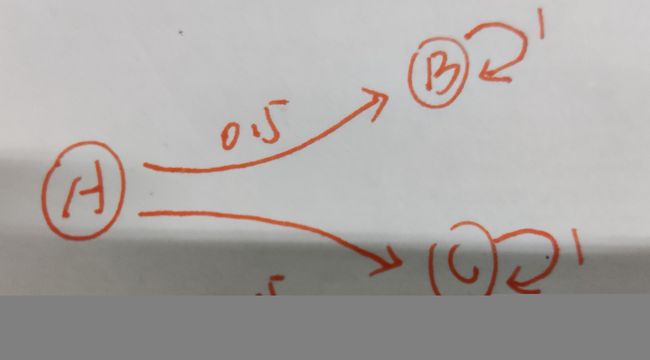
例如一个马尔可夫链为：

        

 B到A，C都有路径，而B，C到A无路径，那么称状态B是瞬变性的，即非常返性。

对A和C来讲，可以进入新状态C或A，并存在路径返回，则认为A，C满足常返性。

2. 非周期性

        一个正常返的马尔可夫链可能具有周期性，即在其演变中，马尔可夫链能够按大于1的周期常返其状态。

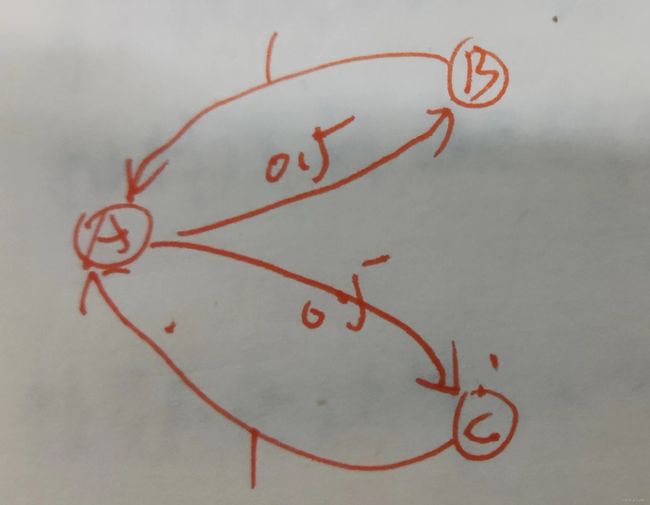
给出下列三个马尔可夫链：

 可以得出各个节点以及节点的周期数分别为：

节点	周期数
A	1,2,3,...N
B	1,2,3,...N
C	1,2,3,...N

节点	周期数
A	3
B	3
C	3

节点	周期数
A	2
B	2,4,6,...,2N
C	2,4,6,...,2N

 马尔可夫链中的某一状态节点，它可以经过K*N个周期返回原点，N为大于等于0的整数，如果K大于等于2，则称该马尔可夫链满足周期性。上述的马尔可夫链中，第一个为非周期性，2，3均为周期性的。

---

3. 联通性

        对于马尔可夫链上任意两个点A和B，假如A能通过相应的路径到达状态B，相反的B也能通过相应的路径达到状态A，那么称马尔可夫链具有连通性