(学习笔记)图像处理——直方图均衡化(HE)
文章目录
-
- 前言
- 原理
- 步骤
- 优缺点
- 改进
-
- 自适应均衡化(AHE)
- 限制对比度的自适应直方图均衡化(CLAHE)
- 实现
前言
利用直方图将图像对比度进行调整,可用来增强局部对比度而对其他部分对比度不受影响。这种方法对于背景和前景都太亮或者太暗的图像非常有用。
直方图:
根据各个灰度级的出现次数绘制成条形图。 如下实例:


原理
假设r( r ≥ 0 r\geq0 r≥0)和s( s ≤ 1 s\leq1 s≤1)分别表示归一化的原图像灰度和通过直方图均衡化后的图像灰度,对于每一个r,灰度变换函数 T ( r ) T(r) T(r)都可以产生一个对应的s,即: s = T ( r ) s=T(r) s=T(r),其满足以下两个条件:
- 在 0 ≤ r ≤ 1 0\leq r\leq 1 0≤r≤1内, T ( r ) T(r) T(r)为单调递增函数;
- 在 0 ≤ r ≤ 1 0\leq r\leq 1 0≤r≤1内,有 0 ≤ T ( r ) ≤ 1 0\leq T(r)\leq1 0≤T(r)≤1。
s所对应的分布函数为:
F s ( s ) = ∫ − ∞ s P s ( s ) d s = ∫ − ∞ r P r ( r ) d r F_{s}(s)=\int_{-\infty}^{s}{P_{s}(s)}ds=\int_{-\infty}^{r}{P_{r}(r)}dr Fs(s)=∫−∞sPs(s)ds=∫−∞rPr(r)dr
其中, P s ( s ) {P_{s}(s)} Ps(s)为均衡化之后图像灰度的概率密度函数, P r ( r ) P_{r}(r) Pr(r)为原图像灰度的概率密度函数。
对上式两边求导可得:
P s ( s ) = d F s ( s ) d s = P r ( r ) d r d s = P r ( r ) d r d [ T ( r ) ] P_{s}(s)=\frac{dF_{s}(s)}{ds}=P_{r}(r)\frac{dr}{ds}=P_{r}(r)\frac{dr}{d[T(r)]} Ps(s)=dsdFs(s)=Pr(r)dsdr=Pr(r)d[T(r)]dr
由此可以看出通过灰度变换函数 T ( r ) T(r) T(r)可以控制灰度概率密度函数 P s ( s ) P_{s}(s) Ps(s),从而改善图像的灰度层次。
灰度变换函数的确定:
直方图均衡化的最终目的是获得灰度均匀分布的图像,因此均衡化之后的直方图的 P s ( s ) P_{s}(s) Ps(s)应当是均匀分布的概率密度函数,即 P s ( s ) = 1 P_{s}(s)=1 Ps(s)=1。对上式积分可得:
s = T ( r ) = ∫ 0 r P r ( r ) d r s=T(r)=\int_{0}^{r}P_{r}(r)dr s=T(r)=∫0rPr(r)dr
灰度级为离散的数字图像时,其灰度变换函数为:
s k = T ( r k ) = ∑ i = 0 k p r ( r i ) = ∑ i = 0 k n i N s_{k}=T(r_{k})=\sum_{i=0}^{k}{p_{r}(r_{i})}=\sum_{i=0}^{k}{\frac{n_{i}}{N}} sk=T(rk)=i=0∑kpr(ri)=i=0∑kNni
其中, 0 ≤ r k ≤ 1 ( k = 0 , 1 , 2 , ⋯ , L − 1 ) 0\leq r_{k}\leq1(k=0,1,2,\cdots,L-1) 0≤rk≤1(k=0,1,2,⋯,L−1), r k = k / ( L − 1 ) r_{k}=k/(L-1) rk=k/(L−1),L-1表示没有归一化的原图像的灰度最大值; n i n_{i} ni为原图像中第 i i i个灰度级的像素出现的次数;N为原图像中像素点的总数。
对于灰度分布在[0,L-1]的灰度图像,只需将上式乘以灰度的最大值L-1即可:
s k = T ( r k ) = ∑ i = 0 k p r ( r i ) × ( L − 1 ) = ∑ i = 0 k n i N × ( L − 1 ) s_{k}=T(r_{k})=\sum_{i=0}^{k}{p_{r}(r_{i})}\times(L-1)=\sum_{i=0}^{k}{\frac{n_{i}}{N}}\times(L-1) sk=T(rk)=i=0∑kpr(ri)×(L−1)=i=0∑kNni×(L−1)
步骤
第一步:统计每个灰度级的像素个数并绘制直方图;
第二步:计算新的灰度级;
第三步:修正 s k s_{k} sk为合理的灰度级;
第四步:计算新的直方图;
第五步:用处理后的新灰度代替处理前的灰度,生成新图像。
优缺点
优点: 直观可视化换技术;可进行逆操作,如果已知均衡化函数,便可以恢复原始的直方图。
缺点: 没有考虑局部图像区域,只是将整体均衡化,所以会由于整体亮度的提升使得局部图像的细节变得模糊。
对彩色图像均衡化采用三通道分别进行均衡化然后再合成的方法。还有一种方法是先把RGB转换为HSV,然后再均衡化。
改进
自适应均衡化(AHE)
对于在直方图均衡化的缺点衍生出了自适应均衡化的方法,其主要思想是在均衡化过程中将图像分为若干子块,对每个子块进行直方图均衡化处理,只利用局部区域窗口内的直方图分布构建映射函数,因此更适合改进图像局部对比度以获得更多的图像细节。
优点: 图像的灰度值较好地分布在了全部动态范围上,局部对比度得到了提升,视觉效果优于直方图均衡化。
缺点: 局部对比度提高过大会导致图像失真,还会放大图像中的噪声。
限制对比度的自适应直方图均衡化(CLAHE)
对于自适应直方图均衡化产生的对比度过大和不连续等缺点,衍生出该方法,其改进在于:
限制直方图分布:
对于原图像的直方图设定一个阈值,对超过阈值的灰度级进行裁剪,然后将超出阈值的部分平均分配到各个灰度级,将使得映射函数的结果较为平缓。其步骤如下:
第一步:对图像进行分块;
第二步:计算每个子块的直方图;
第三步:计算裁剪阈值;
第四步:对裁剪之后多余的像素点进行重新分配;
第五步:直方图均衡;
第六步:像素点灰度值重构。
插值:
将图像进行分块处理后会导致最终图像呈现块状,不连续的情况。所以引入插值方法。

注:图片来源百度搜索
其处理步骤为:
第一步:将图像分成均等大小的等份矩形块,如图中右侧所示;
第二步:计算每个块的直方图,变换函数,这些对于图左侧中的小黑块是符合的,其在分块的中心位置;
第三步:对于边缘的绿色阴影部分采用线性插值求出像素值:
f ( x , y ) = x 2 − x x 2 − x 1 f 1 + x − x 1 x 2 − x 1 f 2 f(x,y)=\frac{x_{2}-x}{x_{2}-x_{1}}f_{1}+\frac{x-x_{1}}{x_{2}-x_{1}}f_{2} f(x,y)=x2−x1x2−xf1+x2−x1x−x1f2
其中, f ( x , y ) f(x,y) f(x,y)表示所求像素点的值,相邻像素块中心坐标分别为 ( x 1 , y 1 ) (x_{1},y_{1}) (x1,y1)和 ( x 2 , y 2 ) (x_{2},y_{2}) (x2,y2),相邻块的映射值分别为 f 1 f_{1} f1和 f 2 f_{2} f2。
第四步:对于中间的紫色阴影部分采用双线性插值求出像素值:
f ( x , y ) = ( x 2 − x ) ( y 2 − y ) ( x 2 − x 1 ) ( y 2 − y 1 ) f 1 + ( x − x 1 ) ( y 2 − y ) ( x 2 − x 1 ) ( y 2 − y 1 ) f 2 + ( x 2 − x ) ( y − y 1 ) ( x 2 − x 1 ) ( y 2 − y 1 ) f 3 + ( x − x 1 ) ( y − y 1 ) ( x 2 − x 1 ) ( y 2 − y 1 ) f 4 f(x,y)=\frac{(x_{2}-x)(y_{2}-y)}{(x_{2}-x_{1})(y_{2}-y_{1})}f_{1}+\frac{(x-x_{1})(y_{2}-y)}{(x_{2}-x_{1})(y_{2}-y_{1})}f_{2}+\frac{(x_{2}-x)(y-y_{1})}{(x_{2}-x_{1})(y_{2}-y_{1})}f_{3}+\frac{(x-x_{1})(y-y_{1})}{(x_{2}-x_{1})(y_{2}-y_{1})}f_{4} f(x,y)=(x2−x1)(y2−y1)(x2−x)(y2−y)f1+(x2−x1)(y2−y1)(x−x1)(y2−y)f2+(x2−x1)(y2−y1)(x2−x)(y−y1)f3+(x2−x1)(y2−y1)(x−x1)(y−y1)f4
其中, f 1 , f 2 , f 3 , f 4 f_{1},f_{2},f_{3},f_{4} f1,f2,f3,f4为四个像素块的映射值,四个块的中心坐标分别为 ( x 1 , y 1 ) , ( x 1 , y 2 ) , ( x 2 , y 1 ) , ( x 2 , y 2 ) (x_{1},y_{1}),(x_{1},y_{2}),(x_{2},y_{1}),(x_{2},y_{2}) (x1,y1),(x1,y2),(x2,y1),(x2,y2)
第五步:对于边角的粉色阴影部分直接进行映射函数计算;
第六步:得到新的直方图,用新灰度代替处理前的灰度,生成新图像。
实现
HE:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
from skimage.metrics import peak_signal_noise_ratio
from skimage.metrics import structural_similarity
import csv
def equalizeHist(image):
B, G, R = cv.split(image) # 多通道分解为单通道图像
# #直方图均衡化
EB = cv.equalizeHist(B)
EG = cv.equalizeHist(G)
ER = cv.equalizeHist(R)
equal_test = cv.merge((EB, EG, ER)) # 单通道合成为多通道图像
# 计算直方图
hist_EB = cv.calcHist([EB], [0], None, [256], [0, 256])
hist_EG = cv.calcHist([EG], [0], None, [256], [0, 256])
hist_ER = cv.calcHist([ER], [0], None, [256], [0, 256])
hist_b = cv.calcHist([B], [0], None, [256], [0, 256])
plt.plot(hist_EB, 'b'); #展示均衡化之后B通道的直方图
plt.show()
plt.plot(hist_b, 'r'); #展示原始B通道直方图
plt.show()
return equal_test
##存储数据
def writeCsv(image, psnr, ssim):
row = [image, psnr, ssim]
out = open("D:/Histogram equalization/result.csv", "a", newline="")
csv_writer = csv.writer(out, dialect="excel")
csv_writer.writerow(row)
writeCsv("image", "psnr", "ssim")
for j in range(0, 10):
test = cv.imread("D:/Histogram equalization/Infrared_image/000{}.jpg".format(str(j)))
print(f"000{j}.jpg:")
equal_test = equalizeHist(test)
#cv.imshow("test", test)
#cv.imshow("equal_test", equal_test)
cv.imwrite("D:/Histogram equalization/result_image/000{}.jpg".format(str(j)), equal_test)
key = cv.waitKey(0)
cv.destroyAllWindows()
# 计算psnr
psnr = peak_signal_noise_ratio(test, equal_test)
# 计算ssim
img_1 = cv.cvtColor(test, cv.COLOR_BGR2GRAY) # 由于img彩色图片,而img_new是灰度图像,所以计算psnr和ssim之前需要将img转化为灰度图片
equal = cv.cvtColor(equal_test, cv.COLOR_BGR2GRAY)
ssim = structural_similarity(img_1, equal)
print(f"psnr={psnr}")
print(f"ssim={ssim}")
writeCsv(j, psnr, ssim)
输入图像:

原始图像B通道直方图:

均衡化之后B通道直方图:
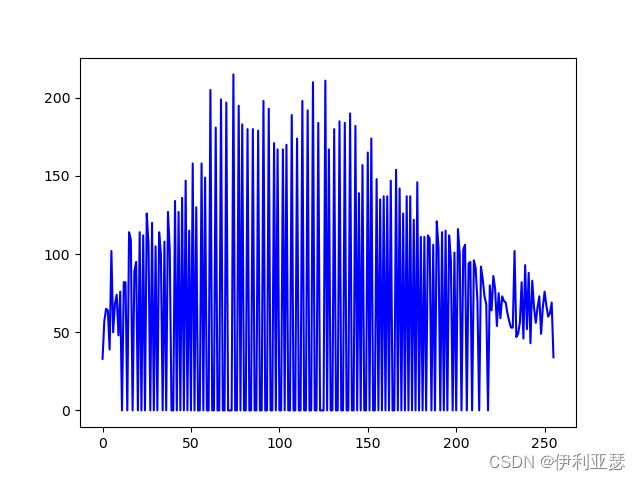
原始图像G通道直方图:
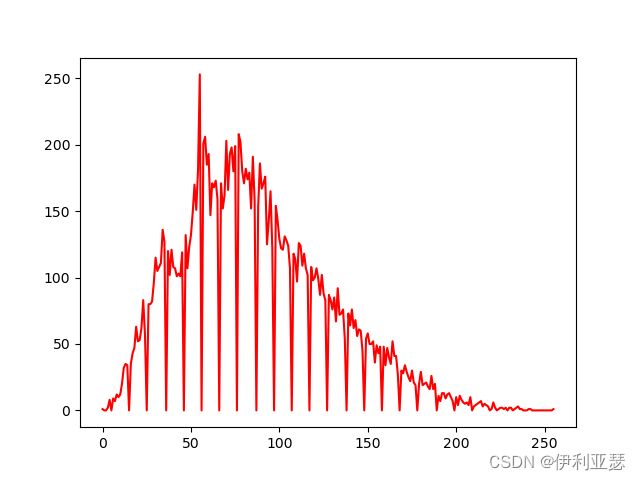
均衡化之后G通道直方图:

原始图像R通道直方图:

均衡化之后R通道直方图:

直方图均衡化之后的图像:

对应psnr和ssim:

CLAHE:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
from skimage.metrics import peak_signal_noise_ratio
from skimage.metrics import structural_similarity
import csv
def hisEqulColor2(img):
B, G, R=cv.split(img)
clahe=cv.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
b = clahe.apply(B)
g = clahe.apply(G)
r = clahe.apply(R)
hist_B = cv.calcHist([B], [0], None, [256], [0, 256])
hist_b = cv.calcHist([b], [0], None, [256], [0, 256])
plt.plot(hist_B, 'r')
plt.plot(hist_b, 'b')
plt.show()
hist_G = cv.calcHist([G], [0], None, [256], [0, 256])
hist_g = cv.calcHist([g], [0], None, [256], [0, 256])
plt.plot(hist_G, 'r')
plt.plot(hist_g, 'b')
plt.show()
hist_R = cv.calcHist([R], [0], None, [256], [0, 256])
hist_r = cv.calcHist([r], [0], None, [256], [0, 256])
plt.plot(hist_R, 'r')
plt.plot(hist_r, 'b')
plt.show()
image = cv.merge((b, g, r))
#cv.cvtColor(ycrcb, cv.COLOR_YCR_CB2BGR, img)
return image
##存储数据
def writeCsv(image, psnr, ssim):
row = [image, psnr, ssim]
out = open("D:/Histogram equalization/自适应直方图均衡化/result.csv", "a", newline="")
csv_writer = csv.writer(out, dialect="excel")
csv_writer.writerow(row)
#writeCsv("image", "psnr", "ssim")
for j in range(1, 2):
test = cv.imread("D:/Histogram equalization/Infrared_image/000{}.jpg".format(str(j)))
print(f"000{j}.jpg:")
equal_test = hisEqulColor2(test)
cv.imshow("test", test)
cv.imshow("equal_test", equal_test)
cv.imwrite("D:/Histogram equalization/自适应直方图均衡化/result_image/000{}.jpg".format(str(j)), equal_test)
key = cv.waitKey(0)
cv.destroyAllWindows()
img_1 = cv.cvtColor(test, cv.COLOR_BGR2GRAY) # 由于img彩色图片,而img_new是灰度图像,所以计算psnr和ssim之前需要将img转化为灰度图片
equal = cv.cvtColor(equal_test, cv.COLOR_BGR2GRAY)
# 计算psnr
psnr = peak_signal_noise_ratio(img_1, equal)
# 计算ssim
ssim = structural_similarity(img_1, equal)
print(f"psnr={psnr}")
print(f"ssim={ssim}")
writeCsv(j, psnr, ssim)
输入图像同HE。
B通道均衡化前后直方图:
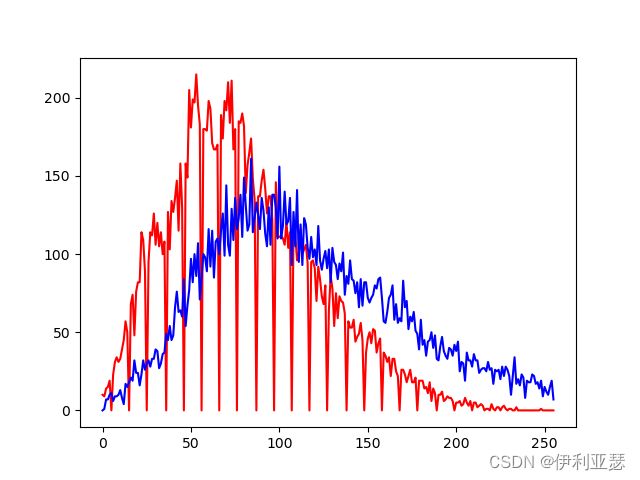
G通道均衡化前后直方图:
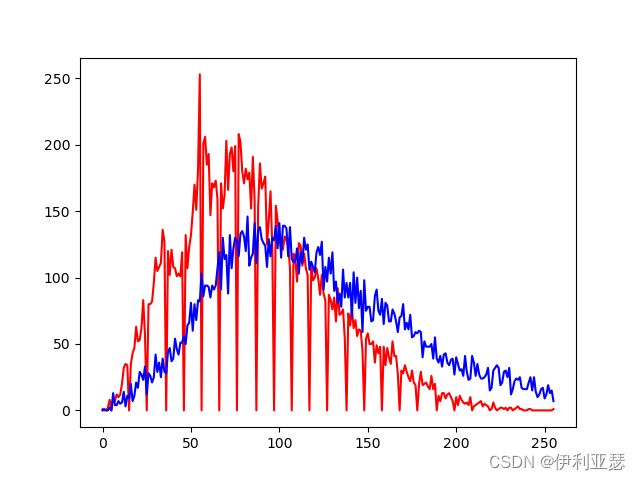
R通道均衡化前后直方图:

CLAHE之后的图像:

对应的psnr及ssim如下:

个人学习笔记分享,错误望请指正!