【Kaggle学习】Intro to Deep Learning

一个小白的学习记录

官方网站：link
知乎：link，在我不会翻译的时候会参考这个，他翻译的比较通顺，我这个主要作为一个记录学习过程。

A Single Neuron

Learn about linear units, the building blocks of deep learning.

什么是深度学习

深度学习是一种以深度计算为特征的机器学习方法。这种计算深度使深度学习模型能够理清在复杂数据集中发现的各种复杂模式。

神经网络(neural networks)由于其强大的功能和可扩展性，已经成为深度学习的定义模型。神经网络由神经元组成，每个神经元单独执行一个简单的计算。相反，神经网络的力量来自于这些神经元复杂的连接。

线性单位

从神经网络最基本的单个神经元（单位）开始。

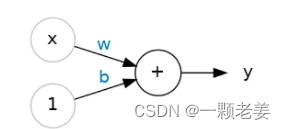
x是输入(input)，w是权重(weight)，b是偏差(bias)。
w:神经网络通过修改其权重来“学习”。
b:这种偏差使神经元能够独立于其输入修改输出。
(A neural network “learns” by modifying its weights.)

Example - The Linear Unit as a Model

以“糖”作为“输入”，“卡路里”作为“输出”建立单个神经元，通过线性单位计算得到w=2.5，b=90。

（数据集：link）

Example - Multiple Inputs

如果自变量不止一个，例如在上个数据集中不只有“糖”，还有其他的字段。在一个神经元中，将不同“输入”与他们对应的w值相乘后的结果相加，从而得到“输出”值。

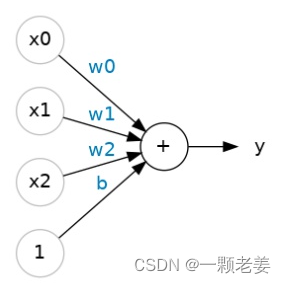
=00+11+22+ .

（A linear unit with two inputs will fit a plane, and a unit with more inputs than that will fit a hyperplane.
一个具有两个输入的线性单元将适合一个平面，而一个具有更多输入的单元将适合超平面。）

Example - Multiple Inputs

keras.Sequential可以用来建立一个神经元。它将神经网络创建为层堆栈（a stack of layers）。我们可以使用密集层（dense layer）（我们将在下一节中了解更多信息）来创建与上述类似的模型。

我们可以定义一个线性模型，接受三个输入特征（“糖”、“纤维”和“蛋白质”）并产生一个输出（“卡路里”），如下所示：

from tensorflow import keras
from tensorflow.keras import layers

# Create a network with 1 linear unit
model = keras.Sequential([layers.Dense(units=1, input_shape=[3])])

其中，units= n 表示有n个“输出”。这里只有一个“卡路里”，units设置为1。
input_shape=[m] 表示有m个“输入”。这里有“糖”、“纤维”和“蛋白质”三个，input_shape=[3]。

Deep Neural Networks

Add hidden layers to your network to uncover complex relationships.

We’ve seen how a linear unit computes a linear function – now we’ll see how to combine and modify these single units to model more complex relationships.

Layers

神经网络通常将它们的神经元组织成层。当我们将具有一组公共输入的线性单元收集在一起时，我们会得到一个密集层(dense layer)。

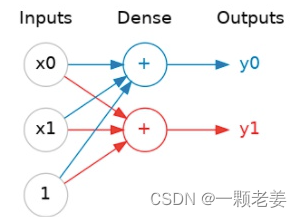
可以将神经网络中的每一层（layer）看作是执行某种相对简单的转换。通过层层叠加，神经网络可以将“输入”以更复杂的方式转换。在一个被训练的神经网络中，每层的转换都会进一步向目标结果迈进。

Many Kinds of Layers
A “layer” in Keras is a very general kind of thing. A layer can be, essentially, any kind of data transformation. Many layers, like the convolutional and recurrent layers, transform data through use of neurons and differ primarily in the pattern of connections they form. Others though are used for feature engineering or just simple arithmetic. There’s a whole world of layers to discover – check them out!

The Activation Function

两个密集层中间没有任何连接的话，其效果不一定优于一个密集层，密集层本身永远无法将我们移出线和平面的世界。而我们所需要的非线性的，我们需要的是激活函数（Activation functions）

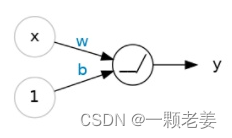
激活函数应用于每个层的输出（its activations）。最常见的是整流函数（rectifier function） (0,) 。

整流函数的图表是负数部分为0的线性函数。整流函数应用在神经元的输出数据，可以使数据弯曲，使我们远离简单的线性。

当我们将整流器作用于线性单元时，可以得到一个线性整流单元（rectified linear unit）或者称之为ReLU（由于这个原因，整流函数也常被称作“ReLU 函数”）。ReLU 作用在一个线性单元意味着其输出变成了max(0, w * x + b)，图形如下：

Stacking Dense Layers

现在我们有了一些非线性的结果，让我们看看如何堆叠这些层来得到更复杂的数据转换。

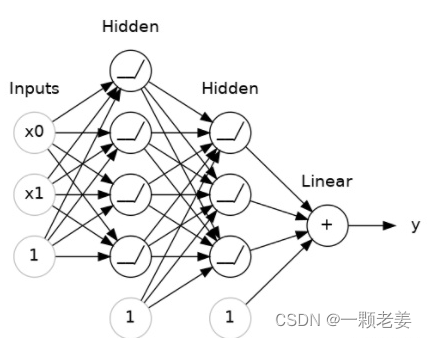
在输出层之前层的被称为隐藏层（hidden layer），因为我们无法直接看到这些层的输出结果。

最终层是一个线性单元（也就是没有激活函数）。这使得这个神经网络适用于一些试图去预测任意数值的回归分析。其他的任务（例如分类）可能需要输出的激活函数。

Building Sequential Models

我们一直用Sequential模型来将一系列层按照从前到后的顺序连接在一起。第一层获取输入，最后一层产生输出：

from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
    # the hidden ReLU layers
    layers.Dense(units=4, activation='relu', input_shape=[2]),
    layers.Dense(units=3, activation='relu'),
    # the linear output layer 
    layers.Dense(units=1),])

确保将所有层一起传递到列表中，而不是分开传递。如果要在某层中加入一个激活函数，只需在激活参数中指定其名称。

Stochastic Gradient Descent

Use Keras and Tensorflow to train your first neural network.

Introduction

在前两节课中，我们学习了如何从密集层(dense)的堆栈中构建完全连接的网络。当第一次创建神经网络时，网络中的权重（weights）都是随机的，神经网络还不知道任何信息。在这一届中， 我们将学习如何训练神将网络以及他是如何学习的。

在所有机器学习任务中，我们从准备训练数据开始。在每一个训练数据的例子中，均由一些特征（the input）和一个期望目标（the output）构成。训练神经网络就是以一定方式调整权重使这些特征可以转化为期望目标。如，在 80 Cereals 数据集中，我们想让神经网络考虑每种谷物的’sugar’, ‘fiber’ 和 ‘protein’ 的含量并据此预测每种谷物的’calories’。如果我们能够成功地训练一个网络，那么它的权重必须以某种方式表示这些特征与训练数据中表示的目标之间的关系。

除了训练数据，我们还需要两件事：

• 损失函数（loss function）来计算神经网络预测结果的好坏；
• 一个“优化器”，可以告诉网络如何改变它的权重。

The Loss Function

我们已经知道如何设计一个神经网络的结构，但是我们还不清楚如何告诉一个神经网络我们要解决什么问题。这就是损失函数的作用。

损失函数测量计算真实值和模型预测值之间的差异。

不同的问题需要不同的损失函数。一个常见的回归问题的损失函数是“平均绝对误差”（mean absolute error）（MAE）。对每个预测的y值（y_pred），平均绝对误差是真实y值（y_true）和y_pred之间的差距的绝对值：abs(y_true-y_pred)。

数据集上的总 MAE 损失是所有这些绝对差异的平均值。

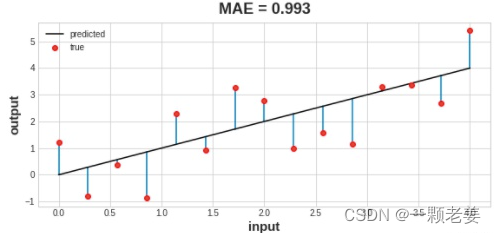
除了MEA，回归问题中可能用到的损失函数还有均方误差（mean-squared error，MSE）、 Huber loss （这两个损失函数都在Keras可用）。

在训练期间，模型用损失函数来作为找到它权重正确数值的指南（损失越小越好）。换句话说，损失函数在告诉神经网络他的目标。

The Optimizer - Stochastic Gradient Descent

以上已经告诉了神经网络它要解决的目标，但现在我们需要知道如何解决它。这是优化器的工作。优化器是一种调整权重以最小化损失的算法。

实际上，在深度学习中所有用到的优化器算法都属于随机梯度下降（stochastic gradient descent）。他们是用迭代算法逐步训练模型。模型训练每一步的目标是：

• 采样一些训练数据，并通过网络进行预测。
• 计算真实数据和预测数据之间的损身。
• 最终，调整权重方向使其损失降低。

然后，重复进行这些步骤知道损失到达我们可接受的范围（或者知道它的损失不再降低）。

每次迭代的训练数据样本称为小批量（minibatch或者“batch”），而完整的一轮训练数据称为一个周期（epoch）。训练的周期数是网络模型将看到每个训练示例的次数。

Learning Rate and Batch Size

线只在每个批次的方向上有小幅移动（而不是一直移动）。移动的大小就是学习速率（learning rate）。训练速度小意味着要达到模型最优需要很多批次来调整他的权重。

学习速率和批次的大小是对影响SGD训练进程影响最大的两个因素。它们的相互作用通常是微妙的，这些参数的正确选择并不总是显而易见的。

幸运的是，大多数工作不需要进行大量的超参数搜索来获得满意的结果。Adam是SGD算法的一种，具有自适应学习率，它可以适用于大多数问题而无需任何参数调整（从某种意义上说，它是“自调整”）。 Adam 是一个很棒的通用优化器。

Adding the Loss and Optimizer

在定义了一个模型后，可以在模型编译中加入一个损失函数和优化器

model.compile(
    optimizer="adam",
    loss="mae",)

请注意，我们可以仅用一个字符串来指定损失和优化器。更多的可选参数，可以查看 Keras API 。

What’s In a Name?
The gradient is a vector that tells us in what direction the weights need to go. More precisely, it tells us how to change the weights to make the loss change fastest. We call our process gradient descent because it uses the gradient to descend the loss curve towards a minimum. Stochastic means “determined by chance.” Our training is stochastic because the minibatches are random samples from the dataset. And that’s why it’s called SGD!

Example - Red Wine Quality

这个数据集包括1600种葡萄牙红酒的物化测量值。也包括每种酒盲测的质量评价。我们如何通过这些测量值预测酒的品质？

首先导入数据，并进行归一化（数据在[0-1]范围内）。

import pandas as pd
from IPython.display import display

red_wine = pd.read_csv('../input/dl-course-data/red-wine.csv')

# Create training and validation splits
df_train = red_wine.sample(frac=0.7, random_state=0)
df_valid = red_wine.drop(df_train.index)
display(df_train.head(4))

# Scale to [0, 1]
max_ = df_train.max(axis=0)
min_ = df_train.min(axis=0)
df_train = (df_train - min_) / (max_ - min_)
df_valid = (df_valid - min_) / (max_ - min_)

# Split features and target
X_train = df_train.drop('quality', axis=1)
X_valid = df_valid.drop('quality', axis=1)
y_train = df_train['quality']
y_valid = df_valid['quality']

查看有多少输入数据，可以通过查找数据矩阵有多少列。

print(X_train.shape)

11列代表有11个输入数据。

这里选择三层神经网络包含超过1500个神经元。这个神经网络中数据的复杂程度可以满足训练目标的要求。

from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
    layers.Dense(512, activation='relu', input_shape=[11]),
    layers.Dense(512, activation='relu'),
    layers.Dense(512, activation='relu'),
    layers.Dense(1),
])

定义模型后，编译选择器和损失函数

model.compile(
    optimizer='adam',
    loss='mae',
)

现在准备开始训练！以 256的批量大小训练网络 10个 epoch。

history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=256,
    epochs=10,
)

通常，通过做散点图来更好的查看损失变化。

import pandas as pd

# convert the training history to a dataframe
history_df = pd.DataFrame(history.history)
# use Pandas native plot method
history_df['loss'].plot();

对于学习速率和批次大小，可以控制：

• 训练模型的时间
• 学习曲线的噪音
• 损失达到多小

Overfitting and Underfitting

Keras 能保留它训练模型过程中训练和验证损失的历史记录，并且可以画出来。这节课要学习如何解释这些学习曲线以及我们如何用他们去引导模型发展。

Interpreting the Learning Curves

我们认为训练数据的信息有两种：信号（Signal）和噪音（noise）。信号是概括，可以帮助我们的模型从新数据中预测结果。噪声只适用于被训练的数据，噪声是来自现实世界中的数据的所有随机波动，或者是所有无法实际帮助模型做出预测的偶然的、非信息性的模式。噪音是部分可能看起来有用但实际上不是。

我们通过选择权重或者在训练设置中设置使损失最小的参数来训练模型。但是，最终对一个模型准确性评估，需要在一个新的数据集上（验证数据集：the validation data）来评价。

当我们训练一个模型时，会逐个周期的画出训练时的损失，为了这个，也会加入绘制验证数据集。这些图我们叫它学习曲线（learning curves）。为了有效的训练深度模型，我们需要解释他。

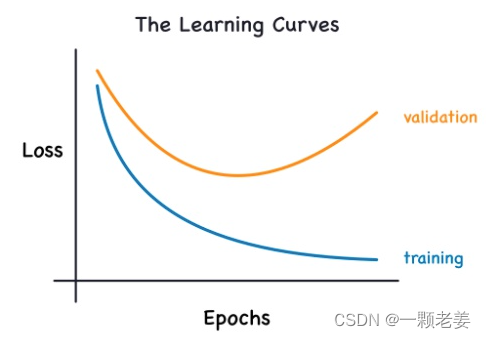
现在，无论模型学习的是信号还是噪音，训练损失都会下降。但是验证损失只会在模型训练信号时下降（模型从训练集中学到的任何噪声都不会推广到新数据）。所以，当一个模型学习信号时曲线会下降，但是当他学习噪声时两个曲线就会有差异，这个差异的大小就表明有这个模型已经学习了多少噪声。

理想中，我们能够穿件一个只学习信号不学习噪声的模型，实际上这永远不会发生。我们会进行权衡。我们要让模型学习更多的信号就要以学习更多的噪声为代价。只要这种权衡让我们有利，验证损失就会下降。然而，达到特定点后，这种权衡转向对我们不利，花费超过收益，验证损失开始升高。

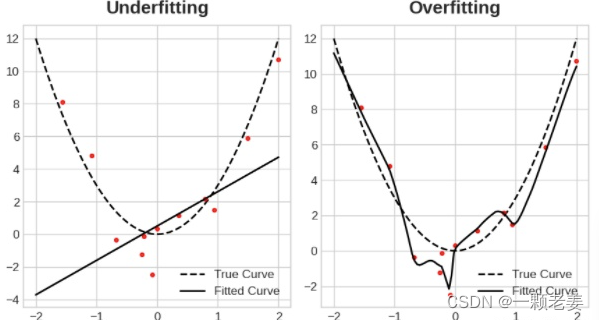
这种权衡表明在训练模型时会出现两种问题：信号数据不够或者噪音太多。欠拟合（Underfitting）训练集时因为模型没有学习足够多的信号而使损失不够低。过拟合（overfitting）训练集时由于学习了太多噪声，而使损失不够低。训练深度学习磨心高的技巧就是找到两者的最佳平衡。

我们看看几种在数据集中获取更多信号或者减少大量噪声的方法。

Capacity

模型Capacity是指它能学习的图案的大小和复杂性。对于神经网络，主要受有多少神经元和他们的连接方式的共同影响。如果你的神经网络出现数据过拟合，你需要试着增加他的capacity。

你可以通过拓宽（wider，更多存在的层上添加更多单元）或者深挖（deeper，增添更多层）来增加capacity。越宽的网络越容易学习到更多的线性关系，而越深的网络更倾向于学习非线性关系。哪个更好只取决于数据集。

model = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(1),
])

wider = keras.Sequential([
    layers.Dense(32, activation='relu'),
    layers.Dense(1),
])

deeper = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(16, activation='relu'),
    layers.Dense(1),
])

Early Stopping

我们提到，当模型过于急切地学习噪声时，验证损失可能会在训练期间开始增加。为了防止此事，当模型的验证损失不再下降时我们就终止训练。这种打断训练方式叫做早停法（early stopping）。

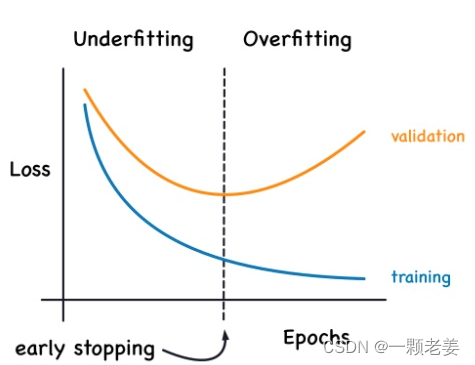
一旦我们发现验证损失开始复升，我们需要重新将权重值设置为验证损失最小时的权重值。确保模型不再继续学习噪声造成数据过拟合。

训练模型使用早停法意味着我们不太可能在网络完成学习信号之前过早停止训练。所以出了防止由于训练过长导致的过拟合，提前停止还可以防止欠拟合训练时间不够长。只需将您的训练时期设置为一个较大的数字（比您需要的多），早期停止将处理其余部分。

Adding Early Stopping

在 Keras 中，我们利用回调函数(callback)将early stopping包含在我们的训练过程中。回调函数只是您希望在网络训练时经常运行的函数。early stopping callback 将在每个 epoch 之后运行。 （Keras 预定义了各种有用的回调，但您也可以定义自己的回调。）

from tensorflow.keras.callbacks import EarlyStopping

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

这些参数表示：在之前20个周期里验证损失没有达到至少下降0.001，那么训练停止并且你找到了最佳模型。有时很难判断验证损失是由于过度拟合还是仅仅由于随机批次变化而上升。这些参数允许我们设置一些关于何时停止的余量。

Overfitting and Underfitting

Add these special layers to prevent overfitting and stabilize training.

Introduction

在深度学习的世界里不仅只有密集层，而是有数十种层可以加入到模型中。有些类似于dense层并定义神经元之间的连接，而有些则可以进行其他类型的预处理或转换。

本节课中，我们会学习两种特殊类型的层，他们本身不包含神经元，但是添加了一些功能，这些功能有时以各种方式让模型受益。这两种都在现代结构里很常见。

Dropout

第一种是“dropout layer”（dropout层），他可以矫正过拟合。

在上一篇文章中，我们讨论了网络学习训练数据中的虚假模式如何导致过度拟合。为了认清一个神经网络的这些虚假模式，经常需要一个特殊的权重结合，一种权重的“阴谋”。他如此特殊，他们是脆弱的：删除一个，整个“阴谋”就会瓦解。

这就是 dropout 背后的想法。为了打破这些阴谋，我们在训练的每一步都随机丢弃一层的输入单元的一部分，为神经网络从这些训练数据中学习虚假模式增加困难。相反的，他可以寻找宽阔的、通用的模式，这些权重组合更加稳健。

为了打破这些阴谋，我们在训练的每一步随机丢弃层输入单元的一部分，使网络更难学习训练数据中的那些虚假模式。相反，它必须搜索广泛的、通用的模式，其权重模式往往更加稳健。

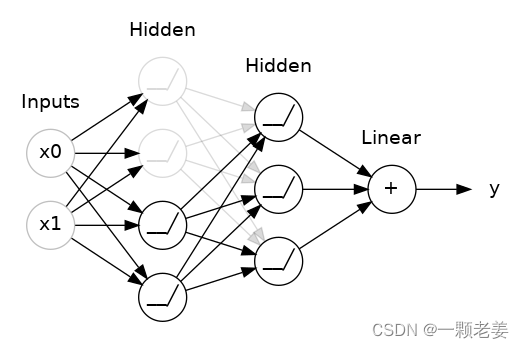
你可以将dropout看作一种和谐的神经网络。预测将不再是需要建立一个大的神经网络，而是一个小神经网络的“committee”。独立的committee网络网有不同的错误，但是同时又是对的，使得committee看作一个整体时比独立时要好。（如果你熟悉作为决策树集合的随机森林，这两个是同样想法。）

Adding Dropout

在Keras，dropout的参数rate是要关闭的输入单元的百分比。将Dropout层放在你想要dropout作用的层之前：

keras.Sequential([
    # ...
    layers.Dropout(rate=0.3), # apply 30% dropout to the next layer
    layers.Dense(16),
    # ...
])

Batch Normalization

另一个特殊的层是“batch normalization”（或者“batchnorm”），这有助于纠正缓慢或不稳定的训练。

对于神经网络，通常是将所有数据缩放到一个共同的尺度上，可以使用 scikit-learn 中的 StandardScaler 或 MinMaxScaler 之类的方法。原因是，SGD将根据数据产生的激活量，按比例改变网络权重。倾向于产生非常不同大小的激活的特征会导致不稳定的训练行为。

现在，如果数据在他输入神经网络之前就标准化是好的，那夜戏在神经网络中将数据标准化可能更好！实际上，又闷又一种特殊的层可以做到，就是“batch normalization layer”。 一个batch normalization layer 会在每个批次(batch)进来时查看它，首先用它自己的均值和标准差对批次进行归一化，然后还使用两个可训练的重新缩放参数将数据放在一个新的尺度上。实际上，Batchnorm 对其输入进行了一种协调的重新缩放。

在大多数情况下，被看作是优化过程的辅助工具（尽管它有时也有助于预测性能）。具有batchnorm的模型往往需要更少的 epoch 来完成训练。此外，batchnorm 还可以解决可能导致训练“卡住”的各种问题。考虑为模型添加批量归一化，尤其是当在训练过程中遇到问题时。

Adding Batch Normalization

似乎batch nomalization可以用在神经网络大部分地方。你能够将它放在一个层之后。

layers.Dense(16, activation='relu'),
layers.BatchNormalization(),

或者一个层和他的激活函数之间：

layers.Dense(16),
layers.BatchNormalization(),
layers.Activation('relu'),

如果你在神经网络的第一层假如他，它能够充当一种自适应的前处理，替代 Sci-Kit Learn 的 StandardScaler 之类的东西。

Binary Classification

Apply deep learning to another common task.

Introduction

课程到目前为止，我们已经学了神经网络如何解决线性问题。现在我们开始学习神经网络解决其他机器学习问题：分类。到目前为止我们学的大部分仍然适用。主要不同在于我们使用的损失函数以及最终层输出我们需要的结果。

Binary Classification

二分类是一个常见的机器学习问题。您可能想要预测客户是否有可能进行购买、信用卡交易是否存在欺诈、深空信号是否显示出新行星的证据等等，这些都是二分类问题。

在原始数据中，分类可能以字符串表现像“yes” and “No”；或者个“Dog” and “Cat”。在用数据之前需要将标签分类：一种分类方法是可以将标签一类设置为0，另一类设置为1。分配数字标签将数据编程可以在神经网络中使用的形式。

Accuracy and Cross-Entropy

准确性（accuracy）是用来判断分类问题成功与否的许多指标之一。准确性是正确预测在总预测中的占比：accuracy = number_correct/total。一个总是能准确预测的模型他的准确性值为1.0。其他相等的情况下，无论数据集中分类发生的频率是否相当，准确性都是一个合理的度量。

准确性的问题在于它不能被当作损失函数看待。SGD需要一个损失函数来平滑改变，但是准确性，做一个计算的比率，变化是“跳跃”的。所以，不得不选择一个可以代替损失函数的。这种代替是交叉熵函数（cross-entropy function）。

现在，回想一下损失函数在训练期间定义了网络的目标。在回归中，我们的目标是使预测结果和期望结果之间的差距越小越好。我们选择MAE来计算这种差距。

对于分类问题，我们想要的是概率之间的距离，这就是交叉熵可以提供的。交叉熵是一种对从一个概率分布到另一个概率分布的距离的度量。

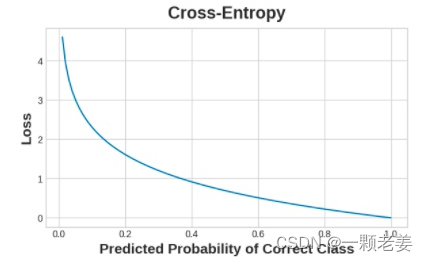
这个想法是我们希望我们的网络以 1.0 的概率预测正确的类别。预测概率离 1.0 越远，交叉熵损失就越大。

我们使用交叉熵的技术原因有点微妙，但本节的主要内容就是：使用交叉熵进行分类损失；您可能关心的其他指标（如准确性）会随之提高。

Making Probabilities with the Sigmoid Function

交叉熵和准确性都需要输入概率，也就是0-1之间的数组。为了使密集层输出的真实数据转变为概率，我们需要一种新的激活函数，为sigmoid activation。

为了获得最终的预测类别，我们定义了一个阈值概率。通常是 0.5，我们将概率低于 0.5 表示标签为 0 的类，概率值为0.5 或以上表示标签为 1 的类。 threshold=0.5是 Keras 默认使用的准确度指标([accuracy metric])。