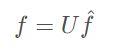最基础的GNN与GCN理解

一、为何引入GNN与GCN？

先回忆一下CNN：CNN常用于处理图像、语音——它们都是一种规则的、欧几里得结构的数据，同时拥有空间不变性（输入扭曲但输出仍不变）。CNN中的卷积是一种离散卷积（即加权求和），本质上就是利用一个共享参数的过滤器（kernel），通过计算中心像素点以及相邻像素点的加权和来构成feature map、实现空间特征的提取，其中的加权系数就是卷积核的权重系数(W)。

CNN中的卷积核的系数如何确定？——随机化初值，然后根据误差函数通过反向传播梯度下降进行迭代优化。经迭代优化后的卷积核才能实现特征提取的作用。对于卷积网络而言，引入可优化的卷积参数很重要。

如何处理 非欧式空间 的结构（典型：社交网络）？——引入了GNN与GCN网络：利用『边的信息』对『节点信息』进行『聚合』从而生成新的『节点表示』。

二、GNN（图域角度）

1、能干嘛？

输入各个节点本身的特征以及节点之间的关系图，输出在考虑了图结构后各节点的最终表达特征。这个最终特征可用于分类、回归、关联预测…

2、怎么做？

分三步走：聚合、更新、循环。以下图为例（每个节点旁边的数字为该节点的特征向量）：

（1） 聚合&更新：考虑当前节点本身的信息的同时，也要考虑当前节点的邻居节点的信息。以A节点为例，其邻居包括B、C、D，采用某种聚合方式将ABCD的信息融合起来。融合方法如下（a、b、c为超参数）：

得到的值用于更新A节点的值。遍历其他节点、操作相同。
（2）循环：当仅循环一次时，当前节点仅多聚合了自己邻居的信息；但循环到第二次时，将聚合邻居的邻居的信息。
仍以A节点为例，在第一次循环中A与E无聚合关系（AE非邻居）；但在第二次循环中，A与C聚合时，此时的C已在第一轮循环中聚合了E的信息（CE邻居），因此在第二轮循环中，A也会聚合一定的E的信息（即使A与E无直接联系）。易知，若循环足够多，则可处理到很大范围内的节点的信息。

GNN快速理解

三、GCN

较GNN而言主要是聚合操作不同。GCN提取图特征的过程有两种理解方式：空域与频域。

GCN论文

0、频域角度个人快速理解（谨慎参考）

图中彩色标注部分为强对应关系。

1、频域角度

（1）拉普拉斯矩阵

基于原始图，易构造其节点的度矩阵D、邻接矩阵A。根据这些信息可构造如下几种拉普拉斯矩阵L：

a. 最简单的构造公式 L=D-A：

b. 对称归一化的拉普拉斯矩阵构造公式：

其中具体的元素取值为：

此式中间最长的那行与 三、2 节中step4对应。

拉普拉斯矩阵的特征分解

我们构造出的拉普拉斯矩阵是半正定矩阵，拥有良好的性质：必能进行特征分解且特征向量两两 正交。特征分解后的形式为：

其中，U是L的特征向量，中间为特征值组成的对角矩阵。上式中U的逆可以换成U的转置。

（2） 传统傅里叶变换

拓展：从数学角度理解傅里叶变换为何能做到将原始信号转为若干正交信号的组合

傅里叶变换一个本质理解就是：把任意一个函数表示成了若干个正交函数（由sin,cos 构成）的线性组合。通过傅里叶变换还能实现图域与频域的转换。由其公式知：

上式中，f（t）为原始信号，第三项为关于时间t的函数，对其进行最右侧项所示的积分后，t被消掉了（对谁积分谁就消失），频率w变成了自变量。其中，

这一部分叫做 傅里叶变换的基，也是 拉普拉斯算子的特征函数，w就和特征值相关。

PS. 对图像（照片那种）进行傅里叶变换后，将得到其频谱图（在频域的表示），图像中心代表低频，通常用于描述图的形状等信息；图像边缘为高频，用于描绘纹理和边缘。频谱图中，越亮的部分代表取值越高。

（3）GCN中 拉普拉斯矩阵和傅里叶变换的关系

a. Graph的拉普拉斯矩阵 是 离散的 拉普拉斯算子
b. Graph的拉普拉斯矩阵的 特征向量U =拉普拉斯算子的 特征函数exp(-iwt)
c. 拉普拉斯算子的 特征函数 是 傅里叶变换的 基

因此，求Graph的傅里叶变换的基 = 求Graph的拉普拉斯矩阵的特征向量

要额外注意，Graph上的傅里叶变换与传统傅里叶变换不同：前者离散、后者连续。因此仿照（2）中 传统傅里叶定义公式（连续–积分），得到Graph上的 某个 特征值的傅里叶变换（离散–求和）：

推广到 所有 特征值：

即，f 在Graph上傅里叶变换的矩阵形式为：

逆变换：

对GCN而言，经傅里叶变换后，实现了： 图域卷积 == >频域相乘（这样做的好处包括可以减少计算量等）。那先对图和卷积核做傅立叶变换（得到其频域表示）后相乘，再傅立叶反变换回来，就得到了图域卷积。对应公式如下：

2、 空域角度

GCN空域角度快速理解

以下解释gcn核心公式（即，如何聚合）推导思路，前提：

step1.考虑邻居节点对当前节点的影响


改为矩阵形式：

step2.追加考虑节点本身（A变成A+I ）

step3.追加归一化
若无归一化操作，可能会导致离群较远或者度较小的节点在聚合后特征较小，离群较近或者度较大的节点在聚合后特征较大。故引入归一化消除这一影响。增设：



step4.对称归一化
引入此步骤是考虑到了相连的两节点，度的差距很大的情况，如下：

B是A的唯一，但A只是B的鱼塘里的其中一个——这种情况下，若仍按照step3的计算方式，则对于A节点而言，B的一大坨特征都会加到A的身上，进而导致原本AB差距很大，但在一轮循环后A的特征向B靠近了很多，A的特征失真了。因此对两节点的度做几何平均：


由上式知：假设A的度为1，B的度为10000。度的几何平均作分母后：对A（B）而言只有一小部分（1/100）的B（A）的特征被考虑了进来。
将上式化成论文里的样子：

这个公式中：

A波浪=A+I，I是单位矩阵
D波浪是A波浪的度矩阵
H是每一层的特征，对于输入层的话，H就是X
σ是非线性激活函数
W是可训练的参数矩阵

通过这个公式来进行层层传播，传播两到三层的效果就可以。两层GCN传递公式为：