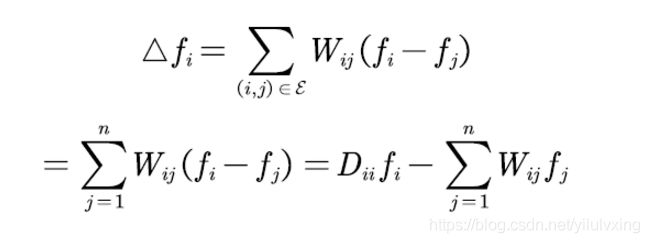图卷积神经网络1-谱域图卷积：拉普拉斯变换到谱域图卷积

知乎主页

备注：本篇博客摘自某培训机构上的图神经网络讲解的视频内容，该视频关于图神经网络入门讲解、经典算法的引入和优缺点的介绍比较详细，逻辑主线也比较清晰。因此记录分享下。

目录：

1. 图卷积近年发展
2. 图卷积简介
   2.1. 经典卷积神经网络的应用
   2.2. 经典卷积神经网络的局限
   2.3. 如何将卷积操作拓展到图结构数据中？
3. 谱域卷积
   3.1. 图谱卷积背景知识
   3.2. 图谱卷积的数学知识
   3.3. 图傅里叶变换
   3.4. 图傅里叶反变换
   3.5. 图傅里叶正变换
   3.6. 经典傅里叶变换与图傅里叶变换的对比
   3.7. 拉普拉斯特征向量和基本性质
4. 总结回顾

逻辑主线整理：

1. 由于经典卷积神经网络不能处理非结构化数据，因此考虑如何将卷积操作拓展到图结构数据中
2. 实现思路：
   1：谱域图卷积
   2：空域图卷积
3. 谱域卷积背景知识：
   1：卷积介绍：两信号在空域（或者时域）的卷积的傅立叶变换等于这两信号在频 域的傅立叶变换的乘积
   2：卷积意义：将空域信号转换到频域，然后相乘;将相乘的结果再转换到空域
   3：图上的傅立叶变换

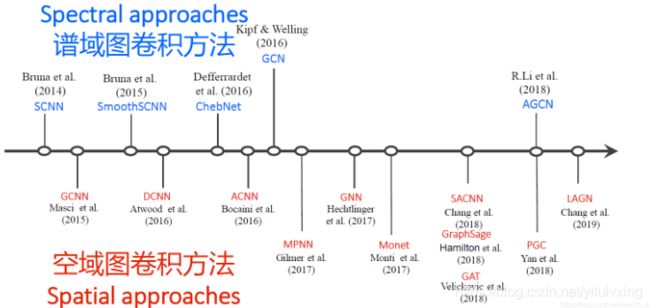
1：图卷积近年发展

图神经网络在在2016年以前相关文献较少，但是到2018年，图神经网络发展迅速。到2019年，图网络的文章数量大幅增加！
历年图论文的链接：https://github.com/naganandy/graph-based-deep-learning-literature/tree/master/conference-publications

2：图卷积简介

2.1：经典卷积神经网络的应用

经典卷积神经网络已经在多个领域取得了成功，主要包括：图片分类、计算机视觉、图片分割、目标检测等领域。

2.2：经典卷积神经网络的局限

经典卷积神经网络局限：只适合处理结构化数据，无法处理图结构数据

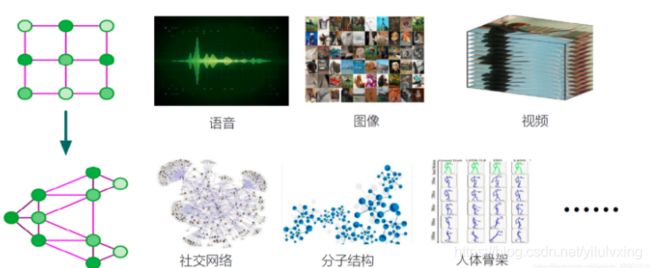
其中语音可以看作是一维向量，图像可以看作是二维矩阵，视频可以看作是三维矩阵。

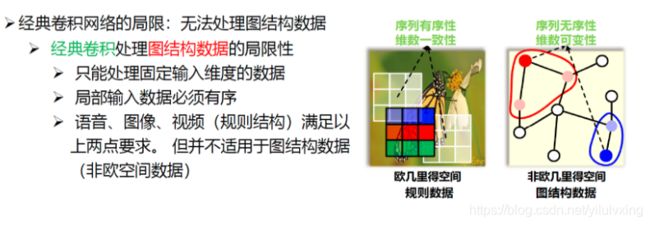
其中序列无序性是指：上图中红色节点的邻居节点有两个，而我们不知道它们谁应该排在前，谁应该排在后，这就是序列无序性。
维数可变性是指：上图中红色节点和蓝色节点的邻居节点个数是可以不相同的，这就是维数可变性。因此我们无法将3x3的卷积核应用到图数据上，这就是图卷积网络需要解决的问题。

2.3：如何将卷积操作拓展到图结构数据中？

实现思路1：谱域图卷积
谱域图卷积：

• 根据图谱理论和卷积定了，将数据由空域转换到谱域做处理
• 有较为坚实的理论基础

谱域图卷积也是本章重点

---

实现思路2：空域图卷积
空域图卷积：

• 不依靠图谱卷积理论，直接在空间上定义卷积操作
• 定义直观，灵活性强

---

图卷积经典模型回顾

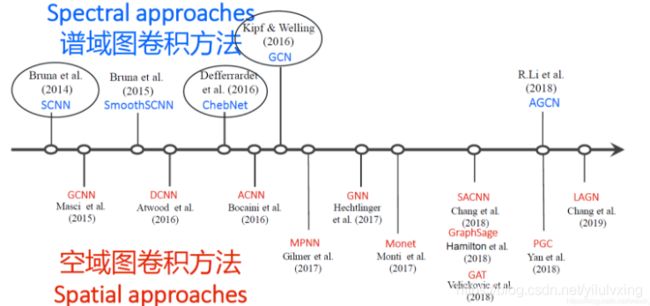
本章重点介绍谱域图卷积方法，主要由上图圈出来的三篇文章讲解，即SCNN、GCN和ChebNet三个模型。

3：谱域卷积

3.1：图谱卷积背景知识

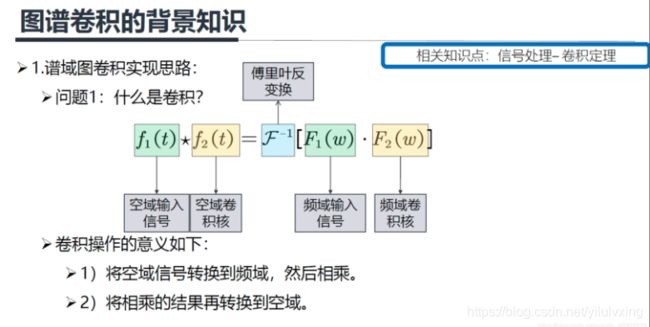
我们将 $f_1(t)$ 定义为空域输入信号, $f_2(t)$ 定义为空域卷积核，那么卷积核就可以这样定义： 首先将空域上的信号 $f_1(t)$ 转换到频域信号 $F_1(w),$ 然后相乘, 再将相乘后的结果通过傅里叶反变换 后再返回空域上去, 这个就是谱域图卷积的实现思路（将空域转换到频域上处理, 处理完再返 回)

前面所说的经典的卷积操作具有序列有序性和维数不变性的限制，使得经典卷积难以处理图数据, 也就是说对于一个3x3的卷积核，它的形状是固定的，它的感受野的中心节点必须要有八个领域才能使用卷积核，但是图上的节点的领域节点是不确定的，此外图上节点的领域节点也是没有顺序的，这就导致不能直接在空域使用经典的卷积。但是把数据从空域转换到频域，在频域处理数据时，只需要将每个频域的分量放大或者缩小就可以了，不需要考虑信号在空域上存在的问题, 这个就是谱域图卷积的巧妙之处。

如何定义图上的傅里叶变换？：

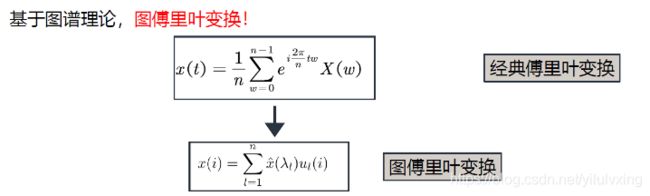
接下来部分介绍谱域图卷积的数学背景知识，包括傅里叶变换。

---

3.2：图谱卷积的数学知识

其中 $V$代表所有节点的集合（共n个）， $E$代表所有边的集合， $W$代表邻接矩阵（n x n的方阵）， $D$为度矩阵，定义为从 $i$节点出发的所有边的权重之和（n x n的方阵，是对角矩阵）。下面看一个例子中，权重都为1。


上面是拉普拉斯矩阵半正定的展开证明，涉及到矩阵知识点，感兴趣的可以看看，个人觉得记住结论即可。

---

拉普拉斯矩阵的相关性质：

---

拉普拉斯矩阵的谱分解：


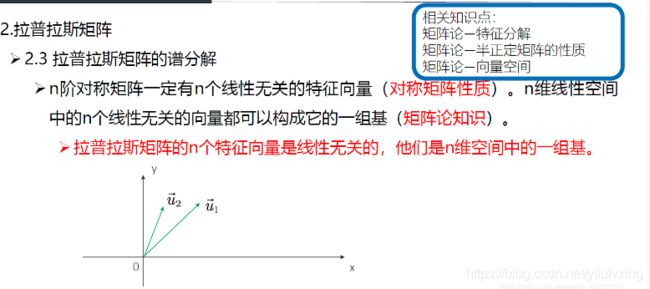
比如，在二维空间中有 $u_1$, $u_2$ 两个线性无关的向量，则它们可以表示这个二维空间中的所有向量，它们就是二维空间中的一组基。

上面就是在说拉普拉斯矩阵特征分解后的特征向量不但是n维空间中的一组基，而且还是正交的（相乘为0），简称标准正交基。

但是为什么拉普拉斯矩阵是度矩阵减邻接矩阵，也就是 $L=D-W$呢？原因是拉普拉斯矩阵是图上的一种拉普拉斯算子，接着看看拉普拉斯算子讲解与图上的拉普拉斯算子的证明（个人觉得也只需记住结论即可）：



上面右图就是两个变量的离散拉普拉斯矩阵算子的解释，也就是说对于某个中心像素（红色）的算子为周围四个像素之和减去4倍的自己。

---

拉普拉斯矩阵与拉普拉斯算子：

对上面公式就是做一下简单的变换，只要是理解了前面讲的几个矩阵的定义，就很好理解了，对于n个节点则由变换后的公式得出（上面右边公式）：

---

结论：

---

拉普拉斯矩阵性质总结：

以上就是拉普拉斯矩阵的性质，正是因为有了这些性质，才会使用拉普拉斯矩阵来图方面的工作。

---

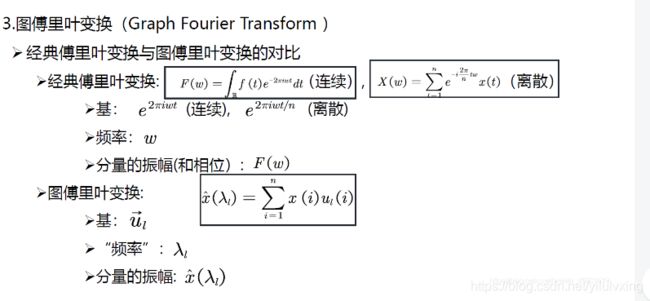
3.3：图傅里叶变换

上图中蓝色线段代表信号的大小，类似于图像上灰度图像像素，像素越高，画的这个线段越长。图 上的信号也是类似的，只不过若一个信号有c个通道, 那么 $x=\left[x_1,x_2,\dots ,x_n\right]\in R^{n\ast c},$ 彩色图像 有R,G,B三个通道, 则 $c=3$ 。下面为了讲解简单, 先假设图上的一个信号只有一个通道，多个通道原理也是类似的。

---

傅里叶变换的物理意义：

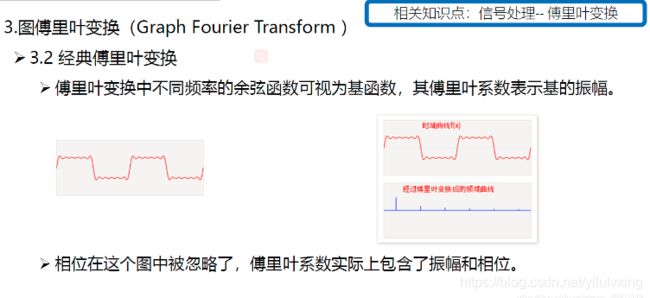
下面这个图就是上面左图：

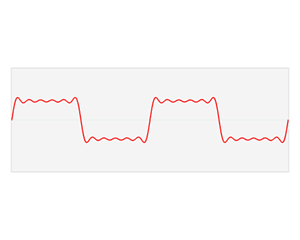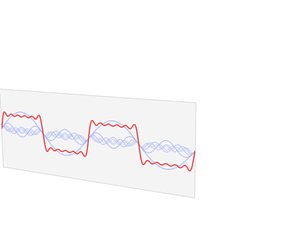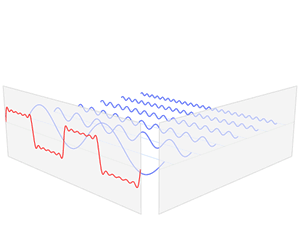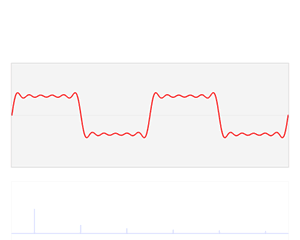
有篇关于傅里叶变换的直观解释，傅里叶变换的解释链接，经典傅里叶变换其实是说：一个信号由不同频率的基函数信号叠加而成，比如上图中红色信号是原信号，蓝色信号是不同频率上的基函数信号（余弦或者正弦函数）。上面右图中，红色原信号可以由不同频率的基函数线性组合而成，蓝色的高度表示基前面的系数，也就是所谓的傅里叶系数，也就是
原函数在这个基上的坐标分量。

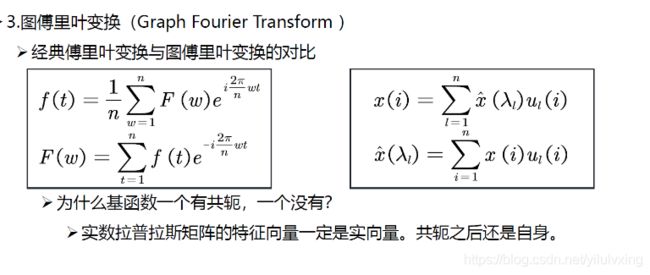
上面的公式是离散的傅里叶变换，它和图傅里叶变换比较接近（图傅里叶变换也是离散的）， $F(w)$ 就是上面所说的蓝线的高低。

上图中，左边公式是连续傅里叶变换，右边是离散傅里叶变换。

---

上面公式的 $x$ 就是输入信号, $\hat{x}\left({\lambda }_1\right)$ 就是前面提到的傅里叶系数。

---

3.4：图傅里叶反变换

上面公式中，右边的 $U\hat{x}$的 $\hat{x}$就是谱域上的信号。

3.5：图傅里叶正变换

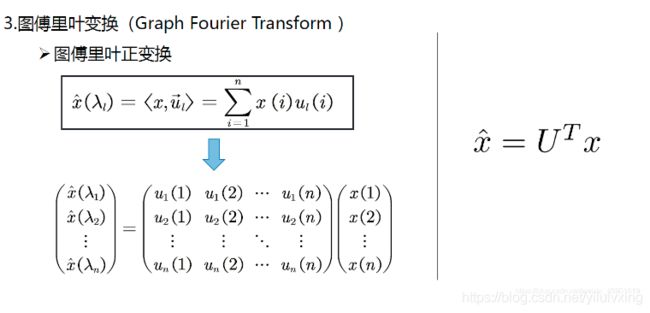
傅里叶正变换就是求傅里叶反变换前面的系数，也就是每个基函数前面的振幅，具体做法看前面定义，也就是做输入信号$x$ 和基函数 $u$的内积。

---

3.6：经典傅里叶变换与图傅里叶变换的对比

3.7：拉普拉斯特征向量和基本性质

本征函数和本征向量可以认为是特征值和特征向量的扩展。特征向量是针对矩阵而言，而本征向量是针对算子而言的，很接近，如果宽泛一点，可以认为是一个概念。


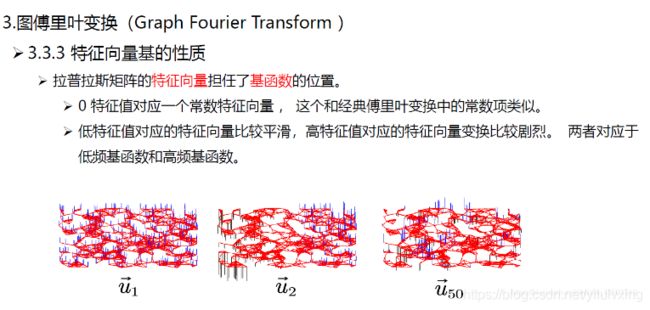
上图是三个不同的特征值对应的特征向量的示例，$u_1$是最小的特征值对应的特征向量（可以看出很平滑），$u_2$是第二小的特征值对应的特征向量（不太平滑），$u_{5}0$是第五十小的特征值对应的特征向量（很不平滑）。

Zero crossing是指有边相邻的两个节点上对应的值一个大于0，一个小于0，每出现这样的一条边，Zero crossing就加一，通过Zero crossing的个数可以粗略的判断信号的震荡程度，或者可以说是平滑程度。从右图可以看到，大特征值可以视为高频信号，小特征值可以视为低频信号。

---

特征向量基的基本性质：

---

4：总结回顾

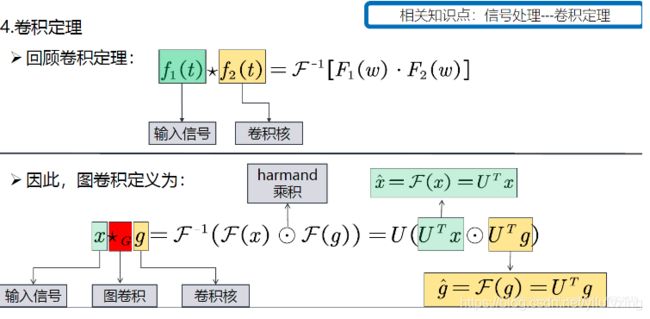
图上的卷积定义：先对 $F(x)$ 和 $F(g)$ 做傅里叶正变换，然后在谱域上做 harmand 乘积, 也就是 $F(x)\odot F(g)$
最后通过傅里叶反变换 $F^{-1}$ 将结果返回到空域。前面讲了傅里叶正变换就是 $\hat{x}=U^{T}x,$ 则傅里叶反变换就是 $U\left(U^{T}x\odot U^{T}g\right)$ 。

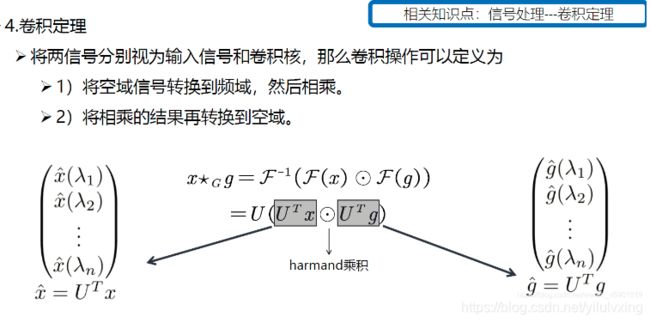
为了更加清晰理解上述公式，重新整理并推导：
$x{\star }_G{g}_{\theta }=U{g}_{\theta }{U}^{T}x=U\left(U^{T}x\right)\odot \left(U^{T}g\right)$
$=U\left(\begin{array}{c}\hat{x}\left({\lambda }_1\right)\\ \hat{x}\left({\lambda }_2\right)\\ ⋮\\ \hat{x}\left({\lambda }_n\right)\end{array}\right)\odot \left(\begin{array}{c}\hat{g}\left({\lambda }_1\right)\\ \hat{g}\left({\lambda }_2\right)\\ ⋮\\ \hat{g}\left({\lambda }_n\right)\end{array}\right)$
=$U\left(\begin{array}{c}\hat{g}\left({\lambda }_1\right)\hat{x}\left({\lambda }_1\right)\\ \hat{g}\left({\lambda }_2\right)\hat{x}\left({\lambda }_2\right)\\ ⋮\\ \hat{g}\left({\lambda }_n\right)\hat{x}\left({\lambda }_n\right)\end{array}\right)$
$=U\left(\begin{array}{ccc}\hat{g}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{g}\left({\lambda }_n\right)\end{array}\right)\left(\begin{array}{c}\hat{x}\left({\lambda }_1\right)\\ \hat{x}\left({\lambda }_2\right)\\ ⋮\\ \hat{x}\left({\lambda }_n\right)\end{array}\right)$
$=U\left(\begin{array}{ccc}\hat{g}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{g}\left({\lambda }_n\right)\end{array}\right)U^{T}x$
上面就是谱域图卷积最终的公式，所有的谱域图卷积的原理就是这个公式，只是对滤波器 $\hat{g}$做了不同的处理。这个公式的意义是：卷积核信号（或者说滤波器信号）$\hat{g}$是一个n维的向量，它的作用是将原信号的不同的分量进行一个放大或者缩小，这取决于卷积核信号在谱域上不同元素的值。

下一篇：
图卷积神经网络2-谱域卷积：SCNN/ChebNet/GCN的引入和介绍

图卷积神经网络3-空域卷积：GNN/GraphSAGE/PGC的引入和介绍

图卷积神经网络4-空域卷积：空域卷积局限性分析和过平滑解决方案

图卷积神经网络5：图卷积的应用

知乎主页