【图机器学习】图神经网络入门（二）图上的傅里叶变换

1 前言

  内容为自己的学习总结，其中多有借鉴他人的地方，最后一并给出链接。
  在之前的文章中已经简单介绍了谱图理论【图机器学习】图神经网络入门（一）谱图理论，在本小节主要介绍如何从传统的傅里叶变换到图上的傅里叶变换。其中个人理解有错的地方希望，大家多多指正。
  这里在此重申一下为什么学习图傅里叶变换，对于图来说，直接进行卷积是困难的，因为图不具备图像那样规则的网格结构，因此考虑应用图傅里叶变换将网络的空域信息映射到频域来应用卷积定理完成卷积操作。

2 传统的傅里叶变换

  傅里叶公式的推导建议读参考文献【1】【2】，参考文献写的比较详细。在不想看公式的情况下理解傅里叶变换可以看参考文献【3】，在有一定傅里叶理论基础但是模糊想继续了解一些模糊的问题如：（1）周期信号傅里叶级数表示什么内容？（2）信号的频谱表示什么？（3）通过信号的频谱我们能知道什么？（4）信号的时域和频域的关系是什么？可以看参考文献【4】。

  这里主要列出几个重要的结论和概念。

在经典傅里叶变换中，让我们来看一下本质何在:

• 傅里叶正变换的本质是：求线性组合的系数。也就是由原函数和基函数的共轭的内积求得。
  $$F(\omega )=\mathcal{F}[f(t)]=\int f(t)e^{-i\omega t}dt$$
• 傅里叶反变换的本质是：把任意一个函数表示成了若干个正交基函数的线性组合。
  $${\mathcal{F}}^{-1}[F(\omega )]=\frac{1}{2\Pi }\int F(\omega )e^{i\omega t}d\omega$$

  傅里叶变换是将函数$f(x)$拆解成无数个不同频率正弦波之和的过程，$F(w)$表示角频率为$w$的波的系数。傅里叶变换也可以看做函数$f(t)$向基函数$e^{-iwt}$投影（而这个基$e^{-iwt}$恰好是拉普拉斯算子的特征向量，这个很重要，$w$就表示对应基上的坐标。

  可以结合参考文献【3】理解，为什么傅里叶变换可以看做函数$f(t)$向基函数$e^{-iwt}$的投影。

  解释一下函数的投影，先用向量投影做一个类比。比如一个二维空间中的向量$a=[1,2]$
想要得到在一组基（基之间相互正交且模长为1）下的坐标表示，只需要向量$a$与基做内积运算即可。函数$f(t)$可以想象成一个长度为无穷的向量，函数空间中的内积定义为积分。上面傅里叶变换的公式中，将$e^{-iwt}$看做基，则整个式子就是在算$f(t)$在$e^{-iwt}$这个基上的坐标，所有的$w$都算一次，就可以得到$f(t)$在$e^{-iwt}$, $w\in (-\infty ,\infty )$这组基上的完整坐标，这就是$F(w)$这个函数的含义。参考文献【5】

3 图傅里叶变换

  之前已经介绍了拉普拉斯算子与拉普拉斯矩阵的关系，可以得出结论拉普拉斯矩阵是图上的一种拉普拉斯算子。
  将拉普拉斯算子作用于$e^{-iwt}$，可得：
$$\Delta e^{-i\omega t}=\frac{{\partial }^2}{\partial t^2}{e}^{-i\omega t}=-{\omega }^2{e}^{-i\omega t}$$

  从数学上看$e^{-iwt}$是拉普拉斯算子的特征函数（满足特征方程）, $w$就和特征值有关。根据广义特征方程$A\mathbf{x}=\lambda \mathbf{x}$，$e^{-iwt}$就是拉普拉斯算子的特征向量。

  在这里就可以类比传统的傅里叶变换（参考文献【5】【6】【7】【8】），在传统傅里叶变换中使用$e^{-iwt}$作为基，而$e^{-iwt}$是拉普拉斯的特征向量，又因为拉普拉斯矩阵是图上的拉普拉斯算子，所以图上的傅里叶变换所以可以用拉普拉斯矩阵的特征向量作为图傅里叶投影的基。（这个不算严谨，但是可以类比理解）。

  
  总而言之,图傅里叶变换是使用类比的方式直接定义的，并非经过严格推导，类比的方法如下：
  ①拉普拉斯算子与拉普拉斯矩阵：拉普拉斯算子的作用是能够得到一个点在某些自由度上微扰以后获得的增益，而拉普拉斯矩阵能够获得网络中的每个节点微扰以后从它的邻居节点上获得的增益，也就是说：拉普拉斯矩阵之于网络就相当于拉普拉斯算子之于函数。

  ②拉普拉斯算子的特征函数与拉普拉斯矩阵的特征向量：傅里叶变换的基函数$e^{-iwt}$是拉普拉斯算子的特征函数，那么同样的图傅里叶变换的基向量就是拉普拉斯矩阵的特征向量$u_k$。

  ③拉普拉斯算子的特征值与拉普拉斯矩阵的特征值：傅里叶变换的频率$w$是拉普拉斯算子的特征值，那么同样的图傅里叶变换的频率就是拉普拉斯矩阵的特征值${\lambda }_k$。（参考文献【9】，强烈推荐）
$$\begin{array}{l}{\nabla }^2{e}^{-i\omega t}=-{\omega }^2{e}^{-i\omega t}\\ \Uparrow \\ L{\mu }_k={\lambda }_k{\mu }_k\end{array}$$

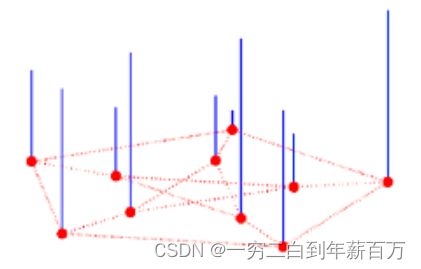
  再回顾一下经典傅里叶变换的本质：一个信号由不同频率的基函数信号叠加而成，比如下图中红色信号是原信号，蓝色信号是不同频率上的基函数信号（余弦或者正弦函数）。下面右图中，红色原信号可以由不同频率的基函数线性组合而成，蓝色的高度表示基前面的系数，也就是所谓的傅里叶系数，也就是原函数在这个基上的坐标分量。

  由上可知，既然对于函数来说拉普拉斯算子的特征值和特征函数能够用于函数的傅里叶变换，那么对于图来说拉普拉斯矩阵的特征值和特征向量就能够用于图的傅里叶变换。换句话说，傅里叶变换是以拉普拉斯算子的特征函数为基进行投影，那么图傅里叶变换就以拉普拉斯矩阵的特征向量为基进行投影，因此图傅里叶变换定义为：
$$F\left({\lambda }_k\right)=\sum _{i=1}^{N}f(i){\mu }_k(i)$$
  图上的信号一般表示为一个向量，假设有$n$个节点，则图上的信号记为：
$$f=[f_1,f_2,f_3,......f_n{]}^T\in R^{n\times c}$$
$c$ 理解为特征的通道数或者节点特征的维度。

• $f$是图上的$n$维向量，可以表示某个点的特征向量，$f(i)$表示第$i$个特征
• $u_k(i)$表示第$k$个特征向量的第$i$个分量
• $f$的图傅里叶变换就是与${\lambda }_k$对应的特征向量$u_k$进行内积运算
• ${\lambda }_k$就对应于频率 $\omega$
• $\hat{f}$ 表示$f$的傅里叶变换

  上式中，$f$还是表示由图节点信息构成的向量，${\lambda }_k$和${\mu }_k$分别表示拉普拉斯矩阵的特征值和特征向量。现在用$\hat{f}$表示$f$经过傅里叶变换之后的坐标，那么图傅里叶变换可以表示成矩阵形式：
$$\hat{f}=\left(\begin{array}{c}{\hat{f}}_1\\ ⋮\\ {\hat{f}}_N\end{array}\right)=\left(\begin{array}{ccc}{\mu }_1(1)& \cdots & {\mu }_1(N)\\ ⋮& \ddots & ⋮\\ {\mu }_N(1)& \cdots & {\mu }_N(N)\end{array}\right)\left(\begin{array}{c}{f}_1\\ ⋮\\ f_N\end{array}\right)=U^{T}f$$
从矩阵乘法理解可以理解为，图上的所有特征 $f$ 在特征值${\lambda }_k$对应的特征向量${\mu }_k$的投影的分量加和得到了${\hat{f}}_{1,2,3}$
  同样也可以得到图傅里叶变换的逆变换:傅里叶逆变换的本质是把任意一个函数表示成若干个正交基函数的线性组合。因此：
$$\begin{array}{l}f=\hat{f}\left({\lambda }_1\right)u_1+\hat{f}\left({\lambda }_2\right)u_2+\cdots +\hat{f}\left({\lambda }_k\right)u_n\\ f(i)={\sum }_{l=1}^n\hat{f}\left({\lambda }_k\right)u_n(i)\end{array}$$
矩阵形式为：
$$f=\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(n)\end{array}\right)=\left(\begin{array}{cccc}{\mu }_1(1)& {\mu }_2(1)& \cdots & {\mu }_n(1)\\ {\mu }_1(2)& {\mu }_2(2)& \cdots & {\mu }_n(2)\\ ⋮& ⋮& \ddots & ⋮\\ {\mu }_1(n)& {\mu }_2(n)& \cdots & {\mu }_n(n)\end{array}\right)\left(\begin{array}{c}\hat{f}\left({\lambda }_1\right)\\ \hat{f}\left({\lambda }_2\right)\\ ⋮\\ \hat{f}\left({\lambda }_k\right)\end{array}\right)=U\hat{f}$$
$$f=U{U}^{-1}f=U{U}^{T}f=U\hat{f}$$
参考文献【7】【9】。
  这里再做一下小结：傅里叶正变换就是求傅里叶反变换前面的系数，也就是每个基函数前面的振幅，具体做法看前面定义，也就是做输入信号$f$ 和基函数$u$的内积。傅里叶反变换就是把$f$图中的信号函数，表示成若干个正交基函数的线性组合。

4 总结

  根据图傅里叶变换，可以将定义在图上节点的信号$f\in R^n$，从空间域转到谱域

• 空间域——>谱域  $\hat{f}=U^{T}f$
• 谱域——>空间域  $f=U\hat{f}$

5 参考文献

[1]傅里叶级数与傅里叶变换（一）
[2]傅里叶级数与傅里叶变换（二）
[3]万物皆可傅里叶|傅里叶分析之掐死教程（完整版
[4]信号傅里叶变换系列文章（1）：傅里叶级数、傅里叶系数以及傅里叶变换
[5]图傅里叶变换
[6]如何理解 Graph Convolutional Network（GCN）？
[7]图卷积神经网络1-谱域图卷积：拉普拉斯变换到谱域图卷积
[8]GNN 教程：漫谈谱图理论和GCN的起源
[9]图神经网络中的谱图理论基础
[10]从传统傅里叶变换到图卷积
[11]图卷积神经网络(GCN)详解:包括了数学基础(傅里叶，拉普拉斯)
[12]Alejandro RIbeiro-GNN笔记1-3——图信号处理
[13]图神经网络基础二：谱图理论 _
[14]图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导