GAT 算法原理介绍与源码分析
GAT 算法原理介绍与源码分析
文章目录
- GAT 算法原理介绍与源码分析
-
- 零. 前言 (与正文无关, 请忽略)
-
- 广而告之
- 一. 文章信息
- 二. 核心观点
- 三. 核心观点解读
- 四. 源码分析
-
- 4.1 Graph Attention Layer
- 4.2 GAT 网络
- 五. 总结
零. 前言 (与正文无关, 请忽略)
对自己之前分析过的文章做一个简单的总结:
- 机器学习基础: LR / LibFM
- 特征交叉: DCN / PNN / DeepMCP / xDeepFM / FiBiNet / AFM
- 用户行为建模: DSIN / DMR / DMIN
- 多任务建模: MMOE
- Graph 建模: GraphSage
广而告之
可以在微信中搜索 “珍妮的算法之路” 或者 “world4458” 关注我的微信公众号;另外可以看看知乎专栏 PoorMemory-机器学习, 以后文章也会发在知乎专栏中. CSDN 上的阅读体验会更好一些, 地址是: https://blog.csdn.net/eric_1993/category_9900024.html
一. 文章信息
- 论文标题: Graph Attention Networks
- 论文地址: https://arxiv.org/pdf/1710.10903.pdf
- 代码地址: https://github.com/PetarV-/GAT
- 发表时间: ICLR 2018
- 论文作者: 详见文章
- 作者单位: University of Cambridge
二. 核心观点
GAT (Graph Attention Networks) 采用 Attention 机制来学习邻居节点的权重, 通过对邻居节点的加权求和来获得节点本身的表达.
三. 核心观点解读
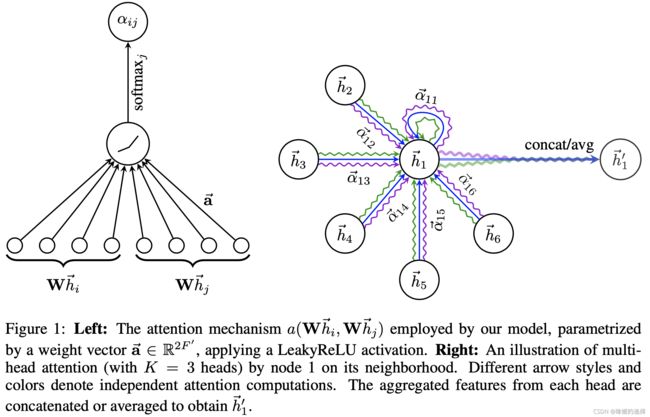
GAT 的实现机制如下图所示:
注意右图中, GAT 采用 Multi-Head Attention, 图中有 3 种颜色的曲线, 表示 3 个不同的 Head. 在不同的 Head 下, 节点 h ⃗ 1 \vec{h}_{1} h1 可以学习到不同的 embedding, 然后将这些 embedding 进行 concat/avg 便生成 h ⃗ 1 ′ \vec{h}_{1}^{\prime} h1′.
下面直接看分析代码吧.
四. 源码分析
GAT 的源码位于: https://github.com/PetarV-/GAT
GAT 网络本身是通过堆叠多个 Graph Attention Layer 层构成的, 首先介绍 Graph Attention Layer 的实现.
4.1 Graph Attention Layer
Graph Attention Layer 的定义:
设 N N N 个输入节点的特征为: h = { h ⃗ 1 , h ⃗ 2 , … , h ⃗ N } , h ⃗ i ∈ R F \mathbf{h}=\left\{\vec{h}_{1}, \vec{h}_{2}, \ldots, \vec{h}_{N}\right\}, \vec{h}_{i} \in \mathbb{R}^{F} h={h1,h2,…,hN},hi∈RF, 采用 Attention 机制生成新的节点特征 h ′ = { h ⃗ 1 ′ , h ⃗ 2 ′ , … , h ⃗ N ′ } , h ⃗ i ′ ∈ R F ′ \mathbf{h}^{\prime}=\left\{\vec{h}_{1}^{\prime}, \vec{h}_{2}^{\prime}, \ldots, \vec{h}_{N}^{\prime}\right\}, \vec{h}_{i}^{\prime} \in \mathbb{R}^{F^{\prime}} h′={h1′,h2′,…,hN′},hi′∈RF′ 作为输出.
Attention 系数按如下方式生成:
α i j = exp ( LeakyReLU ( a → T [ W h ⃗ i ∥ W h ⃗ j ] ) ) ∑ k ∈ N i exp ( LeakyReLU ( a → T [ W h ⃗ i ∥ W h ⃗ k ] ) ) \alpha_{i j}=\frac{\exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{k}\right]\right)\right)} αij=∑k∈Niexp(LeakyReLU(aT[Whi∥Whk]))exp(LeakyReLU(aT[Whi∥Whj]))
其中 a → ∈ R 2 F ′ \overrightarrow{\mathbf{a}} \in \mathbb{R}^{2 F^{\prime}} a∈R2F′, 而 ∥ \| ∥ 表示 concatenation 操作.
其代码实现位于: https://github.com/PetarV-/GAT/blob/master/utils/layers.py. 注意在代码实现中, 作者的写法很简洁精妙, 不是照着上面的公式直接写的, 而是做了一点程度的变换.
由于 a → ∈ R 2 F ′ \overrightarrow{\mathbf{a}} \in \mathbb{R}^{2 F^{\prime}} a∈R2F′, 因此令 a → = [ a → 1 , a → 2 ] \overrightarrow{\mathbf{a}} = [ \overrightarrow{\mathbf{a}}_{1}, \overrightarrow{\mathbf{a}}_{2}] a=[a1,a2], 其中 a → 1 ∈ R F ′ , a → 2 ∈ R F ′ \overrightarrow{\mathbf{a}}_{1}\in\mathbb{R}^{F^{\prime}}, \overrightarrow{\mathbf{a}}_{2}\in\mathbb{R}^{F^{\prime}} a1∈RF′,a2∈RF′, 那么 a → T [ W h ⃗ i ∥ W h ⃗ j ] \overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right] aT[Whi∥Whj] 其实等效于 a → 1 T W h ⃗ i + a → 2 T W h ⃗ j \overrightarrow{\mathbf{a}}_{1}^T\mathbf{W}\vec{h}_{i} + \overrightarrow{\mathbf{a}}_{2}^T\mathbf{W}\vec{h}_{j} a1TWhi+a2TWhj, 下面代码实现中, 采用的就是等效的写法.
def attn_head(seq, out_sz, bias_mat, activation, in_drop=0.0, coef_drop=0.0, residual=False):
"""
参数介绍:
+ seq: 输入节点特征, 大小为 [B, N, E], 其中 N 表示节点个数, E 表示输入特征的大小
+ out_sz: 输出节点的特征大小, 我这里假设为 H
+ bias_mat: 做 Attention 时一般需要 mask, 比如只对邻居节点做 Attention 而不包括 Graph 中其他节点.
它的大小为 [B, N, N], bias_mat 的生成方式将在下面介绍
+ 其余参数略.
attn_head 输入大小为 [B, N, E], 输出大小为 [B, N, out_sz]
"""
with tf.name_scope('my_attn'):
if in_drop != 0.0:
seq = tf.nn.dropout(seq, 1.0 - in_drop)
## conv1d 的参数含义依次为: inputs, filters, kernel_size
## seq: 大小为 [B, N, E], 经过 conv1d 的处理后, 将得到
## 大小为 [B, N, H] 的输出 seq_fts (H 表示 out_sz)
## 这一步就是公式中对输入特征做线性变化 (W x h)
## seq_fts 就是节点经映射后的输出特征
seq_fts = tf.layers.conv1d(seq, out_sz, 1, use_bias=False)
## f_1 和 f_2 就是我在上面介绍过的, 将向量 a 拆成 a1 和 a2, 然后分别和输入特征进行内积
## 再利用 f_1 + tf.transpose(f_2, [0, 2, 1])
## 得到每个节点相对其他节点的权重, logits 的大小为 [B, N, N]
f_1 = tf.layers.conv1d(seq_fts, 1, 1) ## [B, N, 1]
f_2 = tf.layers.conv1d(seq_fts, 1, 1) ## [B, N, 1]
logits = f_1 + tf.transpose(f_2, [0, 2, 1]) ## [B, N, N]
## 将 logits 经过 softmax 前, 还需要加上 bias_mat, 大小为 [B, N, N], 可以认为它就是个 mask,
## 对于每个节点, 它邻居节点在 bias_mat 中的值为 0, 而非邻居节点在 bias_mat 中的值为一个很大的负数,
## 代码中设置为 -1e9, 这样在求 softmax 时, 非邻居节点对应的权重值就会近似于 0
coefs = tf.nn.softmax(tf.nn.leaky_relu(logits) + bias_mat)
if coef_drop != 0.0:
coefs = tf.nn.dropout(coefs, 1.0 - coef_drop)
if in_drop != 0.0:
seq_fts = tf.nn.dropout(seq_fts, 1.0 - in_drop)
## coefs 大小为 [B, N, N], 表示每个节点相对于它邻居节点的 Attention 系数,
## seq_fts 大小为 [B, N, H], 表示每个节点经变换后的特征
## 最后得到 ret 大小为 [B, N, H]
vals = tf.matmul(coefs, seq_fts)
ret = tf.contrib.layers.bias_add(vals)
# residual connection
if residual:
if seq.shape[-1] != ret.shape[-1]:
ret = ret + conv1d(seq, ret.shape[-1], 1)
else:
ret = ret + seq
return activation(ret) # activation
这里再补充两个小要点: conv1d 的实现以及 bias_mat 的生成. 首先看 conv1d 的实现:
再来看 bias_mat 的生成, 代码位于: https://github.com/PetarV-/GAT/blob/master/utils/process.py, 实现如下:
def adj_to_bias(adj, sizes, nhood=1):
"""
输入参数介绍:
+ adj: 大小为 [B, N, N] 的邻接矩阵
+ sizes: 节点个数, [N]
+ nhood: 设置多跳, 如果 nhood=1, 则只考虑节点的直接邻居; nhood=2 则把二跳邻居也考虑进去
"""
nb_graphs = adj.shape[0]
mt = np.empty(adj.shape)
for g in range(nb_graphs):
mt[g] = np.eye(adj.shape[1])
## 考虑多跳邻居的关系, 比如 nhood=2, 则把二跳邻居的关系考虑进去, 之后在 Graph Attention Layer 中,
## 计算权重系数时, 也会让二跳邻居参与计算.
for _ in range(nhood):
mt[g] = np.matmul(mt[g], (adj[g] + np.eye(adj.shape[1])))
## 如果两个节点有链接, 那么设置相应位置的值为 1
for i in range(sizes[g]):
for j in range(sizes[g]):
if mt[g][i][j] > 0.0:
mt[g][i][j] = 1.0
## 最后返回上面 attn_head 函数中用到的 bias_mat 矩阵,
## 对于没有链接的节点位置, 设置一个较大的负数 -1e9; 而有链接的位置, 元素为 0
## 这样相当于 mask, 用于 Attention 系数的计算
return -1e9 * (1.0 - mt)
4.2 GAT 网络
代码定义于: https://github.com/PetarV-/GAT/blob/master/models/gat.py, 实现如下:
class GAT(BaseGAttN):
def inference(inputs, nb_classes, nb_nodes, training, attn_drop, ffd_drop,
bias_mat, hid_units, n_heads, activation=tf.nn.elu, residual=False):
"""
inputs: 大小为 [B, N, E]
n_heads: 输入为 [8, 1], n_heads[0]=8 表示使用 8 个 Head 处理输出特征, n_heads[-1]=1, 使用 1 个 Head 处理输出特征
"""
attns = []
for _ in range(n_heads[0]):
## attn_head 的输出大小为 [B, N, H]
attns.append(layers.attn_head(inputs, bias_mat=bias_mat,
out_sz=hid_units[0], activation=activation,
in_drop=ffd_drop, coef_drop=attn_drop, residual=False))
h_1 = tf.concat(attns, axis=-1)
## 重复以上过程
for i in range(1, len(hid_units)):
h_old = h_1
attns = []
for _ in range(n_heads[i]):
attns.append(layers.attn_head(h_1, bias_mat=bias_mat,
out_sz=hid_units[i], activation=activation,
in_drop=ffd_drop, coef_drop=attn_drop, residual=residual))
h_1 = tf.concat(attns, axis=-1)
## 得到输出
out = []
for i in range(n_heads[-1]):
out.append(layers.attn_head(h_1, bias_mat=bias_mat,
out_sz=nb_classes, activation=lambda x: x,
in_drop=ffd_drop, coef_drop=attn_drop, residual=False))
logits = tf.add_n(out) / n_heads[-1]
return logits
主要内容为堆叠 Graph Attention Layer, 就不详细介绍了.
五. 总结
没有总结, 内心只有纠结.