深度学习（四十）——深度强化学习（3）Deep Q-learning Network（2）, DQN进化史

Deep Q-learning Network（续）

Nature DQN

DQN最早发表于NIPS 2013，该版本的DQN，也被称为NIPS DQN。NIPS DQN除了提出DQN的基本概念之外，还使用了《机器学习（三十三）》中提到的Experience Replay技术。

2015年初，Deepmind在Nature上提出了改进版本，是为Nature DQN。它改进了Loss函数：

$$L=(r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },w^{-})-Q(s,a,w){)}^2$$

上式中，计算目标Q值的网络使用的参数是$w^{-}$，而不是w。也就是说，原来NIPS DQN的target Q网络是动态变化的，跟着Q网络的更新而变化，这样不利于计算目标Q值，导致目标Q值和当前的Q值相关性较大。

因此，Deepmind提出可以单独使用一个目标Q网络。那么目标Q网络的参数如何来呢？还是从Q网络中来，只不过是延迟更新。也就是每次等训练了一段时间再将当前Q网络的参数值复制给目标Q网络。

个人理解这里的机制类似于进化算法。变异既可以是进化，也可以是退化，只有进化的Q网络才值得保留下来。

这在下文介绍的Leela Zero项目的训练过程中体现的很明显：一开始我们只训练一个简单的AI，然后逐渐加深加大网络，淘汰废物AI，得到更优秀的AI。

为了使进化生效，在一段时间内保持目标Q网络不变就是很显然的了——你过不了我这关，就没资格继续下去了。

参考

https://zhuanlan.zhihu.com/p/21262246

DQN从入门到放弃1 DQN与增强学习

https://zhuanlan.zhihu.com/p/21292697

DQN从入门到放弃2 增强学习与MDP

https://zhuanlan.zhihu.com/p/21340755

DQN从入门到放弃3 价值函数与Bellman方程

https://zhuanlan.zhihu.com/p/21378532

DQN从入门到放弃4 动态规划与Q-Learning

https://zhuanlan.zhihu.com/p/21421729

DQN从入门到放弃5 深度解读DQN算法

https://zhuanlan.zhihu.com/p/21547911

DQN从入门到放弃6 DQN的各种改进

https://zhuanlan.zhihu.com/p/21609472

DQN从入门到放弃7 连续控制DQN算法-NAF

https://zhuanlan.zhihu.com/p/56023723

通过Q-learning深入理解强化学习（上）

https://mp.weixin.qq.com/s/0HukwNmg3k-rBrIBByLhnQ

深度Q学习：一步步实现能玩《毁灭战士》的智能体

https://mp.weixin.qq.com/s/x-qCA0TzoVUtZ8VAf8ey0A

深度Q学习介绍

https://mp.weixin.qq.com/s/SqU74jYBrjtp9L-bnBuboA

教你完美实现深度强化学习算法DQN

https://mp.weixin.qq.com/s/Vdt5h8APAFoeVxFYKlywpg

用DeepMind的DQN解数学题，准确率提升15%

https://mp.weixin.qq.com/s/RH4ifA46njdC7fyRI9kVMg

深度Q网络与视觉格斗类游戏

https://mp.weixin.qq.com/s/uymKtR_7IgMpfXcekfkCDg

从强化学习基本概念到Q学习的实现，打造自己的迷宫智能体

https://mp.weixin.qq.com/s/9ZvaZQ1yumhr75okBxNyeA

优化强化学习Q-learning算法进行股市交易

https://mp.weixin.qq.com/s/QkRdv0xMoqwaXsNAMAHR0A

一图尽展视频游戏AI技术，DQN无愧众算法之鼻祖

https://zhuanlan.zhihu.com/p/35882937

强化学习——从Q-Learning到DQN到底发生了什么？

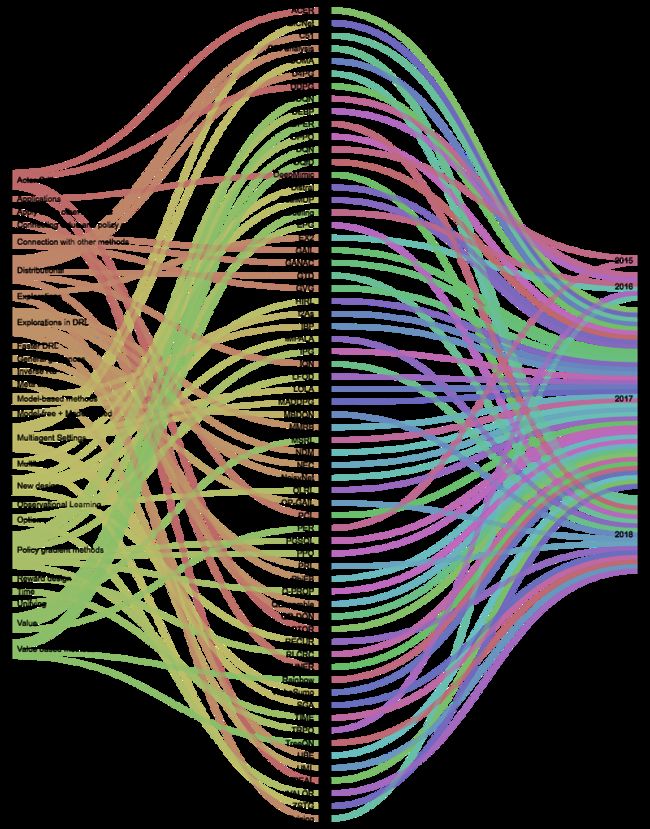
DQN进化史

上图引用自论文：

《Deep Learning for Video Game Playing》

该论文最早发表于2017年，但是作者每年都会更新论文的内容。

---

在Nature DQN出来之后，肯定很多人在思考如何改进它。那么DQN有什么问题呢？

• 目标Q值的计算准确吗？全部通过max Q来计算有没有问题？

• 随机采样的方法好吗？按道理不同样本的重要性是不一样的Q值代表状态，动作的价值，那么单独动作价值的评估会不会更准确？

• DQN中使用$ϵ$-greedy的方法来探索状态空间，有没有更好的做法？

• 使用卷积神经网络的结构是否有局限？加入RNN呢？

• DQN无法解决一些高难度的Atari游戏比如《Montezuma’s Revenge》，如何处理这些游戏？

• DQN训练时间太慢了，跑一个游戏要好几天，有没有办法更快？

• DQN训练是单独的，也就是一个游戏弄一个网络进行训练，有没有办法弄一个网络同时掌握多个游戏，或者训练某一个游戏后将知识迁移到新的游戏？

• DQN能否用在连续动作输出问题？

Double DQN

$$L={\left(r+\gamma Q(s^{\prime },{\mathrm{argmax}}_{a^{\prime }}Q(s^{\prime },a^{\prime },w),w^{-})-Q(s,a,w)\right)}^2$$

Nature DQN的两个Q网络分离的还不够彻底，Double DQN用当前的Q网络来选择动作（公式中红色部分所示），而用目标Q网络来计算目标Q。

参考：

https://mp.weixin.qq.com/s/NkWj1bV7uMjACxAvxhPJXw

DQN系列(1)：Double Q-learning

https://mp.weixin.qq.com/s/WGxodXAxcgsz61VnuSF5aQ

DQN系列(2): Double DQN算法原理与实现

Prioritised replay

采样优先级采用目标Q值与当前Q值的差值来表示：

$$|r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },w^{-})-Q(s,a,w)|$$

优先级越高，那么采样的概率就越高。

Dueling Network

Dueling Network将Q网络分成了两个通道：

• Action无关的值函数：$V(s,v)$

• Action相关的值函数：$A(s,a,w)$

$$Q(s,a)=V(s,v)+A(s,a,w)$$

NAF

传统RL任务：低维输入，低维离散输出。

Atari游戏：高维输入，低维离散输出。

通常的控制系统，除了离散控制之外，还有连续控制，然而DQN并不能直接用于连续域：因为它根本就没办法穷举每一个动作，也就无法计算最大的Q值对应的动作。

论文：

《Continuous Deep Q-Learning with Model-based Acceleration》

对于连续控制，由于我们已经无法选择动作，因此只能设计一种方法，使得我们输入状态，然后能够输出动作，并且保证输出动作对应的Q值是最大值。

这个时候，我们有两种选择：

• 弄两个神经网络，一个是Policy网络，输入状态，输出动作，另一个是Q网络，输入状态，输出Q值。这种做法其实就是Actor-Critic算法。

• 只弄一个神经网络，既能输出动作也能输出Q值。这就是本节所要使用的方法。

在《机器学习（三十五）》中，我们已经指出advantage function不改变策略梯度，但能有效约束variance。这里沿用了A函数定义：

$$A(s,a)=Q(s,a)-V(s)$$

作者设计了如下A函数：

$$A(x,\mu |{\theta }^A)=-\frac{1}{2}(u-\mu (x|{\theta }^{\mu }){)}^{T}P(x|{\theta }^P)(u-\mu (x|{\theta }^{\mu }))$$

其中x是状态，u是动作，$\mu$是神经网络的输出动作。

它的一阶矩阵形式等价于：$A(a)=-P(a-x{)}^2$

因此，这是一个正定二次型的相反数，即$A\le 0$。

我们的目标就是优化A函数，使之尽可能最大（即等于0）。这时A函数对应的动作即为最优动作。

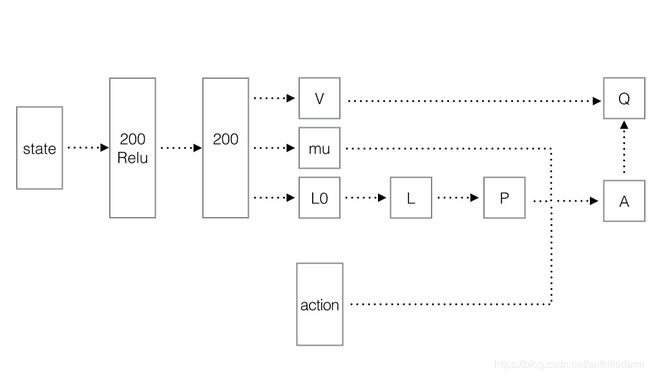
以下是具体的网络结构图。

其流程如下：

• 状态经过两层MLP之后（注意：第2层没有RELU），生成三个tensor：V、$\mu$、L0。

• 将L0转化为L。也就是将一个列向量转换为下三角矩阵，就是从新排列，然后把对角线的数exp对数化。

• 使用Cholesky分解构建P。

若A为n阶对称正定矩阵，则存在唯一的主对角线元素都是正数的下三角阵L，使得$$A=L{L}^T$$，此分解式称为正定矩阵的乔列斯基（Cholesky）分解。

• 按照上图的步骤，依此构建A和Q。其中的Q正好可用于DQN的训练。

综上，NAF既可以输出action，也可产生Q值，而Q值可用于DQN训练，从而使算法可以进行下去。

这里的构造逻辑和VAE很相似，都是假定构造方法成立，然后再用神经网络拟合构造所需的各要素，最后通过训练以达成构造的效果。

Distributional DQN

Distributional DQN也叫做Categorical DQN。

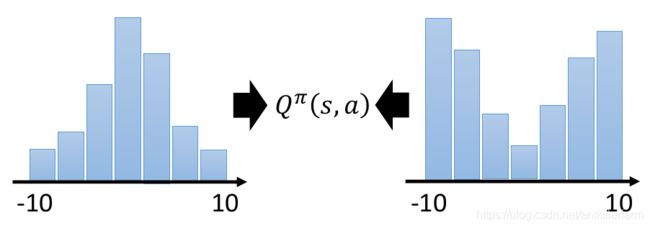
cumulated reward（累计奖励）是一个孤立的值，它无法完全反映reward的全貌，比如上图中的两个reward，其累计值完全相同，但分布却有很大的差异。这一定程度上会对策略的选择产生影响。

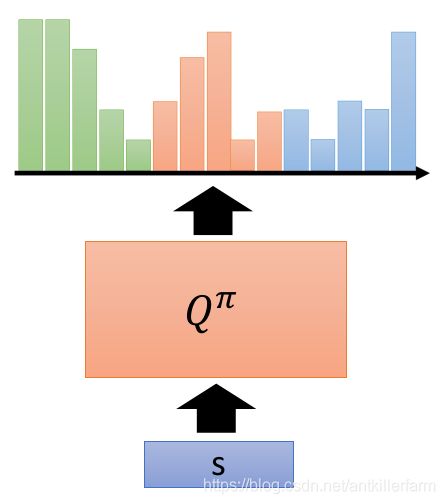
传统DQN最后一层输出的是一个N维的向量，表示N个动作对应的价值，Categorical DQN输出的是N×M维的向量，表示的是N个动作在M个价值分布的支撑上的概率。（以上图为例，N=3，M=5。）

总结一下就是：传统价值函数的目标是近似地估计价值的期望，而Distributional RL的目标是近似地估计价值的分布（概率密度函数）。

Distributional RL不仅可用于DQN，亦可应用于Actor-Critic，这也就是D4PG的主要idea了。

参考：

https://zhang-yi-chi.github.io/2018/09/19/DistributionalRL/

Distributional Reinforcement Learning

Rainbow

论文：

《Rainbow: Combining Improvements in Deep Reinforcement Learning》

Rainbow算是2017年比较火的一篇DRL方面的论文了。它没有提出新方法，而只是整合了6种DQN算法的变种，达到了SOTA的效果。

这6种DQN算法是：

• Double DQN
• Prioritized Experience Replay
• DuelingNet
• NoisyNet
• Distributional DQN(Categorical DQN)
• N-step Learning

参考：

https://mp.weixin.qq.com/s/SZHMyWOXHM8T3zp_aUt-6A

DeepMind提出Rainbow：整合DQN算法中的六种变体

https://github.com/Curt-Park/rainbow-is-all-you-need

手把手教你从DQN到Rainbow

https://zhuanlan.zhihu.com/p/36375292

最前沿：当我们以为Rainbow就是Atari游戏的巅峰时，Ape-X出来把Rainbow秒成了渣！

参考

https://mp.weixin.qq.com/s/o27U97Y7BmMUXe3zAToHSQ

强化学习DQN初探之2048

https://mp.weixin.qq.com/s/SJd-3qH4W4GMMLZSmvFk1w

利用DQN玩吃豆人（Pacman）小游戏

https://mp.weixin.qq.com/s/snNvN4FFP0VEZwDA0TAp1w

强化学习训练Chrome小恐龙Dino Run：最高超过4000分