Yolov5（6.1）学习历险记

目录

YOLO系列总体构架：

CBS模块

torch.nn.Conv2d:对由多个输入平面组成的输入信号进行二维卷积。

Batch Normalization 归一化处理

SiLu（Swish）激活函数

C3模块

Bottleneck：瓶颈层

SPPF（快速空间金字塔池化）

SPP：

 nn.MaxPool2d:最大池化操作 

SPPF ：

YOLO系列总体构架：

 对应到YOLOV5中，具体backbone构架如下：

CBS模块

首先CBS模块在common.py中定义为Class Conv：

class Conv(nn.Module):
    # Standard convolution
    def __init__(self, c1, c2, k=1, s=1, p=None, g=1, act=True):  # ch_in, ch_out, kernel, stride, padding, groups
        super().__init__()
        self.conv = nn.Conv2d(c1, c2, k, s, autopad(k, p), groups=g, bias=False)
        self.bn = nn.BatchNorm2d(c2)
        self.act = nn.SiLU() if act is True else (act if isinstance(act, nn.Module) else nn.Identity())

    def forward(self, x):
        return self.act(self.bn(self.conv(x)))

    def forward_fuse(self, x):
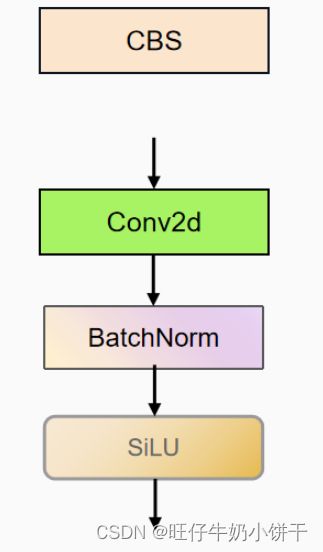
        return self.act(self.conv(x))

 CBS这个名字就很容易理解啦（C代表Conv，B代表BatchNorm2d，S代表SiLu激活函数）。          运算顺序由前向传播def forward来定义：首先对输入信号进行二维卷积（Conv2d）然后到BN层进行归一化处理，将结果传到激活函数部分。之前版本用的是Leaky Relu激活函数，6.X版本换成了SiLu激活函数。

torch.nn.Conv2d:对由多个输入平面组成的输入信号进行二维卷积。

一维卷积卷积核只能在长度方向上进行滑窗操作，二维卷积可以在长和宽方向上进行滑窗操作，三维卷积可以在长、宽以及channel方向上进行滑窗操作。一个卷积核运算一次得到一个值，output channel取决于卷积核的个数。

self.Conv=nn.Conv2d(c1,c2,k,s,autopad(k,p),groups=g,bias=False)                               

c1:输入通道数      c2:输出通道数     

k:卷积核大小        s:步长

autopad:表示需不需要对特征图进行填充。当指定p值时按照p值进行填充，当p值为默认时则通过autopad函数进行填充。                                                                                               

groups：表示分组卷积，g=1时默认使用正常的卷积，大于1则使用分组卷积；                 

dilation：表示是否使用空洞卷积（v5中默认为1不使用）。                                                     

那么！空洞卷积（扩张卷积）可以增加感受野，分组卷积可以减少计算量做到模型轻量化（原理上是这样），具体实践效果可以根据不同的应用场景进行修改。

Batch Normalization 归一化处理

在卷积神经网络的卷积层后一般会添加BatchNorm2d进行数据归一化处理，使数据在进行激活函数非线性处理单元之前不会因为数据过大而导致网络性能不稳定。

目的：使特征图满足均值为0，方差为1的分布规律。对输入batch的每一个特征通道进行Normalize。

nn.BatchNorm2d(num, eps=1e-05, momentum=0.1, affine=True,track_running_stats=True) 

num_features：一般输入参数的shape为batch_size*num_features*height*width，即为其中特征的数量，即为输入BN层的通道数；     

eps：一个辅助计算值，避免计算时出现分母为0的情况；                                                        momentum：用于运算过程中均值和方差的一个估计参数                                                    

affine：当设置为True时，会给定可以学习的系数矩阵gamma和beta。

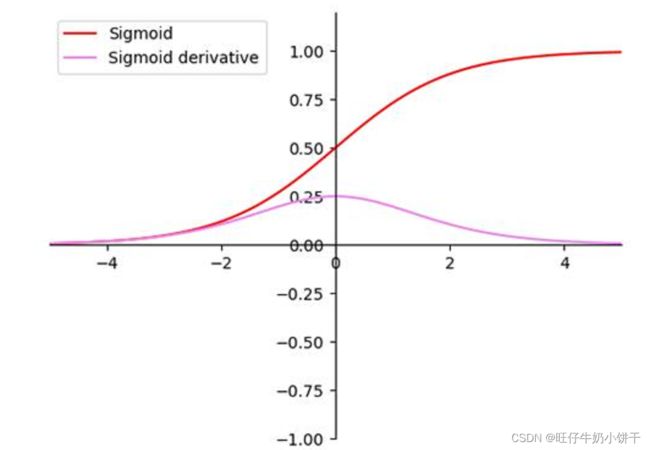
SiLu（Swish）激活函数

激活函数定义：在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。

激活函数使神经网络具有非线性，决定感知机是否激发。这种非线性赋予了深度网络学习复杂函数的能力。如果不使用激活函数，则相当于f（x）=x，这也就是最原始的感知机，即每一层节点的输入都是上层输出的线性函数，使得网络的逼近能力有限。YOLOv5中激活函数实现的相关代码在utils/activations.py中

名称	图像	用途	缺点
Sigmoid		将输入映射（0,1）区间，用来做二分类。对于一个极大的负值输入，它输出的值接近于0；对于一个极大的正值输入，它输出的值接近于1。	反向传播时会存在梯度爆炸和梯度消失现象；且输出不是以0为中心，会降低学习效率。
tanh		tanh可以将输入映射到（-1,1）区间，解决Sigmoid不是以0为中心输出的问题	梯度消失问题和幂运算导致训练时间长
ReLU		ReLU将所有负值取作0，正值保持不变	解决梯度消失问题且收敛速度快。但输出不是以0为中心，且可能某些神经单元永远不会被激活，导致相应参数不能被更新
Leaky ReLU		Leaky ReLU与ReLU很相似，仅在输入小于0的部分，值为负，且有微小的梯度	解决ReLU无效神经元的部分，但效果不一定总是好于ReLU
SiLU		对于较大的值，SiLU 的激活大约等于ReLU的激活。 与 ReLU最大的不同，SiLU 的激活不是单调递增的。	优点：无上界，有下界，平滑 无上界：避免过拟合 有下届：正则化效果更强 平滑：处处可导，容易训练
Mish		在ImageNet上效果比ReLU和Swish都更好	优点：无上界、无下界、光滑、非单调（自身就有正则化效果，使函数更加平滑，更容易泛化）。

 CBS模块结构图：

C3模块

class C3(nn.Module):
    # CSP Bottleneck with 3 convolutions
    def __init__(self, c1, c2, n=1, shortcut=True, g=1, e=0.5):  # ch_in, ch_out, number, shortcut, groups, expansion
        super().__init__()
        c_ = int(c2 * e)  # hidden channels
        self.cv1 = Conv(c1, c_, 1, 1)
        self.cv2 = Conv(c1, c_, 1, 1)
        self.cv3 = Conv(2 * c_, c2, 1)  # act=FReLU(c2)
        self.m = nn.Sequential(*(Bottleneck(c_, c_, shortcut, g, e=1.0) for _ in range(n)))
        # self.m = nn.Sequential(*[CrossConv(c_, c_, 3, 1, g, 1.0, shortcut) for _ in range(n)])

    def forward(self, x):
        return self.cv3(torch.cat((self.m(self.cv1(x)), self.cv2(x)), dim=1))

从代码可以看出，输入分成了俩部分，一部分先经过Cv1在经过self.m定义的Bottleneck操作，另一部分直接经过Cv2，俩部分最后汇总拼接后一起经过Cv3得到输出！其中定义了隐藏通道C_(我的理解就是在最终输出前的那些输出~）self.m操作使用nn.Sequential将n个Bottleneck串接到网络中（具体几个要结合配置文件里的参数计算!即number×depth_multiple个）

Bottleneck：瓶颈层

class Bottleneck(nn.Module):
    # Standard bottleneck
    def __init__(self, c1, c2, shortcut=True, g=1, e=0.5):  # ch_in, ch_out, shortcut, groups, expansion
        super().__init__()
        c_ = int(c2 * e)  # hidden channels
        self.cv1 = Conv(c1, c_, 1, 1)
        self.cv2 = Conv(c_, c2, 3, 1, g=g)
        self.add = shortcut and c1 == c2

    def forward(self, x):
        return x + self.cv2(self.cv1(x)) if self.add else self.cv2(self.cv1(x))

bottleneck layery又叫瓶颈层，在残差网络中提出这个概念。一般在较深的网络中，如resnet101中使用。（可以达到模型轻量化的一个效果）

 a 无Bottleneck                                                    b有Bottleneck

Bottleneck结构就是为了降低参数量，Bottleneck先进行PW（Pointwise Convolution点卷积，即1x1卷积）对数据进行降维，再进行常规卷积核的卷积，最后PW对数据进行升维。

举个例子：直接使用3x3的卷积核。256维的输入直接经过一个3x3x256的卷积层，输出一个256维的特征图，那么参数量为：256（输入）x3x3x256（卷积核） =  589824                      Compare：先经过1x1的卷积核，再经过3x3的卷积核，最后经过一个1x1的卷积核。256维的输入先经过一个1x1x64的卷积层，再经过一个3x3x64的卷积层，最后经过一个1x1x256的卷积层，则总参数量为：256（输入）x1x1x64（卷积核） + 64（输入）x3x3x64（卷积核） + 64（输入）x1x1x256（卷积核） =  69632。

那么在YOLOv5中呢先是1x1的卷积层（CBS)，然后再是3x3的卷积层（CBS），最后通过残差结构与初始输入相加。（add操作通道数不变，concat操作通道数相加）比起原始的Bottleneck结构少了一个1*1卷积的升维操作，因为我们用了Concat！

另外在neck部分的C3操作是没有残差连接的，（shortcut=False，执行self.cv2(self.cv1(x))）

SPPF（快速空间金字塔池化）

SPP：

 在介绍SPPF之前先说SPP（5.X版本用的还是SPP,6.X 版本后作者对其作了改进）

SPP模块是何凯明2015年提出的。主要是为了解决对图像区域裁剪、缩放操作导致的图像失真等问题以及卷积神经网络对图相关重复特征提取的问题。通过此操作可以提高计算效率，节省计算时间。

class SPP(nn.Module):
    # Spatial Pyramid Pooling (SPP) layer https://arxiv.org/abs/1406.4729
    def __init__(self, c1, c2, k=(5, 9, 13)):
        super().__init__()
        c_ = c1 // 2  # hidden channels
        self.cv1 = Conv(c1, c_, 1, 1)
        self.cv2 = Conv(c_ * (len(k) + 1), c2, 1, 1)
        self.m = nn.ModuleList([nn.MaxPool2d(kernel_size=x, stride=1, padding=x // 2) for x in k])

    def forward(self, x):
        x = self.cv1(x)
        with warnings.catch_warnings():
            warnings.simplefilter('ignore')  # suppress torch 1.9.0 max_pool2d() warning
            return self.cv2(torch.cat([x] + [m(x) for m in self.m], 1))

 nn.MaxPool2d:最大池化操作 

卷积操作中池化层提取重要信息的操作，可以去掉不重要的信息，减少计算开销。最大池化操作相当于核在图像上移动的时候，筛选出被核覆盖区域的最大值。目的就是为了保留输入的特征，但是同时把数据量减少，对于整个网路来说，进行计算的参数就变少了，就会训练的更快。

#class _MaxPoolNd(Module):
    __constants__ = ['kernel_size', 'stride', 'padding', 'dilation',
                     'return_indices', 'ceil_mode']
    return_indices: bool
    ceil_mode: bool

#  kernel_size ：表示做最大池化的窗口大小（卷积核大小）            stride ：步长
    padding ：填充        dilation ：控制窗口中元素步幅，扩张操作（空洞卷积）
    return_indices ：布尔类型，返回最大值位置索引
    ceil_mode ：布尔类型，为True，用向上取整的方法，计算输出形状；默认是向下取整。

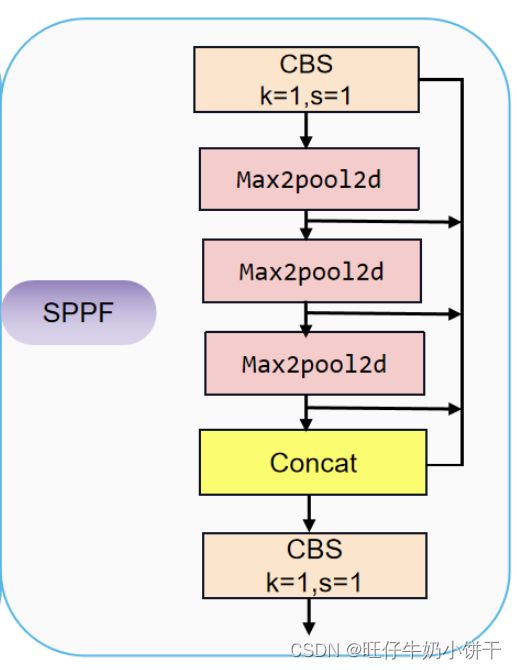
SPPF ：

这个是YOLOv5作者在SPP基础上进行改进，速度比SPP要快很多所以叫SPPF。

class SPPF(nn.Module):
    # Spatial Pyramid Pooling - Fast (SPPF) layer for YOLOv5 by Glenn Jocher
    def __init__(self, c1, c2, k=5):  # equivalent to SPP(k=(5, 9, 13))
        super().__init__()
        c_ = c1 // 2  # hidden channels
        self.cv1 = Conv(c1, c_, 1, 1)
        self.cv2 = Conv(c_ * 4, c2, 1, 1)
        self.m = nn.MaxPool2d(kernel_size=k, stride=1, padding=k // 2)

    def forward(self, x):
        x = self.cv1(x)
        with warnings.catch_warnings():
            warnings.simplefilter('ignore')  # suppress torch 1.9.0 max_pool2d() warning
            y1 = self.m(x)
            y2 = self.m(y1)
            return self.cv2(torch.cat([x, y1, y2, self.m(y2)], 1))

 在这里呢作者首先把最大池化操作的卷积核全部换成了5*5大小，能够达到同样的效果且计算速度更快。其次作者这里借鉴了残差结构，之前SPP模块中在CBS操作后有四个通道而这里通道数减半只有俩个，达到减少计算量的目的。（PS：可以针对这个点对网络结构进行改进~）

那么总体上来说Yolov5 6.1版本backbone构架就是这个样子嘞，改进点当然很多~但是不建议把C3模块全部换掉，一般来说把C3全部改掉多半是会起到负作用的，可以针对Conv卷积进行改进，比如空洞卷积，分组卷积等去达到一个轻量化的效果；在backbone中加入注意力机制模块（一般放在深层比浅层要好，对浅层特征作用不大，并且与模块融合比单独加在某一层效果要好~但具体位置数量还是要根据应用场景进行调整）；针对空间金字塔部分也可以参考资料看看怎么改，去增强对浅层信息和深层信息的一个有机结合！最后祝我有多点tricks！能够早日写出小论文！