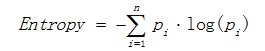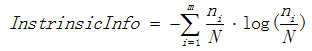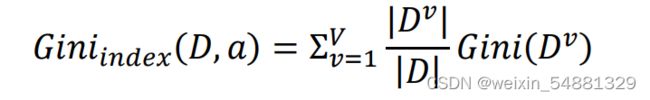决策树的创建与使用决策树进行分类

(一)基本流程

1：什么是决策树？

分类决策树模型是一种描述对实例进行分类的树形结构。 决策树由结点和有向边组成。结点有两种类型：内部结点和叶节点。内部结点表示一个特征或属性，叶节点表示一个类。

例如下图一个例子，现想象一个男孩的母亲要给这个男孩介绍女朋友，决策树用树结构实现上述的判断流程如下图。

 2：决策树的性质

（1）决策树基于树结构来进行预测

（2）决策过程中提出的每个判定问题都是对某个属性的“测试”

（3）每个测试的结果或是导出最终结论，或者导出进一步的判定问题，其考虑范围是在上次决策结果的限定范围之内

（4）从根结点到每个叶结点的路径对应了一个判定测试序列

（5）决策树学习的目的是为了产生一棵泛化能力强， 即处理未见示例能力强的决策树

3：构建决策树的步骤

步骤1：将所有的数据看成是一个节点，进入步骤2；

步骤2：从所有的数据特征中挑选一个数据特征对节点进行分割，进入步骤3；

步骤3：生成若干孩子节点，对每一个孩子节点进行判断，如果满足停止分裂的条件，进入步骤4；否则，进入步骤2；

步骤4：设置该节点是子节点，其输出的结果为该节点数量占比最大的类别。

（二）划分选择

1：决策树学习的关键在于如何选择最优划分属性。

一般而 言，随着划分过程不断进行，我们希望决策树的分支结点 所包含的样本尽可能属于同一类别，即结点的“纯度 ”(purity)越来越高

2：经典的属性划分方法：–信息增益：ID 3

                                          –增益率：C 4.5

                                          –基尼指数：CART

3：信息增益

（1）

 用信息增益表示分裂前后跟的数据复杂度和分裂节点数据复杂度的变化值，计算公式表示为：

　　　　　　　　

                                  　　 

      其中Gain表示节点的复杂度，Gain越高，说明复杂度越高。信息增益说白了就是分裂前的数据复杂度减去孩子节点的数据复杂度的和，信息增益越大，分裂后的复杂度减小得越多，分类的效果越明显。

 

节点的复杂度可以用以下两种不同的计算方式：

　　a）熵

　　熵描述了数据的混乱程度，熵越大，混乱程度越高，也就是纯度越低；反之，熵越小，混乱程度越低，纯度越高。 熵的计算公式如下所示：

                                                         　　　　　　　　

                                   　　　　　　　　　　

　　其中Pi表示类i的数量占比。以二分类问题为例，如果两类的数量相同，此时分类节点的纯度最低，熵等于1；如果节点的数据属于同一类时，此时节点的纯度最高，熵 等于0。

　　b）基尼值

　　基尼值计算公式如下：

                                                    　　　　　　　　　　　　

　　其中Pi表示类i的数量占比。其同样以上述熵的二分类例子为例，当两类数量相等时，基尼值等于0.5 ；当节点数据属于同一类时，基尼值等于0 。基尼值越大，数据越不纯。

（2）信息增益率

      使用信息增益作为选择分裂的条件有一个不可避免的缺点：倾向选择分支比较多的属性进行分裂。为了解决这个问题，引入了信息增益率这个概念。信息增益率是在信息增益的基础上除以分裂节点数据量的信息增益（听起来很拗口），其计算公式如下：

                                                                  　　　　 　　   

         

      其中

 表示信息增益， 表示分裂子节点数据量的信息增益，其计算公式为：

                                                                              

         

      其中m表示子节点的数量，

表示第i个子节点的数据量，N表示父节点数据量，说白了， 其实是分裂节点的熵，如果节点的数据链越接近，越大，如果子节点越大，越大，而就会越小，能够降低节点分裂时选择子节点多的分裂属性的倾向性。信息增益率越高，说明分裂的效果越好。

（3）基尼指数

分类问题中，假设D有K个类，样本点属于第k类的概率为pk; 则概率 分布的基尼值定义为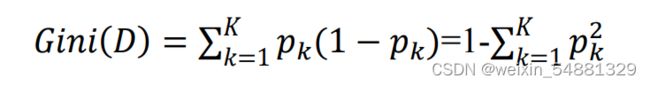： Gini(D)越小，数据集D的纯度越高；

给定数据集D，属性a的基尼指数定义为：

在候选属性集合A中，选择那个使得划分后基尼指数最小的属性作为最有划分属性。

（三）：决策树实现（参考(23条消息) 机器学习 之 尽可能通俗易懂的决策树算法_Dezeming的博客-CSDN博客）

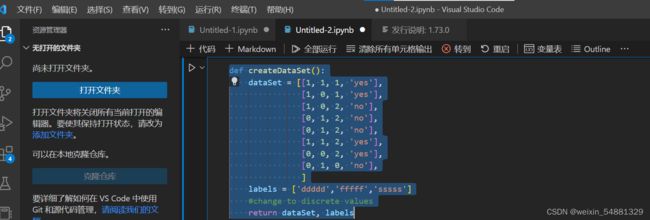
1：生成数据集

 先建立一个数据集，里面每行数据代表一个样本，每个样本的前三个数据代表三个特征，第四个数据代表样本的分类。下面的标签表示每个样本的这三个特征分别是啥

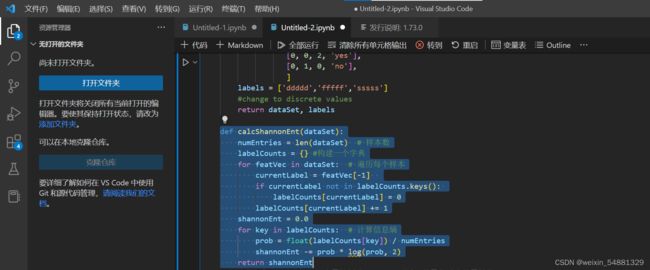
 2：计算信息熵：

首先它输入一个数据集，就用上面的函数返回的dataSet就好了。然后我们先计算出样本数，并采用中括号构建一个字典。然后遍历每个样本，featVec[-1]表示每个样本中的数据的最后一个数据的值，也就是分类用的类别，在我们的数据集里分别是yes和no。如果该类别在字典里没有，则说明是一个新类别，然后我们就让字典包含该类别。然后数值+1。

3： 划分子数据集：axis:按第几个属性划分，value:要返回的子集对应的属性值

4：选择最好的数据集进行划分：dataSet[0]代表第一个样本，即[1, 1, 'yes']，长度为3, 3-1=2，表示该样本的特征数。然后计算出香农熵。

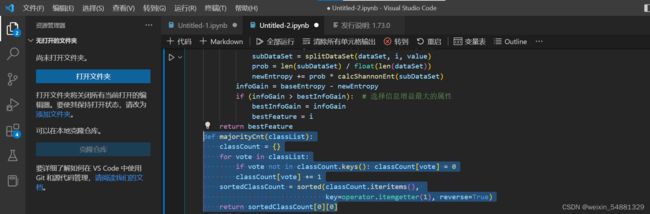
5：通过排序返回出现次数最多的类别：因为每次我们划分数据的时候，都会用掉一个特征来进行划分。用掉的特征以后不会再使用了（因为用一个特征划分好以后，其每个子分支各自的该特征的值都是一样的）。假设在我们不断细分的过程中，发现所有的特征值都用完了所以需要返回当前类别，这个类别就用分到这个树枝的所有类别中比例最大的来代替，即假如分到该树枝的类别中有5个yes，2个no，最后我们就把它作为yes返回。 

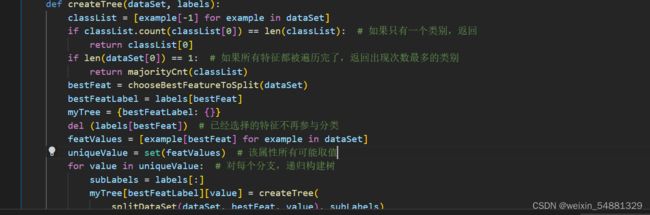
6：构建决策树：

用两个if判断，如果都是属于同一类别的，则直接将该类作为该树枝里的样本所代表的类。如果用于划分的特征都用完了，就直接把该类中数量最多的类别返回。如果没有用完特征并且树枝里有许多别的类别，就继续处理：构建一个树，采用最好的划分特征进行划分。删除该特征的列，然后对每个分支进行递归构建决策树。

 

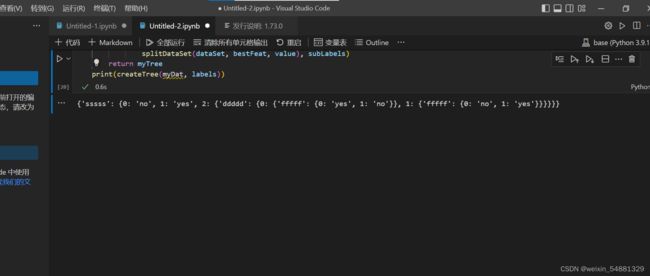
7：最后 print(createTree(myDat, labels)) 测试结果