Python 决策树分类算法分析与实现

决策树分类算法分析与实现

决策树分类算法是最为常见的一种分类算法，通过属性划分来建立一棵决策树，测试对象通过在树上由顶向下搜索确定所属的分类。决策树的构建主要需要解决两个问题：

（1）树的每次成长，选择哪个属性进行划分，可以参考下面几个标准：

A Gini系数

多分支Gini系数的组合方法

B 基于熵的信息增益或信息增益率

熵的定义

信息增益的定义

信息增益率的定义

C 误分率

（2）什么时候在一个节点上停止生长（继续划分），可考虑包含下面两个原则：

A 当节点分配的所有记录都属于同一类时停止

B 当没有属性可以使用时停止

代码：

import numpy as np
'''决策树使用方法
生成实例: clf=DecisionTree()
训练,fit(): clf.fix(X,y). X,y均为np.ndarray类型
预测,predict(): clf.predict(X)
可视化决策树，showTree()

'''
class DecisionTree:
    def __init__(self,mode='C4.5'):
        self._tree=None
        if mode=='C4.5'or mode =='ID3':
            self.mode=mode
        else:
            raise Exception('mode should be C4.5 or ID3')
    def _calcEntropy(self,y):
        """
        计算熵
        :param y: 数据集的标签
        :return: 熵值
        """
        num=y.shape[0]
        labelCounts={}
        for label in y:
            if label not in labelCounts.keys():
                labelCounts[label]=0
            labelCounts[label]+=1
        #计算熵
        entropy = 0.0
        for key in labelCounts:
            weight = float(labelCounts[key])/num
            entropy -= weight* np.log2(weight)
        return entropy
    def _splitDataSet(self,X,y,index,value):
        """
        :param X: 数据集
        :param y: 数据集的标签
        :return: 数据集中特征下标为index,特征值等于value的子数据集
        """
        ret=[]
        featVec=X[:,index]
        X=X[:,[i for i in range(X.shape[1]) if i!=index]]
        for i in range(len(featVec)):
            if featVec[i]==value:
                ret.append(i)
        return X[ret,:],y[ret]

    def _chooseBestFeatureToSplit_ID3(self,X,y):
        """ID3算法计算的是信息增益
        对输入的数据集，选择最佳分割特征
        dataSet:数据集，最后一列为label
        numFeatures:特征个数
        oldEntropy:原始数据集的熵
        newEntropy:按某个特征分割数据集后的熵
        infoGain:信息增益
        bestInfoGain:记录最大的信息增益
        bestFeatureIndex:信息增益最大时，所选择的分割特征的下标
        """
        numFeature = X.shape[1]
        oldEntropy = self._calcEntropy(y)
        bestInfoGain = 0.0
        bestFeatureIndex = -1
        #对每个特征都计算一下信息增益infoGain,并用bestInfoGain记录最大的那个
        for i in range(numFeature):
            featList = X[:,i]
            uniqueVals = set(featList)
            newEntropy = 0.0
            #对第i个特征的各个value，得到各个子数据集，计算各个子数据集的熵
            #进一步地可以计算得到根据第i个特征分割原始数据后的熵newEntropy
            for value in uniqueVals:
                sub_X,sub_y=self._splitDataSet(X,y,i,value)
                prob = len(sub_y)/float(len(y))
                newEntropy += prob * self._calcEntropy(sub_y)
            # 计算信息增益，根据信息增益选择最佳分割特征
            infoGain = oldEntropy-newEntropy
            if(infoGain>bestInfoGain):
                bestInfoGain = infoGain
                bestFeatureIndex = i
        return bestFeatureIndex

    def _chooseBestFeatureToSplit_C45(self,X,y):
        """C4.5算法计算的是信息增益率
        """
        numFeature = X.shape[1]
        oldEntropy = self._calcEntropy(y)
        bestGainRatio = 0.0
        bestFeatureIndex = -1
        #对每个特征都计算一下信息增益率gainRatio=infoGain/splitInformation
        for i in range(numFeature):
            featList = X[:, i]
            uniqueVals = set(featList)
            newEntropy = 0.0
            splitInformation = 0.0
            # 对第i个特征的各个value，得到各个子数据集，计算各个子数据集的熵
            # 进一步地可以计算得到根据第i个特征分割原始数据后的熵newEntropy
            for value in uniqueVals:
                sub_X, sub_y = self._splitDataSet(X, y, i, value)
                prob = len(sub_y) / float(len(y))
                newEntropy += prob * self._calcEntropy(sub_y)
                splitInformation -= prob * np.log2(prob)
            # 计算信息增益率，根据信息增益率选择最佳分割特征
            #splitInformation若为0，说明该特征的所有值都是相同的，不能作为分割特征
            if splitInformation ==0.0:
                pass
            else:
                infoGain = oldEntropy - newEntropy
                gainRatio = infoGain/splitInformation
                if (gainRatio > bestGainRatio):
                    bestGainRatio = gainRatio
                    bestFeatureIndex = i
        return bestFeatureIndex

    def _majorityCnt(self,labelList):
        """返回labelList中出现次数最多的label
        """
        labelCount={}
        for vote in labelList:
            if vote not in labelCount.keys():
                labelCount[vote]=0
            labelList[vote]+=1
        sortedClassCount = sorted(labelCount.items(),key=lambda x:x[1], reverse=True)
        return sortedClassCount[0][0]

    def _createTree(self,X,y,featureIndex):
        """建立决策树
        featureIndex:类型是元组，他记录了X中的特征值在原始数据中对应的下标。
        """
        labelList = list(y)
        #所有label都相同的话，则停止分割，返回该label
        if labelList.count(labelList[0])==len(labelList):
            return labelList[0]
        #没有特征可以分割时，停止分割，返回出现次数最多的label
        if len(featureIndex)==0:
            return self._majorityCnt(labelList)
        #可以继续分割的话，确定最佳分割特征
        if self.mode=='C4.5':
            bestFeatIndex = self._chooseBestFeatureToSplit_C45(X,y)
        elif self.mode=='ID3':
            bestFeatIndex = self._chooseBestFeatureToSplit_ID3(X,y)
        bestFeatStr = featureIndex[bestFeatIndex]
        featureIndex = list(featureIndex)
        featureIndex.remove(bestFeatStr)
        featureIndex = tuple(featureIndex)
        #用字典存储决策树，最佳分割特征作为key,而对应的键值仍然是一棵树（仍用字典存储）
        myTree = {bestFeatStr:{}}
        featValues = X[:,bestFeatIndex]
        uniqueVals = set(featValues)
        for value in uniqueVals:
            #对每个value递归的创建树
            sub_X,sub_y = self._splitDataSet(X,y,bestFeatIndex,value)
            myTree[bestFeatStr][value] = self._createTree(sub_X,sub_y,featureIndex)
        return myTree
    def fit(self,X,y):
        #类型检查
        if isinstance(X,np.ndarray) and isinstance(y,np.ndarray):
            pass
        else:
            try:
                X = np.array(X)
                y = np.array(y)
            except:
                raise TypeError("numpy.ndarray required for X,y")
        featureIndex = tuple(['x'+str(i) for i in range(X.shape[1])])
        self._tree = self._createTree(X,y,featureIndex)
        return self

    def predict(self,X):
        if self._tree==None:
            raise NotFittedError("Estimator not fitted,call 'fit' first")
            # 类型检查
        if isinstance(X, np.ndarray):
            pass
        else:
            try:
                X = np.array(X)
            except:
                raise TypeError("numpy.ndarray required for X")

        def _classify(tree,sample):
            """用训练好的决策树对输入数据分类
            决策树的构建是一个递归的过程，用决策树分类也是一个递归的过程
            _classify()一次只能对一个样本(sample)分类
            """
            featIndex = list(tree.keys())[0]
            secondDict = tree[featIndex]
            key = sample[int(featIndex[1:])]
            valueOfkey = secondDict[key]
            if isinstance(valueOfkey,dict):
                label = _classify(valueOfkey,sample)
            else:
                label = valueOfkey
            return label
        if len(X.shape)==1:
            return _classify(self._tree,X)
        else:
            results = []
            for i in range(X.shape[0]):
                results.append(_classify(self._tree,X[i]))
            return np.array(results)
    def show(self):
        if self._tree == None:
            raise NotFittedError("Estimator not fitted,call 'fit' first")

        print(self._tree)
        createPlot(self._tree)

if __name__ == '__main__':
    # Toy data
    X = [[1, 2, 0, 1, 0],
         [0, 1, 1, 0, 1],
         [1, 0, 0, 0, 1],
         [2, 1, 1, 0, 1],
         [1, 1, 0, 1, 1]]
    y = ['yes', 'yes', 'no', 'no', 'no']

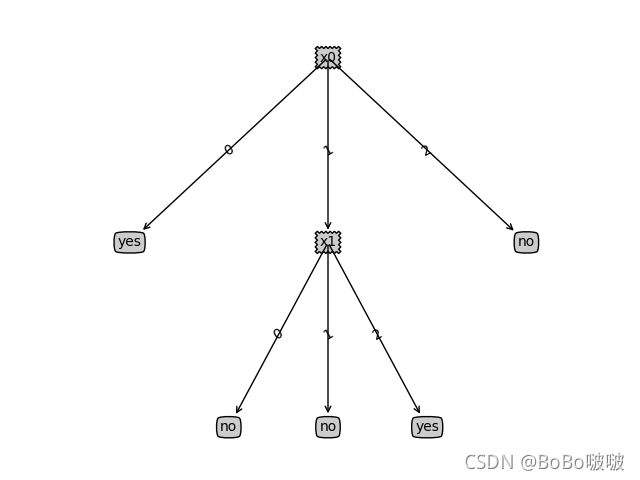
    clf = DecisionTree(mode='ID3')
    clf.fit(X, y)
    clf.show()
    print(clf.predict(X))  # ['yes' 'yes' 'no' 'no' 'no']

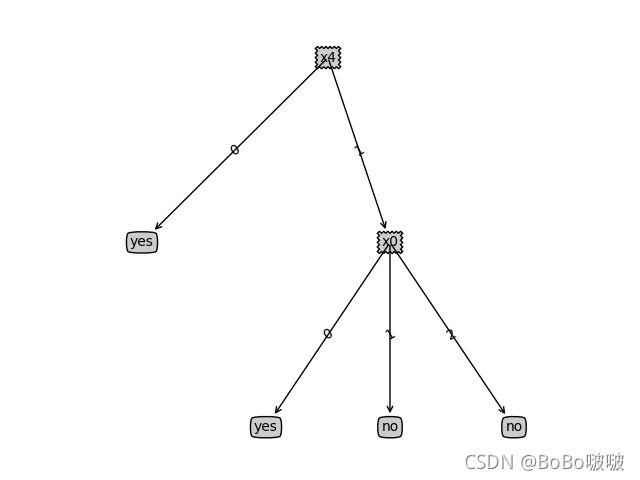
    clf_ = DecisionTree(mode='C4.5')
    clf_.fit(X, y).show()
    print(clf_.predict(X))  # ['yes' 'yes' 'no' 'no' 'no']

可视化Tree需要用到的函数

import matplotlib.pyplot as plt

decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")


def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[
                    key]).__name__ == 'dict':  # test to see if the nodes are dictonaires, if not they are leaf nodes
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[
                    key]).__name__ == 'dict':  # test to see if the nodes are dictonaires, if not they are leaf nodes
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)


def plotTree(myTree, parentPt, nodeTxt):  # if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  # this determines the x width of this tree
    # depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]  # the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[
                    key]).__name__ == 'dict':  # test to see if the nodes are dictonaires, if not they are leaf nodes
            plotTree(secondDict[key], cntrPt, str(key))  # recursion
        else:  # it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


# if you do get a dictonary you know it's a tree, and the first element will be another dict

def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)  # no ticks
    # createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5 / plotTree.totalW;
    plotTree.yOff = 1.0;
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()

结果：

使用ID3算法训练的模型，进行测试的结果

使用C4.5算法训练的模型，进行测试的结果