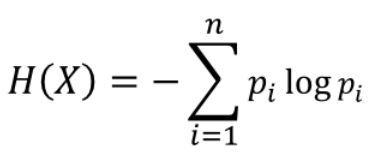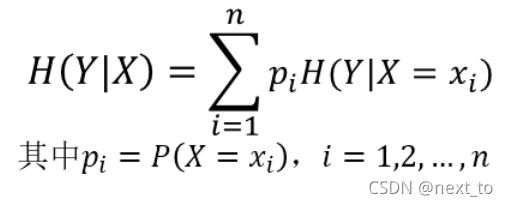人工智能机器学习——西瓜决策树

一、原理

1、介绍

决策树算法是一种逼近离散函数值的方法。 它是一种典型的 分类方法 ，首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策对新数据进行分析。 本质上决策树是通过一系列规则对数据进行分类的过程。 决策树方法最早产生于上世纪60年代，到70年代末。

2、什么是决策树

决策树简单来说就是带有判决规则（if-then）的一种树，可以依据树中的判决规则来预测未知样本的类别和值。

3、定义

定义： 决策树是一个属性结构的预测模型，代表对象属性和对象值之间的一种映射关系。它由节点（node）和有向边（directed edge）组成，其节点有两种类型：内节点（internal node）和叶节点（leafnode），内部节点表示一个特征或属性，叶节点表示一个类。如上图所示的相亲例子，蓝色的椭圆内节点表示的是对象的属性，橘黄色的矩形叶节点表示分类结果（是否相亲），有向边上的值则表示对象每个属性或特征中可能取的值。

4、相关概念

（1）根结点(Root Node)：它表示整个样本集合，并且该节点可以进一步划分成两个或多个子集。

（2）拆分(Splitting)：表示将一个结点拆分成多个子集的过程。

（3）决策结点(Decision Node)：当一个子结点进一步被拆分成多个子节点时，这个子节点就叫做决策结点。

（4）叶子结点(Leaf/Terminal Node)：无法再拆分的结点被称为叶子结点。

（5）剪枝(Pruning)：移除决策树中子结点的过程就叫做剪枝，跟拆分过程相反。

（6）分支/子树(Branch/Sub-Tree)：一棵决策树的一部分就叫做分支或子树。

（7）父结点和子结点(Paren and Child Node)：一个结点被拆分成多个子节点，这个结点就叫做父节点；其拆分后的子结点也叫做子结点。

5、信息增益

（1）熵
在信息论中，熵（entropy）是随机变量不确定性的度量，也就是熵越大，则随机变量的不确定性越大。设X是一个取有限个值得离散随机变量，其概率分布为：

则随机变量X的熵定义为：

（2）条件熵 设有随机变量（X, Y），其联合概率分布为：

条件熵H(Y|X)表示在已知随机变量X的条件下，随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

当熵和条件熵中的概率由数据估计得到时（如极大似然估计），所对应的熵与条件熵分别称为经验熵和经验条件熵。

（3）信息增益 定义：信息增益表示由于得知特征A的信息后儿时的数据集D的分类不确定性减少的程度，定义为：

Gain(D,A) = H(D) - H(D|A)

         即集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(H|A)之差。

二、在jupyter下实现针对西瓜数据集的ID3算法代码

导入西瓜数据集
import numpy as np import pandas as pd import sklearn.tree as st import math data = pd.read_csv('E:\FireFoxDownload\watermalon.txt') data

计算熵

def calcEntropy(dataSet):
    mD = len(dataSet)
    dataLabelList = [x[-1] for x in dataSet]
    dataLabelSet = set(dataLabelList)
    ent = 0
    for label in dataLabelSet:
        mDv = dataLabelList.count(label)
        prop = float(mDv) / mD
        ent = ent - prop * np.math.log(prop, 2)
 
    return ent

拆分数据集

# index - 要拆分的特征的下标
# feature - 要拆分的特征
# 返回值 - dataSet中index所在特征为feature，且去掉index一列的集合
def splitDataSet(dataSet, index, feature):
    splitedDataSet = []
    mD = len(dataSet)
    for data in dataSet:
        if(data[index] == feature):
            sliceTmp = data[:index]
            sliceTmp.extend(data[index + 1:])
            splitedDataSet.append(sliceTmp)
    return splitedDataSet

选择最好的特征

# 返回值 - 最好的特征的下标
def chooseBestFeature(dataSet):
    entD = calcEntropy(dataSet)
    mD = len(dataSet)
    featureNumber = len(dataSet[0]) - 1
    maxGain = -100
    maxIndex = -1
    for i in range(featureNumber):
        entDCopy = entD
        featureI = [x[i] for x in dataSet]
        featureSet = set(featureI)
        for feature in featureSet:
            splitedDataSet = splitDataSet(dataSet, i, feature)  # 拆分数据集
            mDv = len(splitedDataSet)
            entDCopy = entDCopy - float(mDv) / mD * calcEntropy(splitedDataSet)
        if(maxIndex == -1):
            maxGain = entDCopy
            maxIndex = i
        elif(maxGain < entDCopy):
            maxGain = entDCopy
            maxIndex = i
 
    return maxIndex

# 返回值 - 标签
def mainLabel(labelList):
    labelRec = labelList[0]
    maxLabelCount = -1
    labelSet = set(labelList)
    for label in labelSet:
        if(labelList.count(label) > maxLabelCount):
            maxLabelCount = labelList.count(label)
            labelRec = label
    return labelRec

生成树

def createFullDecisionTree(dataSet, featureNames, featureNamesSet, labelListParent):
    labelList = [x[-1] for x in dataSet]
    if(len(dataSet) == 0):
        return mainLabel(labelListParent)
    elif(len(dataSet[0]) == 1): #没有可划分的属性了
        return mainLabel(labelList)  #选出最多的label作为该数据集的标签
    elif(labelList.count(labelList[0]) == len(labelList)): # 全部都属于同一个Label
        return labelList[0]
 
    bestFeatureIndex = chooseBestFeature(dataSet)
    bestFeatureName = featureNames.pop(bestFeatureIndex)
    myTree = {bestFeatureName: {}}
    featureList = featureNamesSet.pop(bestFeatureIndex)
    featureSet = set(featureList)
    for feature in featureSet:
        featureNamesNext = featureNames[:]
        featureNamesSetNext = featureNamesSet[:][:]
        splitedDataSet = splitDataSet(dataSet, bestFeatureIndex, feature)
        myTree[bestFeatureName][feature] = createFullDecisionTree(splitedDataSet, featureNamesNext, featureNamesSetNext, labelList)
    return myTree

# 返回值
# dataSet 数据集
# featureNames 标签
# featureNamesSet 列标签
def readWatermelonDataSet():
    dataSet = data.values.tolist()
    featureNames =['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']
    #获取featureNamesSet
    featureNamesSet = []
    for i in range(len(dataSet[0]) - 1):
        col = [x[i] for x in dataSet]
        colSet = set(col)
        featureNamesSet.append(list(colSet))
    
    return dataSet, featureNames, featureNamesSet

绘制

# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']
 
# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
 
# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")
 
# 箭头样式
arrow_args = dict(arrowstyle="<-")
 
 
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    绘制一个节点
    :param nodeTxt: 描述该节点的文本信息
    :param centerPt: 文本的坐标
    :param parentPt: 点的坐标，这里也是指父节点的坐标
    :param nodeType: 节点类型,分为叶子节点和决策节点
    :return:
    """
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
 
 
def getNumLeafs(myTree):
    """
    获取叶节点的数目
    :param myTree:
    :return:
    """
    # 统计叶子节点的总数
    numLeafs = 0
 
    # 得到当前第一个key，也就是根节点
    firstStr = list(myTree.keys())[0]
 
    # 得到第一个key对应的内容
    secondDict = myTree[firstStr]
 
    # 递归遍历叶子节点
    for key in secondDict.keys():
        # 如果key对应的是一个字典，就递归调用
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        # 不是的话，说明此时是一个叶子节点
        else:
            numLeafs += 1
    return numLeafs
 
 
def getTreeDepth(myTree):
    """
    得到数的深度层数
    :param myTree:
    :return:
    """
    # 用来保存最大层数
    maxDepth = 0
 
    # 得到根节点
    firstStr = list(myTree.keys())[0]
 
    # 得到key对应的内容
    secondDic = myTree[firstStr]
 
    # 遍历所有子节点
    for key in secondDic.keys():
        # 如果该节点是字典，就递归调用
        if type(secondDic[key]).__name__ == 'dict':
            # 子节点的深度加1
            thisDepth = 1 + getTreeDepth(secondDic[key])
 
        # 说明此时是叶子节点
        else:
            thisDepth = 1
 
        # 替换最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth
 
    return maxDepth
 
 
def plotMidText(cntrPt, parentPt, txtString):
    """
    计算出父节点和子节点的中间位置，填充信息
    :param cntrPt: 子节点坐标
    :param parentPt: 父节点坐标
    :param txtString: 填充的文本信息
    :return:
    """
    # 计算x轴的中间位置
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    # 计算y轴的中间位置
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    # 进行绘制
    createPlot.ax1.text(xMid, yMid, txtString)
 
 
def plotTree(myTree, parentPt, nodeTxt):
    """
    绘制出树的所有节点，递归绘制
    :param myTree: 树
    :param parentPt: 父节点的坐标
    :param nodeTxt: 节点的文本信息
    :return:
    """
    # 计算叶子节点数
    numLeafs = getNumLeafs(myTree=myTree)
 
    # 计算树的深度
    depth = getTreeDepth(myTree=myTree)
 
    # 得到根节点的信息内容
    firstStr = list(myTree.keys())[0]
 
    # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
 
    # 绘制该节点与父节点的联系
    plotMidText(cntrPt, parentPt, nodeTxt)
 
    # 绘制该节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
 
    # 得到当前根节点对应的子树
    secondDict = myTree[firstStr]
 
    # 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
 
    # 循环遍历所有的key
    for key in secondDict.keys():
        # 如果当前的key是字典的话，代表还有子树，则递归遍历
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/W
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            # 打开注释可以观察叶子节点的坐标变化
            # print((plotTree.xOff, plotTree.yOff), secondDict[key])
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制叶子节点和父节点的中间连线内容
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
 
    # 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
 
 
def createPlot(inTree):
    """
    需要绘制的决策树
    :param inTree: 决策树字典
    :return:
    """
    # 创建一个图像
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 计算出决策树的总宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    # 计算出决策树的总深度
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2W
    plotTree.xOff = -0.5/plotTree.totalW
    # 初始的y轴偏移量，每次向下或者向上移动1/D
    plotTree.yOff = 1.0
    # 调用函数进行绘制节点图像
    plotTree(inTree, (0.5, 1.0), '')
    # 绘制
    plt.show()
 
dataSet, featureNames, featureNamesSet=readWatermelonDataSet()
testTree= createFullDecisionTree(dataSet, featureNames, featureNamesSet,featureNames)
createPlot(testTree)
 

结果显示：