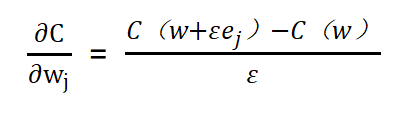为什么反向传播更加高效
理解反向传播有两种方式分别是基于数学式和基于计算图(computational graph),只是理解反向传播的话使用计算图的方法更加直观,但是我认为如果想要了解为什么反向传播效率更高,采用数学式和计算图结合的方式更合适。
下面介绍一下计算图,这一部分内容来自斋藤康毅——《深度学习入门基于python的理论与实现》
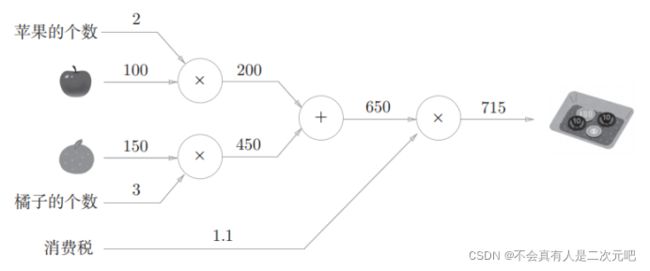
我就不像书中做特别细致的介绍了,很容易的看出来这个图表示的是:100元一个的苹果经过购买2个操作后再收10%的消费税一共花费220元。稍微复杂且更通用的计算图如下图所示:
对于上图来说,得出最终715的结果之前我们都是从左往右一步步的计算,简称为正向传播(forward propagation)。“正向传播是从计算图出发点到结束点的传播。 既然有正向传播这个名称,当然也可以考虑反向(从图上看的话,就是从右向左) 的传播。实际上,这种传播称为反向传播(backward propagation)。”
对于计算图来说,有一个好处是它是局部计算的,无论总的计算有多么复杂,对于某一个节点来说只需要考虑和它相关的一小部分
比如说对于红圈里的节点,无论前面经过了多少计算它只需要关注输入它的650和1.1以及它自身的乘法属性就可以输出715的答案了。
计算图除了可以进行局部运算,使用计算图另一个原因是,可以通过反向传播高效计算导数。
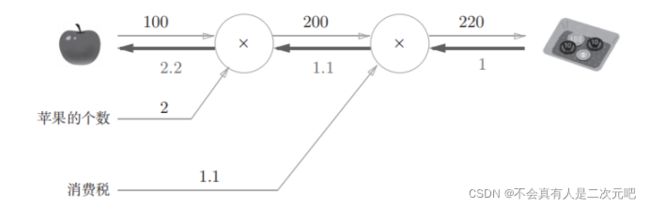
这个图不用多做解释就比较直观了,书中有很详细每一个符号的解释,这个图表示的是从右往左传播了各个节点的导数值。从最右端的支付金额经过中间各个节点最终传到苹果之后值为2.2,就可以理解为支付金额关于苹果的价格的导数的值是2.2。这意味着,如果苹果的价格上涨1元,最终的支付金额会增加2.2元。这1.1和2.2是怎么求出来的呢?书中也讲的很详细了,简单说明一下是因为这里是乘法节点,y=ax求导的值为a是高数的基本公式。把以上内容抽象概括一下可以得出下面的图
这意味着反向传播的值的计算方式是从右往左每经过一个节点就用从右边传过来的值乘上这个节点的偏导数,顺便一提这个E最初的值一般都是1。
以上都是斋藤康毅书中的内容,对计算图进行一个基本的介绍。还有一些关于链式法则的内容就不说了,虽然非常重要但是我觉得大伙应该都会。
书中说完这些内容表示:“通过这样的计算,可以高效地求出导数的值,这是反向传播的要点。”然后对于为什么这样可以高效的求出导数的值就没有更深入的解释了,话锋一转去讲链式法则了,所以我自己看了一些别的资料做出了一点自己的理解:
如果不采用反向传播求导数的话,我们可以用导数最基础的定义去求导数,无论使用何种方法神经网络最终的目标总是让损失函数的值变的更小,神经网络就是自动的调整权值以寻求最小的损失函数的网络,这里把损失函数定义为C(cost)。以下的公式是损失函数对某一个权值w求偏导。这个公式也是导数的定义,ε是一个非常小的值。
但是以上图为例,这种求导方式存在一个问题。假设我们对最下面消费税1.1这个权值求偏导,这里的权值设为![]() 。现在
。现在![]() 发生了细微的变化,我们需要求出这里的导数以发现这里的变化对最终的cost(损失函数)有多大的影响。使用定义法
发生了细微的变化,我们需要求出这里的导数以发现这里的变化对最终的cost(损失函数)有多大的影响。使用定义法 ![]() =
=  ,我们发现用这种方法必须要求得原先
,我们发现用这种方法必须要求得原先![]() 的值,这就要求完整的用正向传播走完全部流程。
的值,这就要求完整的用正向传播走完全部流程。 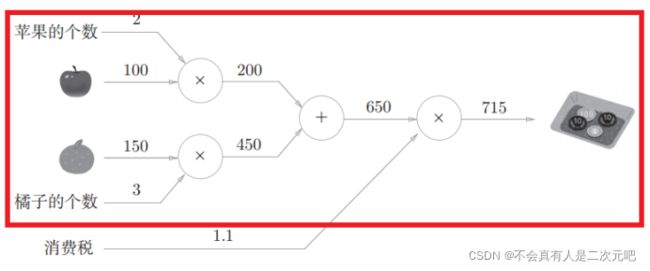
为了求得总的cost即使是一个权值的改变也要完成红色方框里的全部运算
之前提到反向传播的局部运算优点就不会存在这个问题,反向传播只需要考虑自己局部小范围的运算(就是上文提到的E乘以该节点偏导数的例子)。如果一个神经网络有几千几万个权值,每个权值的改变都需要完整的走完整个网络,这就会导致整个网络效率低下,一个权值的改变对它之前的权值都没有关系,如果网络足够复杂对它之后的权值或多或少会有影响,但是正向传播无论如何却同样需要执行几千几万次,这其中有很多是重复计算,这就是为什么反向传播更高效的原因之一。
另外的一个原因跟链式法则有关,也说明了为什么正向传播只能用公式法求导,而不像反向传播可以用公式法求导,现在像跃迁函数,sigmoid函数或者relu函数等经典的激活函数其实表达式都不复杂,可以直接用公式求导的,从这个层面来说套用公式比用导数定义求导也是更方便的。
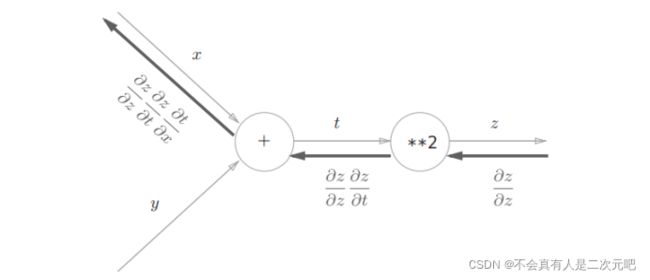
以上图为例,可以从两个方面继续了解反向传播。第一:运用链式法则可以发现我们最终目标是求得损失函数对某一个权值的导数,这张图中以权值x为例,z可以看作是损失函数,因为z在这里已经是最终的函数了,但是这个 中间值其实和x没有关系,无论求多少次都不会有变化,它是从右边传过来的,是可以保存下来避免重复计算的,这是反向传播效率更高的原因其二。第二个方面,为什么正向传播不能像这样整?因为现在我们从左往右看着这张图,还是以x为例,我们会发现当从左往右运算想运用链式法则时,
中间值其实和x没有关系,无论求多少次都不会有变化,它是从右边传过来的,是可以保存下来避免重复计算的,这是反向传播效率更高的原因其二。第二个方面,为什么正向传播不能像这样整?因为现在我们从左往右看着这张图,还是以x为例,我们会发现当从左往右运算想运用链式法则时,![]()
![]() 全是未知的,因为你都没走到那一步,除了预知未来是不能知道这两个值的,不过这个例子中其实
全是未知的,因为你都没走到那一步,除了预知未来是不能知道这两个值的,不过这个例子中其实![]() 是可以知道的,但是如果网络有更深的层,链式法则越来越长就有更多处于中间的偏导数未知,运算是不能进行的,但是采用反向传播的话就没有这个问题了,每一步的值都会前一步的传回去。这也是反向传播的独特的优势。
是可以知道的,但是如果网络有更深的层,链式法则越来越长就有更多处于中间的偏导数未知,运算是不能进行的,但是采用反向传播的话就没有这个问题了,每一步的值都会前一步的传回去。这也是反向传播的独特的优势。