蒙特卡罗方法之三门问题(matlab&python)
目录
一、蒙特卡罗方法
定义
提出
原理
二、三门问题
概述
matlab实现
运行结果
python实现
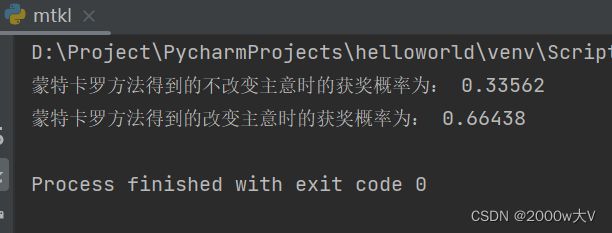
运行结果
一、蒙特卡罗方法
定义
蒙特卡罗方法又称统计模拟法,是一种随机模拟方法,以概率和统计理论方法为基础的⼀种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡罗命名。
提出
蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆和J.冯.诺伊曼首先提出。数学家冯.诺伊曼用驰名世界的赌城——摩纳哥的Monte Carlo——来命名这种方法,为它蒙上了⼀层神秘色彩。在这之前,蒙特卡罗方法就已经存在。1777年,法国Buffffon提出用投针实验的方法求圆周率,这被认为是蒙特卡罗方法的起源。
原理
由大数定理可知,当样本容量足够大时,事件的发生频率即为其概率。
二、三门问题
概述
你参加⼀档电视节目,节目组提供了 ABC 三扇门,主持人告诉你,其中一扇门后边有辆汽车,其它两扇门后是空的。假如你选择了B门 ,这时,主持人打开了 C门 ,让你看到C门 后什么都没有,然后问你要不要改选 A门 ?
matlab实现
%% 代码部分(在成功的条件下的概率)
n = 1000000; % n代表蒙特卡罗模拟重复次数
a = 0; % a表示不改变主意时能赢得汽车的次数
b = 0; % b表示改变主意时能赢得汽车的次数
for i= 1 : n % 开始模拟n次
x = randi([1,3]); % 随机生成一个1-3之间的整数x表示汽车出现在第x扇门后
y = randi([1,3]); % 随机生成一个1-3之间的整数y表示自己选的门
% 下面分为两种情况讨论:x=y和x~=y
if x == y % 如果x和y相同,那么我们只有不改变主意时才能赢
a = a + 1; b = b + 0;
else % x ~= y ,如果x和y不同,那么我们只有改变主意时才能赢
a = a + 0; b = b +1;
end
end
disp(['蒙特卡罗方法得到的不改变主意时的获奖概率为:', num2str(a/n)]);
disp(['蒙特卡罗方法得到的改变主意时的获奖概率为:', num2str(b/n)]);
运行结果
python实现
import numpy as np
n = 100000 # n代表蒙特卡罗模拟重复次数
x = 0 # x表示不改变主意时能赢得汽车的次数
y = 0 # y表示改变主意时能赢得汽车的次数
for i in range(n): #开始模拟n次
a = np.array([1, 2, 3])
b = np.array([1, 2, 3])
c = np.random.choice(a, 1) # 随机生成一个1-3之间的整数c表示汽车出现在第x扇门后
d = np.random.choice(b, 1) # 随机生成一个1-3之间的整数d表示自己选的门
if c == d: # 如果c和d相同,那么我们只有不改变主意时才能赢
x = x + 1
else: # 如果c和d不同,那么我们只有改变主意时才能赢
y = y + 1
print("蒙特卡罗方法得到的不改变主意时的获奖概率为:",x/n)
print("蒙特卡罗方法得到的改变主意时的获奖概率为:",y/n)