用蒙特卡洛算法求解三门问题

一、问题

三个门中其中一扇门后有奖品，参赛者首先选择一扇门，然后主持人打开一扇既没有奖品又没有被参赛者选择的门，然后还剩下一扇门，请问参赛者为了中奖，是应该继续选择之前那扇门，还是应该换另一扇门，还是两者都没有区别。

二、思路分析

用蒙特卡洛算法实现，蒙特卡罗算法一般分为三个步骤，包括构造随机的概率的过程，从构造随机概率分布中抽样，求解估计量。训练10万次，记录不换门的中奖次数和换门的中奖次数。

三、代码实现

import random

s1, s2 = 0, 0

运行10万次

N = 100000
for i in range(0, N):
# 定义三个门，0为无，1为有
door = [0, 0, 0]
# 随机放入一个奖品
door[random.randint(0, 2)] = 1
# 选定一扇门
choose = random.randint(0, 2)
# 打开的没有奖品的门
openDoor = random.randint(0, 2)
# 选择的门和有奖品的门不能被打开
# 如果选中了选择的门和有奖品的门
# 则再次随机选门
while choose == openDoor or door[openDoor] == 1:
openDoor = random.randint(0, 2)
# 不换门的中奖次数累加
if door[choose] == 1:
s1 += 1
# 换门的中奖次数累加
else:
s2 += 1
print(“不换门的中奖概率” + str(s1 / N))
print("换门的中奖概率 " + str(s2 / N))
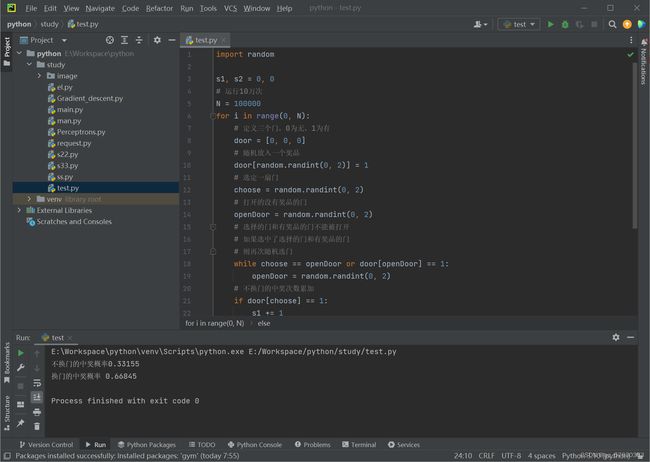
四、实验截图