【20210914】【机器/深度学习】一种非线性降维的手段——manifold learning流形学习

一、背景

        高维数据不像 2-3 维数据那么容易可视化，它很难通过图表展示数据本身的内部结构。所以为了实现数据集结构的可视化，数据的维度必须通过某种方式降维。

二、常用的降维手段

        一系列监督或非监督的线性降维框架，如：Principal Component Analysis(PCA, 主成分分析)、Independent Component Analysis(独立成分分析)、Linear Discriminant Analysis(线性判别分析)……这些方法用于多维数据选择有趣的线性投影，不过会错失数据结构中的非线性项。

        Manifold Learning 是一种非线性降维手段：它从数据本身学习高维结构，不需要使用既定的分类。

        Manifold Learning 是可视化高维数据的工具，它将数据点之间的相似性转换为联合概率，并尝试最小化低维嵌入和高维数据的联合概率之间的 Kullback-Leibler 差异。如果特征的数量非常多，建议是用另一种降维方法，例如：对于密集数据使用 PCA，对于稀疏数据使用 TruncatedSVD，将尺寸数量减少到合理的数量，这将抑制一些噪声并加快样本之间成对距离的计算。

三、用法

        使用 sklearn.manifold.TSNE，这个函数用途：是将特征弄成一坨，变成一个变量，然后和聚类后的 label 画图就可以了。

        （参考：sklearn.manifold.TSNE可视化高位数据工具）

        （参考：基于sklearn.manifold的 T-SNE 的简单使用（介绍关系数据和图像数据）+ matplotlib的简单使用）

''' 导入所需包 '''
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.manifold import TSNE

''' 导入数据集 '''
X = load_iris().data
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans.fit(X)

labels = kmeans.labels_  # 预测标签
labels = pd.DataFrame(labels, columns={'labels'})
X = pd.DataFrame(X)
X.insert(4, 'labels', labels)   # 数据加预测标签一共5列

''' 数据降维 '''
tsne = TSNE()
a = tsne.fit_transform(X)   # 对X进行降维，n_cn_components默认为2，所以a是两列的dataframe数据
liris = pd.DataFrame(a, index=X.index)  # liris也是两列的dataframe数据

d1 = liris[X['labels']==0]  # 降维之后X预测标签为0的数据
d2 = liris[X['labels']==1]  # 降维之后X预测标签为1的数据
d3 = liris[X['labels']==2]  # 降维之后X预测标签为2的数据 
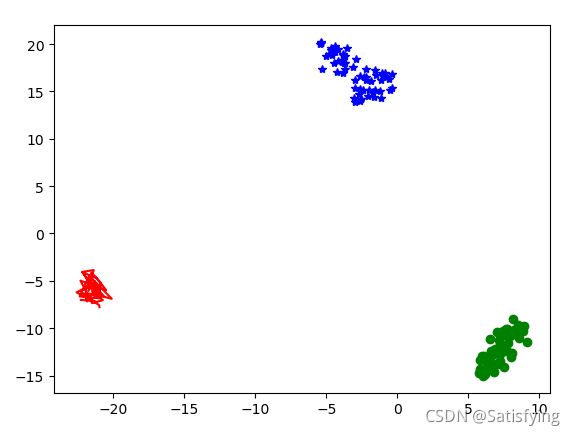
plt.plot(d1[0], d1[1], 'r', d2[0], d2[1], 'go', d3[0], d3[1], 'b*')
plt.show()

四、补充 Tips

        在实现不同标签数据的可视化时，我使用了 scatter 作图工具，它可以指定每类散点的颜色，指定 color 即可~

''' myData 是特征数据，对应的 labels 有两种标签：0 和 1 '''

from sklearn.manifold import TSNE

dic = {'1': 'red', '0': 'blue'}
colors = [dic[str(int(item[0]))] for item in labels.values]

# 二维
tsne_2 = TSNE()
data_embedded_2 = pd.DataFrame(tsne_2.fit_tranform(myData))
plt.figure()
plt.scatter(data_embedded_2.loc[:, 0], data_embedded_2.loc[:, 1], c=colors)
plt.show()

# 三维
tsne_3 = TSNE(n_components=3)
data_embedded_3 = pd.DataFrame(tsne_3.fit_tranform(myData))
plt.figure()
plt.scatter(data_embedded_3.loc[:, 0], data_embedded_3.loc[:, 1], data_embedded_3.loc[:, 2], c=colors)
plt.show()