【Python】用 Python 的 scipy 包实现线性规划(LP)
文章目录
- 一、线性规划(linear programming,LP)
- 二、用 python 实现线性规划
-
- 1. 方法:使用 scipy 包中的 optimize.linprog
- 2. 实例
- 参考链接
一、线性规划(linear programming,LP)
线性规划的标准形式如下:
- 求的是 min
- 所有的约束为 <= 的形式
- 所有的变量均 >=0
如何变为标准形式?
- 原来是max, 直接乘以 -1求min
- 若原来约束为 = ,转为 >= 且 <=(写两个式子,同时成立相当于 = )
- 约束原来为 >= 同样的乘以 -1,就变成了 <=
- 若有变量 xi < 0 ,那么用 x1 – x2来替代,其中x1>=0, x2>=0
二、用 python 实现线性规划
1. 方法:使用 scipy 包中的 optimize.linprog
python真的是非常强大。其 scipy 包里面包含了很多科学计算相关的模块方法。
官方文档:scipy.optimize.linprog
- 函数调用方法:
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='interior-point', callback=None, options=None, x0=None)
- 函数解释:
线性规划:最小化受线性等式和不等式约束的线性目标函数。
-
线性规划解决以下形式的问题:
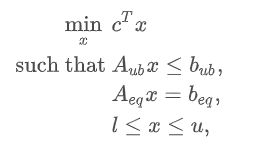
其中 x 为决策变量的向量;c、bub、beq、l 、u是向量;Aub 和 Aeq 是矩阵。 -
参数 method :“interior-point”(默认)、“highs”、“highs-ds”、“highs-ipm”、“revised simplex”、and “simplex” (legacy)
2. 实例
原题目:
有2000元经费,需要采购单价为50元的若干桌子和单价为20元的若干椅子,你希望桌椅的总数尽可能的多,但要求椅子数量不少于桌子数量,且不多于桌子数量的1.5倍,那你需要怎样的一个采购方案呢?
解:要采购x1张桌子,x2把椅子,形式化为:
max z= x1 + x2
s.t. x1 - x2 <= 0
1.5x1 >= x2
50x1 + 20x2 <= 2000
x1, x2 >=0
代码:
from scipy import optimize as opt
import numpy as np
# 参数
# c是目标函数里变量的系数
c = np.array([1, 1])
# a是不等式条件的变量系数
a = np.array([[1, -1], [-1.5, 1], [50, 20]])
# b是不等式条件的常数项
b = np.array([0, 0, 2000])
# a1,b1是等式条件的变量系数和常数项,这个例子里无等式条件,不要这两项
# a1=np.array([[1,1,1]])
# b1=np.array([7])
# 限制
lim1 = (0, None) # (0,None)->(0,+无穷)
lim2 = (0, None)
# 调用函数
ans = opt.linprog(-c, a, b, bounds=(lim1, lim2), method = "interior-point")
# 输出结果
print(ans)
输出结果:
con: array([], dtype=float64)
fun: -62.49999900611857 # 目标函数的最优值
message: 'Optimization terminated successfully.' # 算法退出状态的字符串描述符
nit: 5 # 在所有阶段执行的迭代总数
slack: array([ 1.24999998e+01, -3.33121619e-09, 3.18441803e-05])
status: 0 # 表示算法的退出状态:0: 优化成功终止。1:达到迭代限制。2: 问题似乎是不可行的。3: 问题似乎是无限的。4: 遇到数值困难。
success: True # 当算法成功找到最优解时,为True
x: array([24.9999996 , 37.49999941]) # 在满足约束条件的同时最小化目标函数的决策变量的值
由于解的数量不能为小数,所以最终采购 25 把桌子、37 把椅子(x)。总共采购 62 件(fun)。
参考链接
- 机器学习-线性规划(LP)