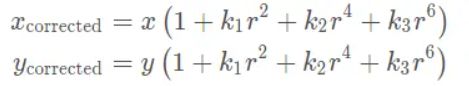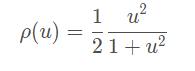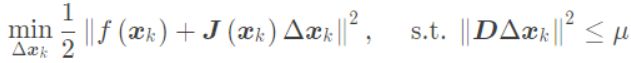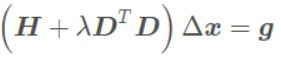SLAM

[TOC]

SLAM面经汇总

SLAM通识基础

视觉SLAM方法的分类和对应的特点分析

视觉SLAM可以分为特征点法和直接法。特征点法是根据提取、匹配特征点来估计相机运动，优化的是重投影误差，对光照变化不敏感，是比较成熟的方案，常见的开源方法有ORB-SLAM等。

特征点法的优点：

（1）特征点本身对光照、运动、旋转比较不敏感，因此稳定性更好。

（2）相机运动较快，也能跟踪成功，鲁棒性较好。

（3）研究时间较久，方案比较成熟。

特征点法的缺点：

（1）关键点提取、描述子匹配时间长。

（2）特征点丢失的场景无法使用。

（3）只能构建稀疏地图。

直接法根据相机的亮度信息估计相机的运动，可以不需要计算关键点和描述子，优化的是光度误差，根据使用像素可分为稀疏、半稠密、稠密三种，常见的方案是SVO、LSD-SLAM等。

直接法的优点：

（1）速度快，可以省去计算特征点和描述子时间。

（2）可以在特征缺失的场合，特征点法在该情况下会急速变差。

（3）可以构建半稠密乃至稠密地图。

直接法的缺点：

（1）因为假设了灰度不变，所以易受光照变化影响。

（2）要求相机运动较慢或采样频率较高。

（3）单个像素或像素块区分度不强，采用的是数量代替质量的策略。

视觉SLAM框架及组成

请描述视觉SLAM的框架以及各个模块的作用是什么？

（1）传感器信息读取。在视觉SLAM中主要是相机图像信息的读取和预处理，在机器人中，还会有码盘、惯性传感器等信息的读取和同步。

（2）视觉里程计就是前端，其任务是估算相邻图像间相机运动，以及局部地图的样子。

（3）后端优化。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。

（4）回环检测。判断机器人是否到达过去先前的位置，如果检测到回环，它会把信息提供给后端进行检测。

（5）建图。根据估计的轨迹，建立与任务要求对应的地图。

激光SLAM中的具体方法有什么？请解释一下每种方法的特点。

激光雷达分为单线和多线两种，单线雷达一般应用在平面运动场景，多线雷达应用在三维运动场景。

（1）单线雷达构建二维地图的SLAM算法称为2D lidar SLAM，包括Gmapping、hector、karto和cartographer算法，在二维平面内运动，扫描平面与运动平面平行。

Gmapping是一种基于粒子滤波的2D激光雷达SLAM，构建二维栅格地图。融合里程计信息，没有回环检测。优点是在小场景中，计算量小，速度较快。 缺点是每个粒子都携带一幅地图，无法应对大场景（内存和计算量巨大）；如果里程不准或标定参数不准，在长回廊等环境中容易把图建歪。

hector SLAM是完全基于scan-matching的，使用迭代优化的方法来求匹配的最佳位置，为避免陷入局部极值，也采用多分辨率的地图匹配。 由于完全依赖于scan matching，要求雷达的测量精度较高、角度范围大，扫描速度较高（或移动速度慢）。噪声多、边角特征点少的场景就很容易失败。 原文所提出方法的特点还在于，加入IMU，使用EKF估计整体的6DoF位姿，并根据roll, pitch角将激光扫描数据投影到XY平面，因而支持激光雷达有一定程度的倾斜，比如手持或机器人运动在不是很平整的地面上。

karto是基于scan-matching，回环检测和图优化SLAM算法，采用SPA（Sparse Pose Adjustment）进行优化。

cartographer是谷歌开源的激光SLAM框架，主要特点在于： 1.引入submap，scan to submap matching，新到的一帧数据与最近的submap匹配，放到最优位置上。如果不再有新的scan更新到最近的submap，再封存该submap，再去创建新的submap。 2.回环检测和优化。利用submap和当前scan作回环检测，如果当前scan与已经创建的submap在距离上足够近，则进行回环检测。检测到回环之后用ceres进行优化，调整submap之间的相对位姿。为了加快回环检测，采用分枝定界法。

（2）3D lidar SLAM算法是针对多线雷达的SLAM方法，包括LOAM、Lego-LOAM和LOAM-livox等。

LOAM是针对多线激光雷达的SLAM算法，主要特点在于：1) 前端抽取平面点和边缘点，然后利用scan-to-scan的匹配来计算帧间位姿，也就形成了里程计；2) 由估计的帧间运动，对scan中的每一个点进行运动补偿；3) 生成map时，利用里程计的信息作为submap-to-map的初始估计，再在利用submap和map之间的匹配做一次优化。 LOAM提出的年代较早（2014），还没有加入回环优化。

LeGO-LOAM在LOAM的基础上主要改进：1) 地面点分割，点云聚类去噪；2）添加了ICP回环检测和gtsam优化。

LOAM_livox是大疆2019年公布的面向小FOV Lidar的LOAM算法。相比LOAM，做了一些改动。算法的特点： 1.添加策略提取更鲁棒的特征点：a) 忽略视角边缘有畸变的区域; b) 剔除反射强度过大或过小的点 ; c) 剔除射线方向与所在平台夹角过小的点; d) 部分被遮挡的点 2.与LOAM一样，有运动补偿 3.里程计中剔除相对位姿解算后匹配度不高的点（比如运动物体）之后，再优化一次求解相对位姿。

刚体运动

相似变换、仿射变换、射影变换的区别是什么？

解答1

相似变换相当于等距变换和均匀缩放的一个复合，用S表示变换矩阵，S为3×3矩阵， $$ \mathrm{S}=\left{\left{\mathrm{s}^* \mathrm{r} 11, \mathrm{S}^* \mathrm{r} 12, \mathrm{tx}\right},\left{\mathrm{s}^* \mathrm{r} 21, \mathrm{s}^* \mathrm{r} 22, \mathrm{ty}\right},{0,0,1}\right} $$ 左上角2×2矩阵为旋转部分，tx和ty为平移因子，具有4个自由度，即旋转、x方向平移、y方向平移和缩放因子s。相似变换前后长度比，夹角，虚圆点I，J保持不变。

仿射变换相当于一个平移变换和一个非均匀变换的复合，用A矩阵表示，A为3×3矩阵， $$ \mathrm{A}={{\mathrm{a} 11, \mathrm{a} 12, \mathrm{tx}},{\mathrm{a} 21, \mathrm{a} 22, \mathrm{ty}},{\mathrm{0}, \mathrm{0}, 1}} $$ 其中A可以分解为： $$ \mathrm{A}=\mathrm{R}(\mathrm{a}) \mathrm{R}(-\mathrm{b}) \mathrm{DR}(\mathrm{b}) $$ 其中 $$ \mathrm{D}={{\mathrm{c} 1, \mathrm{0}},{\mathrm{0}, \mathrm{c} 2}} $$

左上角2×2矩阵为旋转部分，tx和ty为平移因子，它有6个自由度，即旋转4个，x方向平移，y方向平移。它能保持平移性，不能保持垂直性，图像中各部分变换前后面积比保持不变，共线线段或者平行线段的长度比保持不变，矢量的线性组合不变。

射影变换由有限次中心射影的面积定义的两条直线间的对应变换称为一维射影变换，由有限次中心射影的面积定义的两个平面之间的对应变换称为二维射影变换。射影变换是最一般的线性变换，有8个自由度，保持重合关系和交比不变，但不会保持平行性。

解答2

• 等距变换：相当于是平移变换（t）和旋转变换（R）的复合，等距变换前后长度，面积，线线之间的角度都不变。自由度为6（3+3）
• 相似变换：等距变换和均匀缩放（sR,R是正交矩阵，s是缩放因子）的一个复合，类似相似三角形，体积比不变。自由度为7（6+1）
• 仿射变换：一个平移变换（t）和一个非均匀变换（A）的复合，A是可逆矩阵，并不要求是正交矩阵，仿射变换的不变量是:平行线，平行线的长度的比例，面积的比例。自由度为12（9+3）
• 射影变换：当图像中的点的齐次坐标的一般非奇异线性变换，射影变换就是把理想点（平行直线在无穷远处相交）变换到图像上，射影变换的不变量是:重合关系、长度的交比。自由度为15（16-1）

参考：多视图几何总结——等距变换、相似变换、仿射变换和射影变换

给一张图片，知道相机与地面之间的相对关系，计算出图的俯视图。

简单地说利用射影变换，将原本不垂直的线垂直化（用多视图几何上的话说就是消除透视失真），如下图所示 ...

参考：47. 给一张图片，知道相机与地面之间的相对关系，计算出图的俯视图。

四元数的相关概念是什么，请解释一下。

四元数在程序中使用很广泛，但在SLAM中四元数的概念比较难理解。四元数是Hamilton找到的一种扩展复数，四元数具有一个实部和三个虚部： $$ \mathbf{q}=q 0+q 1 i+q 2 j+q 3 k $$ 其中i,j,k是四元数的三个虚部，满足下式： $$ \left{\begin{array}{l} i^2=j^2=k^2=-1 \ i j=k, j i=-k \ j k=i, k j=-i \ k i=j, i k=-j \end{array}\right. $$ 也可以使用标量和向量来表示四元数： $$ \mathbf{q}=[s, \mathbf{v}], \quad s=q_0 \in \mathbb{R}, \mathbf{v}=\left[q_1, q_2, q_3\right] \in \mathbb{R}^3 $$ 在上式中，标量s是四元数的实部，向量v是虚部。

四元数可以表示三维空间中任意一个旋转，与旋转矩阵类似，假设某个旋转是围绕单位向量 $$ \mathbf{n}=[n x, n y, n z] \mathbf{T} $$ 进行了角度为θ的旋转，则该旋转的四元数形式为： $$ \mathbf{q}=\left[\begin{array}{c}
\cos \frac{\theta}{2}, n_x \sin \frac{\theta}{2}, n_y \sin \frac{\theta}{2}, n_z \sin \frac{\theta}{2} \end{array}\right]^T $$ 上式实质上是模长为1的四元数，也就是单位四元数。反之，也可以通过任意长度为1的四元数计算对应旋转轴和夹角： $$ \left{\begin{array}{l} \theta=2 \arccos q_0 \ {\left[n_x, n_y, n_z\right]^T=\left[q_1, q_2, q_3\right]^T / \sin \frac{\theta}{2}} \end{array}\right. $$ 如果某个四元数的长度不为1，可以通过归一化转化为模长为1的四元数。

对四元数的θ加上2π，就可以得到相同旋转，但对应的四元数变为-q。因此，在四元数中，任意的旋转都可以由两个互为相反数的四元数表示。如果θ为0的话，则得到一个没有任何旋转的四元数： $$ \mathbf{q}_0=[\pm 1,0,0,0]^T $$

坐标系转换

世界坐标系（world） 相机坐标（camera） 像素坐标（pixel）

world —— camera：$P c=T c w * P w$

camera —— world：$P w=T c w^{-1} * P c$

pixel —— camera：

$u=f x * X c / Z c+C x ; v=f y * Y c / Z c+C y$

camera —— pixel：

$X c=(u-C x) * Z c / f x ; Y c=(v-C y) * Z c / f y ; Z c=d$

求导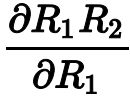

相机模型

相机传感器的分类及其优缺点是什么

视觉SLAM常用的相机包括单目相机、双目相机和深度相机。

单目相机的优点：

（1）应用最广，成本可以做到非常低。

（2）体积小，标定简单，硬件搭建也简单。

（3）在有适合光照的情况下，可以适用于室内和室外环境。

单目相机的缺点：

（1）具有纯视觉传感器的通病：在光照变化大，纹理特征缺失、快速运动导致模糊的情况下无法使用。

（2）SLAM过程中使用单目相机具有尺度不确定性，需要专门的初始化。

（3）必须通过运动才能估计深度，帧间匹配三角化。

双目相机一般有Indemind、小觅和ZED等。

双目相机的优点：

（1）相比于单目相机，在静止时就可以根据左右相机视差图计算深度。

（2）测量距离可以根据基线调节。基线距离越大，测量距离越远。

（3）在有适合光照的情况下，可以适用于室内和室外。

双目相机的缺点：

（1）双目相机标定相对复杂。

（2）用视差计算深度比较消耗资源。

（3）具有纯视觉传感器的通病：在光照变化较大、纹理特征缺失、快速运动导致模糊的情况下无法使用。

深度相机一般有Kinect系列、Realsense系列、Orbbec和Pico等。

深度相机的优点：

（1）使用物理测距方法测量深度，避免了纯视觉方法的通病，适用于没有光照和快速运动的情况。

（2）相对双目相机，输出帧率较高，更适合运动场景。

（3）输出深度值比较准，结合RGB信息，容易实现手势识别、人体姿态估计等应用。

深度相机的缺点：

（1）测量范围窄，容易受光照影响，通常只能用于室内场景。

（2）在遇到投射材料、反光表面、黑色物体情况下表现不好，造成深度图确实。

（3）通常分辨率无法做到很高，目前主流的分辨率是640×480.

（4）标定比较复杂。

单目，双目，深度相机对比

单目：成本低，搭建简单，单目相机有尺度不确定性，需要专门初始化

双目：不需要专门初始化，能够计算深度，基线距离越大，测量距离越远，可以用于室内和室外，标定较为复杂，视差计算比较消耗资源

深度：测量范围窄，噪声大，易受日光干扰，无法测量透射材料，主要用于室内

RGB-D的SLAM和RGB的SLAM有什么区别？

解释相机内外参数

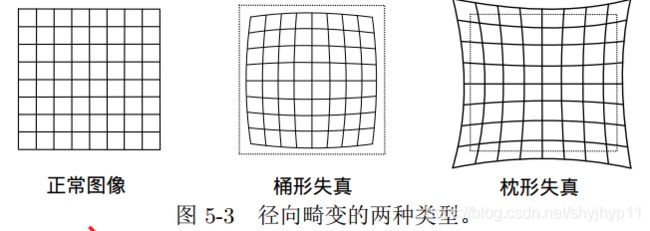
相机内参包括焦距fx，fy，cx，cy，径向畸变系数k1,k2,k3，切向畸变系数p1,p2

其中内参一般来说是不会改变，但是当使用可变焦距镜头时每次改变焦距需要重新标定内参

当图像裁剪时内参cx，cy会发生改变，比如图像从8 * 8变成4 * 4时，cx，cy需要除以2

一般标定工业相机时只需要得到畸变系数k1，k2即可，对于畸变系数较大的鱼眼相机需要得到k3，p1，p2

相机外参分为旋转矩阵R和平移矩阵t，旋转矩阵和平移矩阵共同描述了如何把点从世界坐标系

转换到摄像机坐标系

写出单目相机的投影模型，畸变模型

投影模型一般应该都知道写，但是畸变模型就不一定了…参考《视觉SLAM十四讲》

投影模型如下：

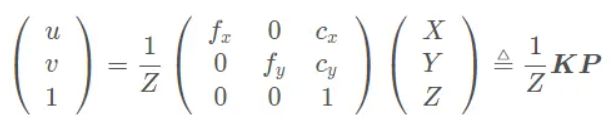注意啊，这里空间点（相机坐标系下的3D点坐标)是非齐次坐标，而像素变成了齐次坐标，如果空间点也是齐次坐标的话，需要讲变换矩阵写成3×4的矩阵，最后一列全为0;。

畸变模型如下：

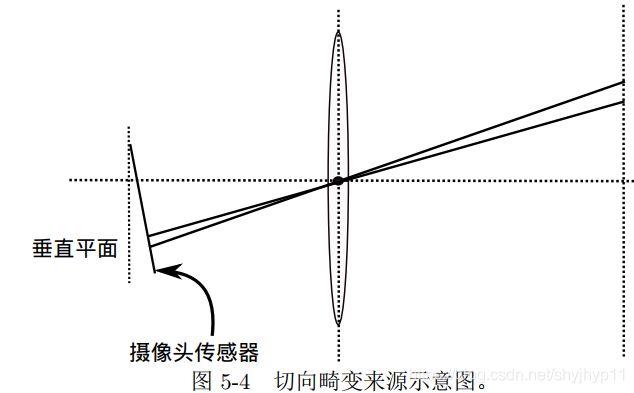
(以下参数含义：平面上的任意一点 p 可以用笛卡尔坐标表示为 [x,y]^T , 也可以把它写成极坐标的形式[r,θ]^T，其中 r 表示点 p 离坐标系原点的距离， θ 表示和水平轴的夹角。径向畸变可看成坐标点沿着长度方向发生了变化 δr, 也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化 δθ。)

畸变模型分为径向畸变和切向畸变，径向畸变如下：

切向畸变如下：

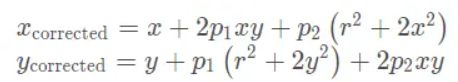组合上面两式，通过五个畸变系数找到空间点在像素平面上的正确位置：

1.将三维空间点P(X,Y,Z)投影到归一化图像平面。设它的归一化坐标为。

2.对归一化平面上的点进行径向畸变和切向畸变纠正

3.将纠正后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置

值得一提的是，存在两种去畸变处理（Undistort，或称畸变校正)做法。我们可以选择先对整张图像进行去畸变，得到去畸变后的图像，然后讨论此图像上的点的空间位置。或者，我们也可以先考虑图像中的某个点，然后按照去畸变方程，讨论它去畸变后的空间位置。二者都是可行的，不过前者在视觉 SLAM 中似乎更加常见一些。

如果把一张图像去畸变，写公式，流程

视差d与深度z的关系

在相机完成校正后，则有 z=fb/d,其中d表示视差，b表示基线，f是焦距，z是深度。这个公式其实很好记，在深度和焦距 f 确定的情况下，基线越大，视差也会越大。

图像处理

给一个二值图，求最大连通域

这个之后单独写一篇博客来研究这个好了，二值图的连通域应该是用基于图论的深度优先或者广度优先的方法，后来还接触过基于图的分割方法，采用的是并查集的数据结构，之后再作细致对比研究。

简单实现cv::Mat()

Mat是如何访问元素的？先访问行还是先访问列？

Mat访问像素一共有三种方法：使用at()方法、使用ptr()方法、使用迭代器、使用data指针

（1）使用at()方法：at()方法又是一个模板方法，所以在使用的时候需要传入图像像素的类型，例如：

（2）使用ptr()方法： ptr()方法能够返回指定行的地址（因此正常是先访问行的)，然后就可以移动指针访其他的像素。例如

这里需要注意的是，有时候在内存中会为了对齐而会对末尾的像素进行填充，而有时候没有填充。可以使用isContinue()来访问图像是否有填充，对于没有填充的图像，即连续的图像来说，遍历的时候就可以只要一层循环就可以了，他会自己换行将图像变成一维的来处理。

（3）使用迭代器：对Mat类型来说，他的迭代器类型可以使用MatIterator_或者Mat_::Iterator类型，具体使用如下

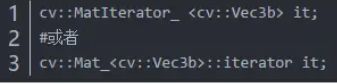用这两个迭代器便可以指定Mat对象的迭代器，注意需要传入模板参数。对迭代器的初始化与C++中的STL一致。

遍历也和前面指针一样，从图像左上角第一个像素开始遍历三个字节，然后第二个字节，依次遍历，到第一行遍历完后，就会到第二行来遍历。

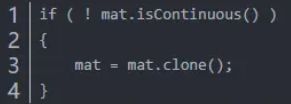
（4）使用data指针：用Mat存储一幅图像时，若图像在内存中是连续存储的（Mat对象的isContinuous == true），则可以将图像的数据看成是一个一维数组，而data（uchar*）成员就是指向图像数据的第一个字节的，因此可以用data指针访问图像的数据，从而加速Mat图像的访问速度。

一般经过裁剪的Mat图像，都不再连续了，如cv::Mat crop_img = src(rect);crop_img 是不连续的Mat图像，如果想转为连续的，最简单的方法，就是将不连续的crop_img 重新clone()一份给新的Mat就是连续的了，例如

李群&李代数

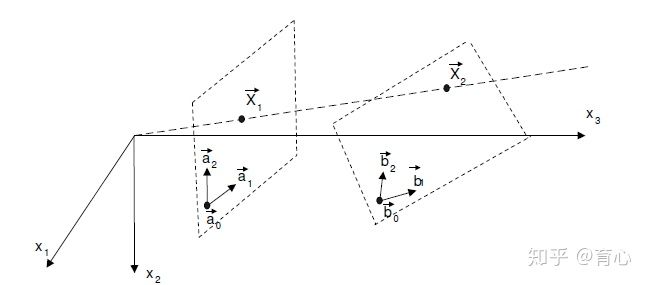
介绍一下李群和李代数的关系

解答：如上图所示(摘自《视觉SLAM十四讲》)，从李群到李代数是对数映射，形式上是先取对数，然后取∨，从李代数到李群是指数映射，形式上先取∧，再取指数，下面具体说：

三维旋转：李群就是三维旋转矩阵，李代数是三维轴角(长度代表旋转大小，方向代表旋转轴方向)，从李群到李代数是分别求轴角的角θ(通过矩阵的迹求反余弦)和向量a(旋转矩阵特征值1对应的特征向量)，从李代数到李群就是罗德罗杰斯公式。

三维变换：李群是四元变换矩阵，李代数是六维向量，从李群到李代数同样先求角和向量，然后需要求t，从李代数到李群的话通过上面的公式计算。

为什么要引入李群李代数

旋转矩阵自身是带有约束的，正交且行列式为1，他们作为优化变量时，会引入额外的约束，时优化变的困难，通过李群李代数的转换关系，把位姿估计变成无约束的优化问题。

单应矩阵&基础矩阵&本质矩阵

ORB-SLAM初始化的时候为什么要同时计算H矩阵和F矩阵？

简单地说，因为初始化的时候如果出现纯旋转或者所有特征点在同一个平面上的情况，F矩阵会发生自由度退化，而这个时候H矩阵会有较小误差，因此要同时计算H矩阵和F矩阵，那么这里补充两个问题：

• （1）ORB SLAM是怎样选用哪个矩阵去恢复旋转和平移的呢？

  评分 + 占比

• （2）F矩阵退化会发生在哪些情况下？

  F矩阵会在两种条件下发生退化，准确地说是三种，第一种是发生在仅旋转的情况下，第二种是发生在所有空间点共面的情况下，第三种是所有空间点和两个摄像机中心在一个二次曲面上，有可能发生退化（第三种情况暂时不予讨论，可参看《多视图几何》一书），下面我们来看下他们为什么会退化：参考上述链接

什么是Essential，Fundamental矩阵？

如何求解Ax=b的问题

参看我的另外一个总结博客多视图几何总结——基础矩阵、本质矩阵和单应矩阵的求解过程

计算H矩阵和F矩阵的时候有什么技巧呢？实际上在问归一化的操作

其中我能想到的技巧有两点，第一个是RANSAC操作，第二个是归一化操作，RANSAC操作前面已经解释过了，这里主要来分析下归一化操作，在《多视图几何》中提到了一种归一化八点法，方法是

• 先用归一化矩阵对图像坐标进行平移和尺度缩放，
• 然后利用八点法求解单应或者基础矩阵，
• 最后再利用归一化矩阵恢复真实的单应或者基础矩阵，

归一化具体操作如下：

具体操作：又称各项同性缩放（非同性缩放有额外开销，但是效果并未提升），步骤如下

• （1）对每幅图像中的坐标进行平移（每幅图像的平移不同）使点集的形心移至原点
• （2）对坐标系进行缩放使得点x=(x,y,w)中的x,y,w总体上有一样的平均值，注意，对坐标方向，选择的是各向同性，也就是说一个点的x和y坐标等量缩放
• （3）选择缩放因子使得点x到原点的平均距离等于

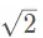
归一化具体操作优势如下：

• （1）提高了结果的精度；
• （2）归一化步骤通过为测量数据选择有效的标准坐标系，预先消除了坐标变换的影响，使得八点法对于相似变换不变。

单应矩阵H和基础矩阵F的区别是什么？

（1）基础矩阵F和单应矩阵H所求相机获取图像状态不同而选择不同的矩阵。

（2）本质矩阵E和基础矩阵F之间相差相机内参K的运算。

（3）只旋转不平移求出F并分解出的R，T和真实差距大不准确，能求H并分解得R。

Homography、Essential和Fundamental Matrix的区别

Homography Matrix可以将一个二维射影空间的2D点变换该另一个二维射影空间的2D点，如下图所示，在不加任何限制的情况下，仅仅考虑二维射影空间中的变换，一个单应矩阵H可由9个参数确定，减去scale的一个自由度，自由度为8。

Fundamental Matrix对两幅图像中任何一对2D对应点x和x′基础矩阵F都满足条件：

$x^T F x^{\prime}=0$，秩只有2，因此F的自由度为7。它自由度比本质矩阵多的原因是多了两个内参矩阵。

Essential matrix：本质矩是归一化图像坐标下的基本矩阵的特殊形式，其参数由运动的位姿决定，与相机内参无关，其自由度为6，考虑scale的话自由度为5。

参考多视图几何总结——基础矩阵、本质矩阵和单应矩阵的自由度分析

参考：三维重建笔记_相机标定(相机矩阵求解)基本概念汇总

单目相机，F和H矩阵有何不同，E和F矩阵有何不同，只旋转不平移能不能求F，只旋转不平移能不能求H

E=t^R

$F=K^{-T} E K^{-1}$

H=R-t*nT/d

在相机只有旋转而没有平移的情况，此时t为0，E也将为0，导致无法求解R，这时可以使用单应矩阵H求旋转，但仅有旋转，无法三角化求深度。

RANSAC && 鲁棒性检测

介绍RANSAC算法

RANSAC算法的基本假设是样本中包含正确数据(inliers，可以被模型描述的数据)，也包含异常数据(outliers，偏离正常范围很远、无法适应数学模型的数据)，即数据集中含有噪声。这些异常数据可能是由于错误的测量、错误的假设、错误的计算等产生的。同时RANSAC也假设，给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。

优缺点：

RANSAC算法的优点是能鲁棒的估计模型参数。例如，他能从包含大量局外点的数据集中估计出高精度的参数。缺点是它计算参数的迭代次数没有上限，如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到的可信的模型，概率与迭代次数成正比。另一个缺点是它要求设置跟问题相关的阈值，RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。

描述一下RANSAC算法

RANSAC算法是随机采样一致算法，从一组含有“外点”的数据中正确估计数学模型参数的迭代算法。“外点”一般指的是数据中的噪声，比如匹配中的误匹配和估计曲线中的离群点。因此，RANSAC算法是一种“外点”检测算法，也是一种不确定的算法，只能在一种概率下产生结果，并且这个概率会随着迭代次数的增加而加大。RANSAC主要解决样本中的外点问题，最多可以处理50%的外点情况。

RANSAC主要通过反复选择数据中的一组随机子集来达成目标，被选取的子集假设为局内点，验证步骤如下：

（1）一个模型适用于假设的局内点，也就是说所有的未知参数都能从假设的局内点计算得到。

（2）使用（1）中得到的模型测试所有其他数据，如果某个点适用于估计的模型，认为它也是局内点。

（3）如果有足够多的点被归类为假设的局内点，则估计的模型就足够合理。

（4）使用假设的局内点重新估计模型，因为它仅仅被初始的假设局内点估计。

（5）最终，通过估计局内点和模型的错误率估计模型。

RANSAC在选择最佳模型的时候用的metric是什么？

RANSAC在选择最佳模型的时候用的判断准则是什么?

最大一致集；

选择一致集时：简单地说一般是选用具有最小残差和的模型作为最佳模型。

除了RANSAC之外，还有什么鲁棒估计的方法？

解答：在《机器人的状态估计》一书中还介绍了M估计(广义的最大似然估计)和协方差估计，所谓M估计指的是加入鲁棒代价函数最大似然估计，而协方差估计指的是同时估计状态和协方差的方法，也称自适应估计。

（参考 计算机视觉中的数学方法 吴福朝 第17章）

M-估计

最小中值估计

位姿解算

特征点法

SIFT和SUFT的区别

共同点：

SIFT/SURF为了实现不同图像中相同场景的匹配，主要包括三个步骤：

1、尺度空间的建立；

2、特征点的提取；

3、利用特征点周围邻域的信息生成特征描述子

4、特征点匹配。

区别：

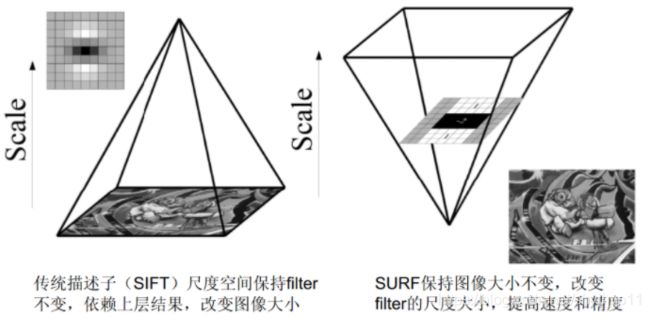
• 构建图像金字塔：SIFT特征利用不同尺寸的图像与相同的高斯差分滤波器卷积；SURF特征利用原图片与不同尺寸的方框滤波器卷积。

• 特征描述子：SIFT特征有4×4×8=128维描述子，SURF特征有4×4×4=64维描述子

• 特征描述子：SIFT特征有4×4×8=128维描述子，SURF特征有4×4×4=64维描述子

• 特征点检测方法：SIFT特征先进行非极大抑制，再去除低对比度的点，再通过Hessian矩阵去除边缘响应过大的点；SURF特征先利用Hessian矩阵确定候选点，然后进行非极大抑制

• 特征点主方向：SIFT特征在正方形区域内统计梯度幅值的直方图，直方图最大值对应主方向，可以有多个主方向；SURF特征在圆形区域内计算各个扇形范围内x、y方向的haar小波响应，模最大的扇形方向作为主方向

参考： 图像识别中SIFT算法与SURF算法的区别

• SIFT由David Lowe在1999年提出，在2004年加以完善 。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。SURF 算法，全称是 Speeded-Up Robust Features。该算子在保持 SIFT 算子优良性能特点的基础上，同时解决了 SIFT 计算复杂度高、耗时长的缺点，对兴趣点提取及其特征向量描述方面进行了改进，且计算速度得到提高。

什么是ORB特征，ORB特征的旋转不变性是如何做的，BRIEF算子是怎么提取的

ORB特征指的是Oriented FAST and rotated BREIF，包括改进后的FAST角点和BREIF特征子，ORB特征的旋转不变性主要是通过计算半径r范围内像素点的一阶矩，连接质心到特征点的向量作为主方向来对周围像素进行旋转，然后提取BRIEF特征子，BRIEF特征描述子通过计算出来的一个二进制串特征描述符来进行提取的。

在SLAM中，如何对匹配好的点做进一步的处理，更好保证匹配效果？

（1）确定匹配最大距离，汉明距离小于最小距离的两倍。

（2）使用KNN-matching算法，在这里设置K为2，每个匹配得到两个最接近的描述子，然后计算最接近距离和次接近距离之间的比值，当比值大于既定值时，才作为最终匹配。

（3）使用RANSAC算法找到最佳单应性矩阵，该函数使用的特征点同时包含正确和错误匹配点，因此计算的单应性矩阵依赖于二次投影的准确性。

ORB-SLAM中的特征是如何提取的？如何均匀化的？

ORB描述子的提取流程：

• 输入图像，并对输入图像进行预处理，将其转换成灰度图像；

• 初始化参数，包括特征点数量nfeatures，尺度scaleFactor，金字塔层数nlevel，初始阈值iniThFAST，最小阈值minThFAST等参数；

• 计算金字塔图像，使用8层金字塔，尺度因子为1.2，则通过对原图像进行不同层次的resize，可以获得8层金字塔的图像；

• 计算特征点：

  • 将图像分割成网格，每个网格大小为WxW=30x30像素；
  • 遍历每个网格；
  • 对每个网格提取FAST关键点，先用初始阈值iniThFAST提取，若提取不到关键点，则改用最小阈值minThFAST提取。（注意，初始阈值一般比最小阈值大）

• 对所有提取到的关键点利用

  八叉树的形式进行划分：

  • 按照像素宽和像素高的比值(网格数量）作为初始的节点数量，并将关键点坐标落在对应节点内的关键点分配入节点中；
  • 根据每个节点中存在的特征点数量作为判断依据，如果当前节点只有1个关键点，则停止分割。否则继续等分成4份；
  • 按照上述方法不断划分下去，如图所示，可见出现一个八叉树的结构，终止条件是节点的数目Lnode大于等于要求的特征点数量nfeatures；
  • 对满足条件的节点进行遍历，在每个节点中保存响应值最大的关键点，保证特征点的高性能；

• 对上述所保存的所有节点中的特征点计算主方向，利用灰度质心的方法计算主方向，上一讲中我们已经讲解过方法，这讲就不再赘述了；

• 对图像中每个关键点计算其描述子，值得注意的是，为了将主方向融入BRIEF中，在计算描述子时，ORB将pattern进行旋转，使得其具备旋转不变性；参考ORBSLAM2中ORB特征提取的特点。

特征匹配（稀疏）和稠密匹配区别

特征匹配：

（1）速度快，效率高，可以到亚像素级别，精度高

（2）匹配元素为物体的几何特征，对照明变化不敏感

稠密匹配

（1）速度慢，效率低

（2）对无纹理区域匹配效果不理想，对光强条件敏感

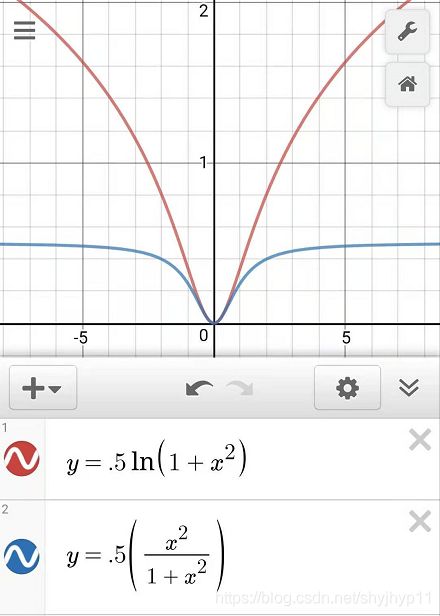
光流和直接法有何不同

光流仅估计了像素间的平移，但

（1）没有用相机结构

（2）没有考虑相机的旋转和图像缩放

（3）边界点追踪效果差

描述特征点法和直接法的优缺点

解答1

特征点法

优点：

（1）精确，直接法属于强假设

（2）运动过大时，只要匹配点在像素内，则不太会引起误匹配，鲁棒性好

缺点：

（1）关键点提取、描述子、匹配耗时长

（2）特征点丢失场景无法使用

（3）只能构建稀疏地图

直接法

优点：

（1）省去计算特征点、描述子时间

（2）可以用在特征缺失的场合（比如白墙）

（3）可以构建半稠密乃至稠密地图

缺点：

（1）易受光照和模糊影响

（2）运动必须微小，要求相机运动较慢或采样频率较高（可以用图像金字塔改善）

（3）非凸性；单个像素没有区分度

解答2

特征点法

优点：1. 没有直接法的强假设，更加精确；2. 相较与直接法，可以在更快的运动下工作，鲁棒性好

缺点：1. 特征提取和特征匹配过程耗时长；2. 特征点少的场景中无法使用；3.只能构建稀疏地图

直接法：

优点：1.省去了特征提取和特征匹配的时间，速度较快；2. 可以用在特征缺失的场合；3. 可以构建半稠密/稠密地图

缺点：1. 易受光照和模糊影响；2.运动必须慢；3.非凸性，易陷入局部极小解

描述PnP

解答1

Perspective-n-Points, PnP(P3P)提供了一种解决方案，它是一种由3D-2D的位姿求解方式，即需要已知匹配的3D点和图像2D点。目前遇到的场景主要有两个，其一是求解相机相对于某2维图像/3维物体的位姿；其二就是SLAM算法中估计相机位姿时通常需要PnP给出相机初始位姿。

在场景1中，我们通常输入的是物体在世界坐标系下的3D点以及这些3D点在图像上投影的2D点，因此求得的是相机坐标系相对于世界坐标系(Twc)的位姿

在场景2中，通常输入的是上一帧中的3D点（在上一帧的相机坐标系下表示的点）和这些3D点在当前帧中的投影得到的2D点，所以它求得的是当前帧相对于上一帧的位姿变换，如图所示：

两种情况本质上是相同的，都是基于已知3D点和对应的图像2D点求解相机运动的过程。

解答2

已知空间点世界坐标系3D坐标和其对应像素投影2D坐标，求当前相机坐标系，相对于世界坐标系的变换（R,t）。公式如下 $$ s\left(\begin{array}{c} u_1 \ v_1 \ 1 \end{array}\right)=\left(\begin{array}{llll} t_1 & t_2 & t_3 & t_4 \ t_5 & t_6 & t_7 & t_8 \ t_9 & t_{10} & t_{11} & t_{12} \end{array}\right)\left(\begin{array}{c} X \ Y \ Z \ 1 \end{array}\right) . $$ 目前一共有两种解法，直接线性变换方法（一对点能够构造两个线性约束，因此12个自由度一共需要6对匹配点），另外一种就是非线性优化的方法，假设空间坐标点准确，根据最小重投影误差优化相机位姿。

目前有两个主要场景场景，其一是求解相机相对于某2维图像/3维物体的位姿；其二就是SLAM算法中估计相机位姿时通常需要PnP给出相机初始位姿。

在场景1中，我们通常输入的是物体在世界坐标系下的3D点以及这些3D点在图像上投影的2D点，因此求得的是相机坐标系相对于世界坐标系(Twc)的位姿

在场景2中，通常输入的是上一帧中的3D点（在上一帧的相机坐标系下表示的点）和这些3D点在当前帧中的投影得到的2D点，所以它求得的是当前帧相对于上一帧的位姿变换

参考：三维重建笔记_相机标定(相机矩阵求解)基本概念汇总

ICP

ICP算法的原理是什么？简要叙述一下。

ICP算法的核心是最小化目标函数： $$ f(R, T)=\frac{1}{N_p} \sum_{i=1}^{N_p}\left|p_t^i-R \cdot p_s^i-T\right|^2 $$ 目标函数是指是对所有对应点之间的欧式距离的平方和。

给两组已经匹配好的3D点，计算相对位姿变换。已知匹配的ICP问题，写代码。

匹配两组已知坐标的3D点当然是采用ICP，参考《视觉SLAM十四讲》，ICP的解法一共有两种：SVD方法和非线性优化方法，下面过一遍SVD方法的推导过程： 参考：给两组已经匹配好的3D点，计算相对位姿变换，写代码

非线性优化计算位姿

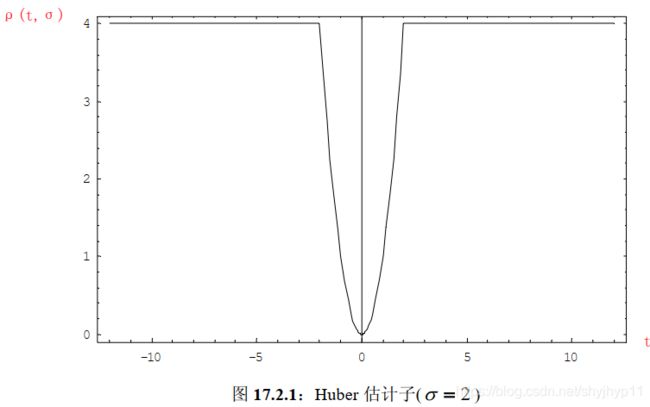
如果是利用非线性优化的方法获得位姿的话，可以在非线性优化代价函数中加入鲁棒核函数来减少无匹配所带来的误差，例如《视觉SLAM十四讲》里面提到的Huber核

在《机器人的状态估计》一书总将这种方法称为\M估计**，核函数还包裹Cauchy核

Geman-MeClure核

等等。

什么是极线约束

解答1

所谓极线约束就是说同一个点在两幅图像上的映射，已知左图映射点p1，那么右图映射点p2一定在相对于p1的极线上，这样可以减少待匹配的点数量。（画图解释）

解答2

所谓极线约束就是说同一个点在两幅图像上的映射，已知左图映射点p1，那么右图映射点p2一定在相对于p1的极线上，这样可以减少待匹配的点数量。如下图：

单目视觉slam中尺寸漂移是怎么产生的

解答1

单目相机根据一张图片无法得出一张图片中物体的实际大小，同理也就无法得出运动的尺度大小，这是产生尺度漂移的根源。而在优化过程中，单目相机使用对极几何中的三角测量原理，而三角测量中，极小的角度误差在累积之后深度不确定都会变得很大，从而无法保证尺度一致性。

解答2

用单目估计出来的位移，与真实世界相差一个比例，叫做尺度。这个比例在单目初始化时通过三角化确定，但单纯靠视觉无法确定这个比例到底有多大。由于SLAM过程中噪声的影响，这个比例还不是固定不变的。修正方式是通过回环检测计算Sim3进行修正。

后端优化

如何优化重投影误差？采用什么方法求解？如果误匹配的点重投影之后误差很大，如何解决它对整个优化问题的影响？

图优化模型，将路标点和相机位姿作为两个节点，观测模型作为边，同时优化两个变量

SLAM中常用L-M求解，如果误匹配误差很大可以考虑用核函数（Huber）

重投影误差的表达式，误差关于位姿的偏导数怎么算？误差关于空间点的偏导数怎么计算？

做图优化时，对比采用四元数法和李代数法在数学直观性、计算量上的差异性

画后端优化因子图

非线性优化

有哪几种鲁棒核函数？ 鲁棒核函数

总结：基本都是二次曲线或对数曲线的形式，加上取对数，加上分母项，加上权重项，加上分段的断点，来抑制过滤掉outlier.

除了 Huber 核之外，还有 Cauchy 核， Tukey 核等等（如上），读者可以看看 g2o 和 Ceres 都提供了哪些核函数。

梯度下降法、牛顿法、高斯-牛顿法的区别//hereto

在BA优化、PnP、直接法里面都有接触到非线性优化问题，上面几种方法都是针对对非线性优化问题提出的方法，将非线性最优化问题作如下展开，就可以获得梯度下降法和牛顿法 $$ |f(x+\Delta x)|_2^2 \approx|f(x)|_2^2+\boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}+\frac{1}{2} \Delta \boldsymbol{x}^T \boldsymbol{H} \Delta \boldsymbol{x} $$ 梯度下降法是一个一阶最优化算法，通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。因此指保留一阶梯度信息。缺点是过于贪心，容易走出锯齿路线。 $$ \Delta x^=-J^T(x) $$ 牛顿法是一个二阶最优化算法，基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似。因此保留二阶梯度信息。缺点是需要计算H矩阵，计算量太大。 $$ \Delta \boldsymbol{x}^=-\boldsymbol{J}^T(\boldsymbol{x}) / \boldsymbol{H} $$ 而把非线性问题，先进行一阶展开，然后再作平方处理就可以得到高斯-牛顿法和列文博格方法 $$ \begin{gathered} f(x+\Delta x) \approx f(x)+J(x) \Delta x . \ \Delta x^*=\arg \min _{\Delta x} \frac{1}{2}|f(x)+J(x) \Delta x|^2 . \end{gathered} $$ 高斯-牛顿法对上式展开并对Δx进行求导即可得高斯牛顿方程，其实其就是使用$\boldsymbol{J} \boldsymbol{J}^T$对牛顿法的H矩阵进行替换，但是$\boldsymbol{J} \boldsymbol{J}^T$有可能为奇异矩阵或变态，Δx也会造成结果不稳定，因此稳定性差$\boldsymbol{J}(\boldsymbol{x})^T \boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}=-\boldsymbol{J}(\boldsymbol{x})^T f(\boldsymbol{x})$

列文博格法就是在高斯-牛顿法的基础上对Δx添加一个信赖区域，保证其只在展开点附近有效，即其优化问题变为带有不等式约束的优化问题，利用Lagrange乘子求解 $$ \begin{gathered} \min _{\Delta \boldsymbol{x}_k} \frac{1}{2}\left|f\left(\boldsymbol{x}_k\right)+\boldsymbol{J}\left(\boldsymbol{x}_k\right) \Delta \boldsymbol{x}_k\right|^2+\frac{\lambda}{2}|\boldsymbol{D} \Delta \boldsymbol{x}|^2 . \ \left(\boldsymbol{H}+\lambda \boldsymbol{D}^T \boldsymbol{D}\right) \Delta \boldsymbol{x}=\boldsymbol{g} . \end{gathered} $$

介绍一下Gauss-Netwon和LM算法

描述下GN、LM方法

（1） GN：线搜索

将f（x）进行一节泰勒展开，最后求解

线性方程H△x=b；

用JT*J近似H矩阵，省略H复杂的计算

过程；

稳定性差，可能不收敛；

（2） LM：信赖区域；

求解线性方程(H+λI)△x=b；

提供更稳定，更准确的增量

一阶梯度下降，G-N和L-M三种方法的关系

(H+λI)△x=b

当λ= 0时，L-M等于G-N；

当λ= ∞时，L-M等于一阶梯度下降

L-M的好处就在于：如果下降的太快，使用较小的λ，如果下降的太慢，使用较大的λ

为什么SLAM中常用L-M

G-N中的H矩阵可能为奇异矩阵或者病态矩阵，导致算法不收敛。而且当步长较大时，也无法保证收敛性，所以采用L-M求解增量方程，但是它的收敛速度可能较慢。

LM算法里面那个 $\lambda$ 是如何变化的呢？

解答：这里我想从头开始理一遍，参考《视觉SLAM十四讲》首先LM算法优势在哪里，GN法采用雅克比矩阵的形式来代替难求的海森矩阵H，但是是半正定的，可能出现奇异矩阵或者病态的情况，而且Δx太大的时候也会导致这种二阶泰勒展开的近似不够准确，为解决第二个问题，提出了给Δx添加一个信赖区域方法，也就是LM法，其采用下式判断近似差异的大小，进而确定信赖区域范围：

其中分子是代价函数的\实际下降值**，分母是\近似下降值**。如果ρ越接近1说明近似越准确，ρ过小说明实际下降较小，需要缩小信赖区域范围，如果ρ过大说明实际下降较大，需要扩大信赖区域范围。其步骤如下：

• 初始化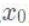和优化半径μ；
• 进行迭代求解

• 这里D为单位阵是信赖区域范围为一个球形；
• 计算ρ；
• 如果ρ>3/4，则μ=2μ(扩大信赖区域范围)；
• 如果ρ=1/4，则μ=0.5μ(缩小信赖区域范围)；
• 如果ρ大于某一阈值，则进行更新

• 这里面需要优化一个带约束的非线性优化函数，采用拉格朗日乘子法就引入了λ，如下

• 求解后获得

  

• 当D=I时有

  

• 求解后当λ较小时说明Δx近似于GN方法求解的结果，二阶是较好的近似，而λ较大时说明近似于一阶梯度下降法，二阶近似效果不够好。

说一下Dog-Leg算法

卡尔曼滤波

简述卡尔曼滤波

预测：如何从上一时刻的状态，根据输入信息推断当前时刻的状态分布（先验）

计算协方差

更新：计算增益Kg，然后计算后验

描述（扩展）卡尔曼滤波与粒子滤波，你自己在用卡尔曼滤波时遇到什么问题没有？

推导一下卡尔曼滤波、描述下粒子滤波

用自己的描述下，仅供参考

卡尔曼滤波：

卡尔曼滤波就是通过运动方程获得均值和方差的预测值，然后结合观测方程和预测的方差求得卡尔曼增益，然后在用卡尔曼增益更行均值和方差的预测值而获得估计值。

卡尔曼滤波推导的思路是（其中一种）先假定有这么一个修正公式 $$ \hat{x}_k=\hat{x}_k^{\prime}+K_k\left(z_k-\hat{z}_k\right)=\hat{x}_k^{\prime}+K_k\left(z_k-H \hat{x}_k^{\prime}\right) $$ 构真实值和估计值之间的协方差矩阵，然后通过对对角线元素求和获得方差表达式，我们的修正公式是需要使得方差最小，因此把方差表达式对$K_k$求导就可以获得卡尔曼增益的表达式，然后从先验到预测值的方差公式可以通过求预测值和真实值的协方差矩阵获得。

粒子滤波：

粒子滤波最常用的是SIR，其算法是用运动方程获得粒子的状态采样，然后用观测方程进行权值更新，通过新的粒子加权平均就获得新的估计状态，最后非常重要的一步就是重采用。

粒子滤波的推导中概念有很多，最重要的推导过程是重要性采样过程，其思路就是我原本的采样分布是不知道的，我如何从一个已知的分布中采样，通过加权的方式使得从已知的分布中采样的粒子分布和原本未知的分布中采样的粒子分布结果一致，从而引入SIS粒子滤波，再进一步加入重采样后就引入了SIR粒子滤波。

具体的可以参看我的另外两个总结博客

概率机器人总结——粒子滤波先实践再推导

概率机器人总结——(扩展)卡尔曼滤波先实践再推导

说明UKF，EKF和PF之间的关系

从精度的角度来看，所有高精度都是通过增加计算量来换来的，如果UKF通过加权减少Sigma点的方法来降低计算负载，那么精度在一定程度上会低于一阶泰勒展开的EKF线性化。除了EKF和UKF之间的时间复杂性问题外，我们还需要检查它们的理论性能。从以往的一些研究中中，我们知道UKF可以将状态估计和误差协方差预测到4阶精度，而EKF只能预测状态估计的2阶和误差协方差的4阶。但是，只有在状态误差分布中的峰度和高阶矩很明显的情况下，UKF才能进行更准确的估计。在我们的应用中，四元数分量协方差的大小显着小于统一性，这意味着峰度和更高阶矩非常小。这一事实说明了为什么UKF的性能不比EKF好。

另外，采样率也是另外一个拉小UKF与EKF差距的因素，对许多动态模型（有论文提到四元数动态）随着采样间隔的缩短，模型愈发趋近准线性化，那么越小的步长，积分步长把（四元数）传播到单位球面的偏差就越小。因此最小化了线性化误差。

最后，也是最根本的在选取EKF和UKF最直观的因素，UKF不用进行雅可比矩阵计算，但是，许多模型的求导是极为简单的，在最根本的地方UKF没有提供更优的解决方案。这也使得，状态模型的雅可比计算的简单性允许我们在计算EKF和UKF用相同的方法计算过程误差协方差。

UKF并不是万能的，也不是一定比EKF优秀，很多时候需要根据情况选择特定的滤波。

SLAM后端有滤波方法和非线性优化方法，这两种方法的优缺点是什么？

滤波方法的优点：在当前计算资源受限、待估计量比较简单的情况下，EKF为代表的滤波方法非常有效，经常用在激光SLAM中。

滤波方法的缺点：存储量和状态量是平方增长关系，因为存储的是协方差矩阵，因此不适合大型场景。但是现在视觉SLAM的方案中特征点的数据很大，滤波方法效率是很低的。

非线性优化方法一般以图优化为代表，在图优化中BA是核心，而包含大量特征点和相机位姿的BA计算量很大，无法实时。在后续的研究中，人们研究了SBA和硬件加速等先进方法，实现了实时的基于图优化的视觉SLAM方法。

BA优化

描述BA

BA的本质是一个优化模型，其目的是最小化重投影/光度误差，用于优化相机位姿和世界点。局部BA用于优化局部的相机位姿，提高跟踪的精确度；全局BA用于全局过程中的相机位姿，使相机经过长时间、长距离的移动之后，相机位姿还比较准确。BA是一个图优化模型，一般选择LM(Levenberg-Marquardt)算法并在此基础上利用BA模型的稀疏性进行计算；可以直接计算，也可以使用g2o或者Ceres等优化库进行计算。

Bundle Adjustment : 从视觉重建中提炼出最优的3D模型和相机参数（内参和外参），好似每一个特征点都会反射几束光线，当把相机位姿和特征点位置做出最优的调整后，这些光线都收束到相机相机光心。也就是根据相机的投影模型构造构造代价函数，利用非线性优化（比如高斯牛顿或列文伯格马夸而尔特）来求最优解，利用雅克比矩阵的稀疏性解增量方程，得到相机位姿和特征点3D位置的最优解。

BA可以分为基于滤波器的BA和基于迭代的BA

什么是BA优化

BA的全称是Bundle Adjustment优化，指的是从视觉重建中提炼出最优的三维模型和相机参数，包括内参和外参。从特征点反射出来的几束光线，在调整相机姿态和特征点空间位置后，最后收束到相机光心的过程。BA优化和冲投影的区别在于，对多段相机的位姿和位姿下的路标点的空间坐标进行优化。

将误差表示为： $$ e(\xi, p)=z-\frac{1}{s} K T P $$ 也就是： $$ e(\xi, p)=z-\frac{1}{s} K \cdot \exp \left(\xi^{\wedge}\right) \cdot P $$ 可以计算出误差对位姿和路标坐标的偏导： $$ \begin{gathered} J_{\delta \xi}=\frac{\partial \boldsymbol{e}}{\partial \delta \xi}=-\left[\begin{array}{cccccc} \frac{f_x}{Z^{\prime}} & 0 & -\frac{f_x X^{\prime}}{Z^{\prime 2}} & -\frac{f_x X^{\prime} Y^{\prime}}{Z^{\prime 2}} & f_x+\frac{f_x X^{\prime 2}}{Z^{\prime 2}} & -\frac{f_x Y^{\prime}}{Z^{\prime}} \ 0 & \frac{f_y}{Z^{\prime}} & -\frac{f_y Y^{\prime}}{Z^{\prime 2}} & -f_y-\frac{f_y Y^{\prime 2}}{Z^{\prime 2}} & \frac{f_y Y^{\prime} X^{\prime}}{Z^{\prime 2}} & \frac{f_y X^{\prime}}{Z^{\prime}} \end{array}\right] \ J_p=\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}}=-\left[\begin{array}{ccc} \frac{f_x}{Z^{\prime}} & 0 & -\frac{f_x X^{\prime}}{Z^{\prime 2}} \ 0 & \frac{f_y}{Z^{\prime}} & -\frac{f_y Y^{\prime}}{Z^{\prime 2}} \end{array}\right] \cdot \boldsymbol{R} \end{gathered} $$ 对于特征点位置p和m个位姿以及n个特征点，表示为： $$ \boldsymbol{x}=\left[\begin{array}{llll} \xi_1 & \xi_2 \ldots \xi_m \mid & p_1 & p_2 \ldots p_n \end{array}\right]^T $$ 上式中的右边简写为： $$ \begin{gathered} x_c=\left[\begin{array}{llll} \xi_1 & \xi_2 & \ldots & \xi_m \end{array}\right] \ x_p=\left[\begin{array}{llll} p_1 & p_2 & \ldots & p_n \end{array}\right] \end{gathered} $$ 然后，将优化的目标函数表示为： $$ \frac{1}{2}|f(x+\Delta x)|^2=\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^n\left|e_{i j}+F_{i j} \Delta \xi_i+E_{i j} \Delta p_j\right|^2 $$ 目标函数也可以表示为： $$ \frac{1}{2}|f(x+\Delta x)|^2=\frac{1}{2}\left|e+F \Delta x_c+E \Delta x_p\right|^2 $$ 对于线性增量方程： $$ H \Delta x=g $$ 这里的 $$ H=J^T J $$ 将雅克比矩阵分块为： $$ J=\left[\begin{array}{ll} F & E \end{array}\right], \quad J^T=\left[\begin{array}{l} F^T \ E^T \end{array}\right] $$ 则： $$ H=J^T J=\left[\begin{array}{ll} F^T F & F^T E \ E^T F & E^T E \end{array}\right] $$

给你m相机n个点的bundle adjustment。当我们在仿真的时候，在迭代的时候，相机的位姿会很快的接近真值。而地图点却不能很快的收敛这是为什么呢？

解答：约束相机位姿的方程远多于约束地图点的方程。

10个相机同时看到100个路标点，问BA优化的雅克比矩阵多少维

2000*360

因为误差对相机姿态的偏导数的维度是2×6,对路标点的偏导数是2×3，又10个相机可以同时看到100个路标点，所以一共有10×100×2行，100×3+10×6个块。 $$ J_{11}=\frac{\partial e_{11}}{\partial \boldsymbol{x}}=\left(\frac{\partial e_{11}}{\partial \boldsymbol{\xi}1}, \mathbf{0}{2 \times 6}, \frac{\partial e_{11}}{\partial p_1}, \mathbf{0}{2 \times 3}, \mathbf{0}{2 \times 3}, \mathbf{0}{2 \times 3}, \mathbf{0}{2 \times 3}, \mathbf{0}_{2 \times 3}\right) $$

关键帧的作用是什么

关键帧目前是一种非常常用的方法，可以减少待优化的帧数，并且可以代表其附近的帧。

如何选择关键帧？

选取关键帧的指标：

（1）距离上一关键帧的帧数是否足够多（时间）。运动很慢的时候，就会选择大量相似的关键帧，冗余、运动快的时候又丢失了很多重要的帧。

（2）距离最近关键帧的距离是否足够远（空间）运动。相邻帧根据姿态计算运动的相对大小，可以是位移，也可以是旋转，或者二者都考虑了。

（3）跟踪质量（主要根据跟踪过程中搜索到的点数和搜索的点数比例）/共视特征点。这种方法记录了当前视角下的特征点数或者视角，当相机离开当前场景时才会新建关键帧，避免了上一种方法存在的问题，缺点是比较复杂。

特征点法和直接法的BA有何不同

（1） 误差函数不同。特征点法是重投影误差，直接法是光度误差

（2） 雅克比矩阵不同

EKF和BA的区别

解答1

（1） EKF假设了马尔科夫性，认为k时刻的状态只与k-1时刻有关。非线性优化使用所有的历史数据，做全体的SLAM

（2） EKF做了线性化处理，在工作点处用一阶泰勒展开式近似整个函数，但在工作点较远处不一定成立。非线性优化每迭代一次，状态估计发生改变，我们会重新对新的估计点做 泰勒展开，可以把EKF看做只有一次迭代的BA

解答2

• （1） EKF假设了马尔科夫性，认为k时刻的状态只与k-1时刻有关。BA使用所有的历史数据，做全体的SLAM
• （2） EKF做了线性化处理，在工作点处用一阶泰勒展开式近似整个函数，但在工作点较远处不一定成立。BA每迭代一次，状态估计发生改变，我们会重新对新的估计点做泰勒展开，可以把EKF看做只有一次迭代的BA

工程实现

介绍下你熟悉的非线性优化库

非线性优化库一般有ceres和g2o两种，我比较熟悉的是g2o，看下g2o的结构图

它表示了g2o中的类结构。 首先根据前面的代码经验可以发现，我们最终使用的optimizer是一个SparseOptimizer对象，因此我们要维护的就是它(对它进行各种操作)。 一个SparseOptimizer是一个可优化图(OptimizableGraph)，也是一个超图(HyperGraph)。而图中有很多顶点(Vertex)和边(Edge)。顶点继承于BaseVertex，边继承于BaseUnaryEdge、BaseBinaryEdge或BaseMultiEdge。它们都是抽象的基类，实际有用的顶点和边都是它们的派生类。我们用SparseOptimizer.addVertex和SparseOptimizer.addEdge向一个图中添加顶点和边，最后调用SparseOptimizer.optimize完成优化。

在优化之前还需要制定求解器和迭代算法。一个SparseOptimizer拥有一个OptimizationAlgorithm，它继承自Gauss-Newton, Levernberg-Marquardt, Powell’s dogleg三者之一。同时，这个OptimizationAlgorithm拥有一个Solver，它含有两个部分。一个是 SparseBlockMatrix，用于计算稀疏的雅可比和海塞矩阵；一个是线性方程求解器，可从PCG、CSparse、Choldmod三选一，用于求解迭代过程中最关键的一步：$H \Delta x=-b$

因此理清了g2o的结构，也就知道了其使用流程。在之前已经说过了，这里就再重复一遍：

（1）选择一个线性方程求解器，PCG、CSparse、Choldmod三选一，来自g2o/solvers文件夹

（2）选择一个BlockSolver，用于求解雅克比和海塞矩阵，来自g2o/core文件夹

（3）选择一个迭代算法，GN、LM、DogLeg三选一，来自g2o/core文件夹

参考G2O图优化基础和SLAM的Bundle Adjustment(光束法平差)

这里我补充下：

注意到上面的结构图中，节点Basevertex，BaseBinaryEdge和BlockSolver<>等都是模板类，我们可以根据自己的需要初始化不同类型的节点和边以及求解器，以ORB SLAM2为例，分析下后端最典型的全局BA所用的边、节点和求解器：

（1）边是EdgeSE3ProjectXYZ，它其实就是继承自BaseBinaryEdge<2, Vector2d, VertexSBAPointXYZ, VertexSE3Expmap>，其模板类型里第一个参数是观测值维度，这里的观测值是其实就是我们的像素误差u,v u,vu,v，第二个参数就是我们观测值的类型，第三个第四个就是我们边两头节点的类型；

（2）相机节点VertexSE3Expmap，它其实就是继承自BaseVertex<6, SE3Quat>，其模板类第一个参数就是其维度，SE3是六维的这没毛病，第二个就是节点的类型，SE3Quat就是g2o自定义的SE3的类，类里面写了各种SE3的计算法则；

（3）空间点节点VertexSBAPointXYZ，它其实就是继承自BaseVertex<3, Vector3d>，其模板类第一个参数是说明咱空间点的维度是三维，第二个参数说明这个点的类型是Vector3d；

（4）求解器是BlockSolver_6_3，它其实就是BlockSolver< BlockSolverTraits<6, 3> >，6,3分别指代的就是边两边的维度了。

我记得我刚开始学习SLAM的时候自己想办法写后端的时候很纳闷这个图是怎么构建起来的，在ORB或者SVO里面，所有的地图点和关键帧都是以类的形式存在的，例如在ORB中是先将关键帧的节点添加起来，然后添加空间点，然后遍历空间点中记录的与哪些关键帧有关系，然后相应ID的关键帧的节点和空间点的节点连接起来，然后就把图建立起来了，我觉得不写类好像没有什么其他更好的办法了。

介绍一下Ceres优化库，比如你使用过里面哪些内容？

g2o工程化的注意事项

图优化流程：

①选择节点和边，确定参数化形式

②加入节点和边

③选择初值，开始迭代

④计算J和H

⑤解H△x = -b

⑥GN/LM

g2o需要实现其中的③-⑥

g2o

①选择线性方程求解器（PCG/Cspare/Choldmod）

②选择一个blockslover

③选择迭代方式（GN/LM/Dogleg）

实现过程 ：选择节点和边

节点：g2o :: VertexSE3Expmap（相机位姿）

g2o :: VertexSBApointXYZ（路标）

边：g2o :: EdgeProjectXYZ2UV（重投影误差）

优化求解过程中，g2o或者ceres的内部实现过程，有哪些加速计算的处理

回环检测 & 重定位

SLAM中的绑架问题是什么？

解答1

绑架问题就是重定位，指的是机器人缺少先前位置信息的情况下确定当前位姿。比如机器人在一个已经构建好地图的环境中，但它并不知道自己在地图中的相对位置，或者在移动过程中，由于传感器的暂时性功能故障或者相机的快速移动，导致先前的位置信息丢失，因此得重新确定机器人的位置。初始化绑架是一个通常状况的初始化问题，可以使用粒子滤波方法，重新分散例子到三维空间，被里程信息和随机扰动不断更新，初始化粒子收敛到可解释观察结果的区域。追踪丢失状态绑架，即在绑架发生之前，系统已经保存当前状态，则可以使用除视觉传感器之外的其他的传感器作为候补测量设备。

解答2

绑架问题就是重定位，是指机器人在缺少之前位置信息的情况下，如何去确定当前位姿。例如当机器人被安置在一个已经构建好地图的环境中，但是并不知道它在地图中的相对位置，或者在移动过程中，由于传感器的暂时性功能故障或相机的快速移动，都导致机器人先前的位置信息的丢失，在这种情况下如何重新确定自己的位置。

初始化绑架可以阐述为一种通常状况初始化问题，可使用蒙特卡洛估计器，即粒子滤波方法，重新分散粒子到三维位形空间里面，被里程信息和随机扰动不断更新，初始化粒子聚集到/收敛到可解释观察结果的区域。追踪丢失状态绑架，即在绑架发生之前，系统已经保存当前状态，则可以使用除视觉传感器之外的其他的传感器作为候补测量设备。

什么是回环检测？

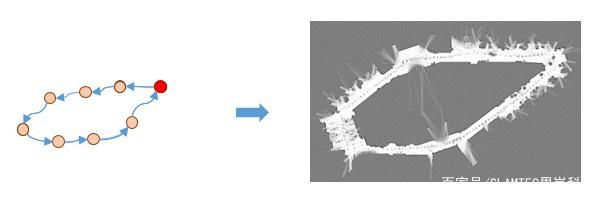
随着路径的不断延伸，机器人在建图过程中会存在一些累计误差，除了利用局部优化、全局优化等来调整之外，还可以利用回环检测来优化位姿。

什么是回环检测？

回环检测，又称闭环检测，是指机器人识别曾到达某场景，使得地图闭环的能力。说的简单点，就是机器人在左转一下，右转一下建图的时候能意识到某个地方是“我”曾经来过的，然后把此刻生成的地图与刚刚生成的地图做匹配。

　　

回环检测成功

回环检测之所以能成为一个难点，是因为：如果回环检测成功，可以显著地减小累积误差，帮助机器人更精准、快速的进行避障导航工作。而错误的检测结果可能使地图变得很糟糕。因此，回环检测在大面积、大场景地图构建上是非常有必要的 。

　

回环检测失败

如何提升机器人回环检测能力？

那么，怎么才能让机器人的回环检测能力得到一个质的提升呢？首先要有一个算法上的优化。

基于图优化的SLAM算法

基于图优化的SLAM 3.0 算是提升机器人回环检测能力的一大突破。

SLAM 3.0采用图优化的方式进行建图，进行了图片集成与优化处理，当机器人运动到已经探索过的原环境时，SLAM 3.0可依赖内部的拓扑图进行主动式的闭环检测。当发现了新的闭环信息后，SLAM 3.0使用Bundle Adjuestment(BA)等算法对原先的位姿拓扑地图进行修正（即进行图优化），从而能有效的进行闭环后地图的修正，实现更加可靠的环境建图。

SLAM 3.0闭环检测

SLAM 3.0环路闭合逻辑：先小闭环，后大闭环 ；选择特征丰富的点作为闭环点；多走重合之路，完善闭环细节。即使在超大场景下建图，也不慌。

超大场景下建图完整闭合过程

词袋模型

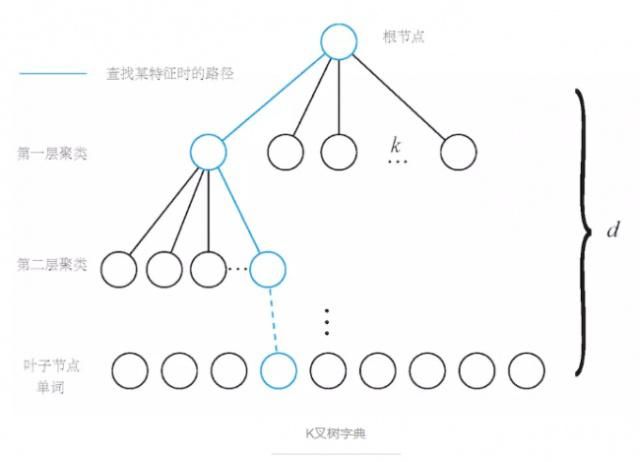
除了SLAM算法的升级和优化之外，现在还有很多系统采用成熟的词袋模型方法来帮助机器人完成闭环，说的简单点就是把帧与帧之间进行特征比配。

1、从每幅图像中提取特征点和特征描述，特征描述一般是一个多维向量，因此可以计算两个特征描述之间的距离；

2、将这些特征描述进行聚类（比如k－means），类别的个数就是词典的单词数，比如1000；也可以用Beyes、SVM等；

3、将这些词典组织成树的形式，方便搜索。

利用这个树，就可以将时间复杂度降低到对数级别，大大加速了特征匹配。

相似度计算

这种做法是从外观上根据两幅图像的相似性确定回环检测关系，那么，如何确定两个地图之间的相关性呢？

比如对于图像A和图像B，我们要计算它们之间的相似性评分：s(A,B)。如果单单用两幅图像相减然后取范数，即为： s(A,B)=||AB||s(A,B)=||AB||。但是由于一幅图像在不同角度或者不同光线下其结果会相差很多，所以不使用这个函数。而是使用相似度计算公式。

这里，我们提供一种方法叫TF-IDF。

TF的意思是：某特征在一幅图像中经常出现，它的区分度就越高。另一方面，IDF的思想是，某特征在字典中出现的频率越低，则分类图像时的区分度越高。

对于IDF部分，假设所有特征数量为n，某个节点的Wi所含的数量特征为Ni，那么该单词的IDF为：

TF是指某个特征在单副图像中出现的频率。假设图像A中单词Wi出现了N次，而一共出现的单词次数是n，那么TF为：

于是Wi的权重等于TF乘IDF之积，即：

考虑权重以后，对于某副图像，我们可以得到许多个单词，得到BOW：

（A表示某幅地图）

如何计算俩副图像相似度，这里使用了L1范数形式：

深度学习及其他

除了上面的几种方式之外，回环检测也可以建成一个模型识别问题，利用深度学习的方法帮助机器人完成回环检测。比如：决策树、SVM等。

……

最后，当回环出现以后，也不要急着就让机器人停止运动，要继续保持运动，多走重合的路，在已经完成闭合的路径上，进一步扫图完善细节。

　

继续走重合之路，完善闭环细节

所以，回环检测在SLAM中的作用也很重要哦。

参考资料

• SLAM大法之回环检测

重定位和回环检测的区别是什么？

重定位是跟丢以后重新找回当前的姿态，通过当前帧和关键帧之间的特征匹配，定位当前帧的相机位姿。重定位就是重新定位，当前图像因为和最近的图像或者局部地图之间缺乏足够的匹配，导致机器人无法确定自己的位姿，此时处于当前状态的机器人不再知道其在地图中的位置，也叫做机器人被“绑架”，就说的是人质被蒙上双眼带到未知地方，蒙罩去掉后完全不知道自己在哪里，这时候就需要充分利用之前建好的地图或者存好的数据库。此时机器人需要观察周围环境，并且从已有地图中寻找可靠的匹配关系，一般是关键帧信息，这样就可以根据已有信息“重新”估计机器人的姿态。

回环检测是为了解决位置估计随时间漂移的问题。主要是通过识别曾经到过的场景，将其与当前帧对应，优化整个地图信息，包括3D路标点、相机位姿和相对尺度信息。回环的主要目的是降低机器人随时间增加，轨迹中累积的漂移，一般发生在建图过程中。这是因为基于运动传感器或者视觉信息的里程计容易出错，使估计的轨迹偏离其实际真实的情况。通过回环，优化整个地图信息，包括3D路标点、相机位姿和相对尺度信息。回环检测提供了回环帧与所有历史帧的关系，可以极大减少误差。回环主要是纠正机器人/相机轨迹，而重新定位再从未知状态找回姿态。两者都需要当前图像预先访问过之前的位置附近，本质上都是一个图像识别问题。

重定位和回环检测的区别：

重定位主要为了恢复姿态估计，而回环是为了解决漂移，提高全局精度。二者容易混淆的原因是重定位通常也需要找到与之前帧的对应关系求解出姿态，而这可以通过回环来完成，很多算法是可以共享的。

常用的回环检测方法有哪些 / 闭环检测常用方法

ORB SLAM中采用的是词袋模型进行闭环检测筛选出候选帧，再通过求解判断最合适的关键帧

• Sim3：使用3对匹配点来进行相似变换（similarity transformation）的求解，进而解出两个坐标系之间的旋转矩阵、平移向量和尺度

LSD SLAM中的闭环检测主要是根据视差、关键帧连接关系，找出候选帧，然后对每个候选帧和测试的关键帧之间进行双向Sim3跟踪，如果求解出的两个李代数满足马氏距离在一定范围内，则认为是闭环成功

建图

说一下3D空间的位姿如何去表达?

解答：李群或者李代数。

给一组点云，从中提取平面

点云配准算法目前有哪些？

点云配准算法目前有ICP、KC、RPM、形状描述符配准和UPF/UKF。

（1）ICP

ICP算法简单且计算复杂度度低，使它成为最受欢迎的刚性点云配准方法。ICP算法以最近距离标准为基础迭代地分配对应关系，并且获得关于两个点云的刚性变换最小二乘。然后重新决定对应关系并继续迭代知道到达最小值。目前有很多点云配追算法都是基于ICP的改进或者变形，主要改进了点云选择、配准到最小控制策略算法的各个阶段。ICP算法虽然因为简单而被广泛应用。但是它易于陷入局部最大值。ICP算法严重依赖初始配准位置，它要求两个点云的初始位置必须足够近，并且当存在噪声点、外点时可能导致配准失败。

（2）KC

KC算法应用了稳健统计和测量方法。Tsin和Kanade应用核密度估计，将点云表示成概率密度，提出了核心相关（Kernel Correlation，简称KC）算法。这种计算最优配准的方法通过设置两个点云间的相似度测量来减小它们的距离。对全局目标函数执行最优化算法，使目标函数值减小到收敛域。因为一个点云中的点必须和另一个点云中的所有点进行比较，所以这种方法的算法复杂度很高。

（3）RPM

为了克服ICP算法对初始位置的局限性，基于概率论的方法被研究出来。Gold提出了鲁棒点匹配（Robust Point Matching，简称RPM）算法，以及其改进算法。这种方法应用了退货算法减小穷举搜索时间。RPM算法既可以用于刚性配准，也可以用于非刚性配准。对于RPM算法，在存在噪声点或者某些结构缺失时，配准可能失败。

（4）形状描述符配准

形状描述符配准在初始位置很差的情况下也能大体上很好的实现配准。它配准的前提是假设了一个点云密度，在没有这个特殊假设的情况下，如果将一个系数的点云匹配到一个稠密的点云，这种匹配方法将失败。

（5）UPF/UKF

尽管UPF算法能够精确的配准较小的数据集，但是它需要大量的粒子来实现精确配准。由于存在巨大的计算复杂度，这种方法不能用于大型点云数据的配准。为了解决这个问题，UKF算法被提出来，这种方法收到了状态向量是单峰假设的限制，因此，对于多峰分布的情况，这种方法会配准失败。

地图点的构建方法有哪些？

（1）在ORB SLAM2中是根据三角化的方法确定地图点的，利用匹配好的图像点对, 构建AX=b的方程，然后利用SVD分解取最小奇异值对应的特征向量作为地图点坐标，参考多视图几何总结——三角形法

（2）在SVO中是利用深度滤波器进行种子点深度更新，当种子点深度收敛后就加入地图构建地图点。

（在LSD中好像没有维护地图点，不断维护的是关键帧上的深度图）

ORB-SLAM3中的求3D点的算法流程(初始化过程)

输入: 一对图像的多组2D点对;

输出: 这两帧图像的相对运动(相对位姿: R,t)及D对应的3D点坐标

• 8点法求解基础矩阵F

• 根据内参求本质矩阵E ( E21 = K.t()* F21 * K ; )

• 对本质矩阵E()进行SVD分解, 分解出两幅图像的相对运动R,t(四组解)

• 构造摄像机矩P=K[R,t], 根据等式x = PX (x图像点坐标,X待求的三维点), 进行三角化(Triangulate),求出3D点坐标, 根据z值的正负,剔除异常点和不符合要求的R,t; 至此根据多组图像2D点对, 得到了位姿和对应的3D点(地图点)坐标.

• 三角化: 列方程Ax = 0 (即)；SVD分解， 则A=U W V^T中， V的第三列即为3D点坐标。

  void TwoViewReconstruction::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
  {
      cv::Mat A(4,4,CV_32F);
  
      A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
      A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
      A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
      A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
  
      cv::Mat u,w,vt;
      cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
      x3D = vt.row(3).t();
      x3D = x3D.rowRange(0,3)/x3D.at(3);
  }

如果对于一个3D点，我们在连续帧之间形成了2D特征点之间的匹配，但是这个匹配中可能存在错误的匹配。请问你如何去构建3D点？

毋庸置疑首先想到的是用\RANSAC方法**进行连续帧之间的位姿估计，然后用内点三角化恢复地图点，具体一点说使用RANSAC估计基础矩阵的算法步骤如下：

基本矩阵F的自动估计

（参考 计算机视觉中的数学方法 吴福朝 17.1.3节）

RANSAC 方法可以从有误匹配的点对应集中估计基本矩阵，这使得从两幅图像自动估计基本矩阵成为可能。基本矩阵自动估计的步骤如下：

• 自动提取两幅图像的特征点集并建立初始“匹配对集” ；

• RANSAC 去除错误匹配对：

  • 计算当前抽样所确定的基本矩阵 F，和它的一致点集 S(F)；
  • 如果当前的一致集大于原先的一致集， 则保持当前的一致集 S(F)和相应的基本矩阵 F，并删去原先的一致集和相应的基本矩阵；
  • 由自适应算法终止抽样过程，获得\最大一致集**，最大一致集中的匹配对(内点)是正确匹配对。

• 由最大一致集(即正确匹配对)重新估计基本矩阵。

为了自动估计基本矩阵，首先需要从两幅图像自动建立一个“点对应集”，可以容忍这个点对应集包含有大量的误匹配，因为在 RANSAC 估计方法中，理论上只要存在 8 个“好”的点对应就可以估计出基本矩阵。

3D地图点是怎么存储的？表达方式？

解答：以ORB SLAM2为例，3D地图点是以类的形式存储的，在类里面除了

• 存储3D地图点的空间坐标，
• 同时还存储了3D点对应的（多个）图像点的描述子(其实就是BRIFE描述子)，用来快速进行与特征点的匹配，
• 同时还用一个map存储了与其有观测关系的关键帧以及其在关键帧中的Index等等。

class MapPoint
{

// ...

protected:   
     // Position in absolute coordinates
     cv::Mat mWorldPos;

     // Keyframes observing the point and associated index in keyframe
     std::map > mObservations;
     // For save relation without pointer, this is necessary for save/load function
     std::map mBackupObservationsId1;
     std::map mBackupObservationsId2;

     // Mean viewing direction
     cv::Mat mNormalVector;

     // Best descriptor to fast matching
     cv::Mat mDescriptor;

     // Reference KeyFrame
     KeyFrame* mpRefKF;
     long unsigned int mBackupRefKFId;

     // Tracking counters
     int mnVisible;
     int mnFound;

     // Bad flag (we do not currently erase MapPoint from memory)
     bool mbBad;
     MapPoint* mpReplaced;
     // For save relation without pointer, this is necessary for save/load function
     long long int mBackupReplacedId;

     // Scale invariance distances
     float mfMinDistance;
     float mfMaxDistance;

     Map* mpMap;

     std::mutex mMutexPos;
     std::mutex mMutexFeatures;
     std::mutex mMutexMap;
};

多传感器

除了视觉传感，还用过其他传感吗？比如GPS，激光雷达

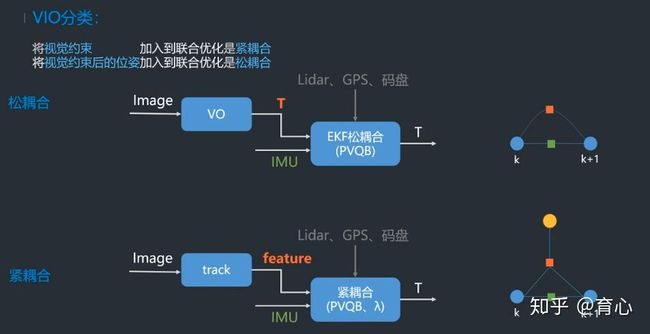
什么是紧耦合、松耦合？优缺点

这里默认指的是VIO中的松紧耦合，这里参考深蓝学院的公开课里面介绍：

紧耦合是把图像的特征加到特征向量中去，这样做优点是可以免去中间状态的累计误差，提高精度，缺点是系统状态向量的维数会非常高，需要很高的计算量；

松耦合是把VO处理后获得的变换矩阵和IMU进行融合，这样做优点是计算量小但是会带来累计误差。

下面是对经典的VIO框架进行一个分类

安装2D lidar的平台匀速旋转的时候，去激光数据畸变，写代码

在给定一些有噪声的GPS信号的时候如何去精准的定位？

如何标定IMU与相机之间的外参数？

目前我还没有实际标定过，标定方法可以参考贺一家博士的博客Kalibr 标定双目内外参数以及 IMU 外参数，像Intel出的D435i是已经标定号外参数的，另外在VINS-mono中可以对相机的外参数进行估计

给你xx误差的GPS，给你xx误差的惯导你怎么得到一个cm级别的地图？

在视觉SLAM中可能用到有关的边缘检测算子有哪些？

解答1

在边缘检测一般分为滤波、增强和检测三个步骤，其基本原理是用高斯滤波器进行去噪，之后再用卷积内核寻找像素梯度。边缘检测算子：

（1）canny算子：一种完善的边缘检测算法，抗噪能力强，用高斯滤波平滑图像，用一阶偏导的有限差分计算梯度的幅值和方向，对梯度幅值进行非极大值抑制，采用双阈值检测和连接边缘。

（2）sobel算子：一阶导数算子，引入局部平均运算，对噪声具有平滑作用，抗噪声能力强，计算量较大，但定位精度不高，得到的边缘比较粗，适用于精度要求不高的场合。

（3）laplacian算子：二阶微分算子，具有旋转不变性，容易受噪声影响，不能检测边缘的方向，一般不直接用于检测边缘，而是判断明暗变化。

解答2

• 边缘检测一般分为三步，分别是滤波、增强、检测。基本原理都是用高斯滤波器进行去噪，之后在用卷积内核寻找像素梯度。常用有三种算法：canny算子，sobel算子，laplacian算子
• canny算子：一种完善的边缘检测算法，抗噪能力强，用高斯滤波平滑图像，用一阶偏导的有限差分计算梯度的幅值和方向，对梯度幅值进行非极大值抑制，采用双阈值检测和连接边缘。
• sobel算子：一阶导数算子，引入局部平均运算，对噪声具有平滑作用，抗噪声能力强，计算量较大，但定位精度不高，得到的边缘比较粗，适用于精度要求不高的场合。
• laplacian算子：二阶微分算子，具有旋转不变性，容易受噪声影响，不能检测边缘的方向，一般不直接用于检测边缘，而是判断明暗变化。

什么是边缘化？First Estimate Jacobian？一致性？可观性？

边缘化的过程全面分析，示意图，公式推导，优缺点，哪些矩阵块有改变

时间戳对齐

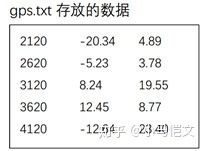
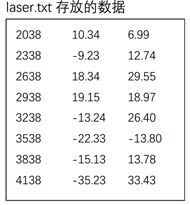
工程目录下有GPS保存的坐标文件gps.txt和激光雷达保存的坐标文件laser.txt两个文件，两个文件的第一列为记录当前数据的时间戳，后两列为坐标。由于GPS每隔500时间单位保存一次数据，激光雷达每隔300时间单位保存一次数据，因此，一段时间内激光雷达保存的数据比GPS保存的数据要多。现在想取出两个文件中时间戳最接近的数据，并分别存放在gps2.txt和laser2.txt中，编写程序实现。（不知道哪位大神能讲下这道题。。。）

ROS系统

ROS中rosrun和roslaunch的区别是什么

rosrun允许在任意软件包中运行可执行文件，而无需先在其中进行cd或roscd。

Roslaunch可以通过ssh在本地和远程轻松启动多个ros节点，以及在参数服务器上设置参数。它包括自动重生已经死掉的进程的选项。roslaunch接收一个或多个XML配置文件，这些文件指定要设置的参数和要启动的节点以及应在其上运行的计算机。

rosrun只能运行一个节点，如果要运行多个节点，就需要多次使用rosrun命令，而roslaunch可以采用xml格式描述运行的节点，同时运行多个节点。

开源SLAM算法

介绍经典的视觉SLAM框架

视觉SLAM总结——ORB SLAM2中关键知识点总结

视觉SLAM总结——SVO中关键知识点总结

视觉SLAM总结——LSD SLAM中关键知识点总结

说一个自己熟悉的SLAM算法，Lidar/Visual slam，说优缺点

读Maplab，设计室内服务机器人地图更新的方法、流程

说一下VINS-Mono的优缺点

AprilTag

Apriltag原理简介及源代码

Apriltag原理简介及源代码

CSDN首页 博客 下载 学习 社区 GitCode 云服务 猿如意 空间定位 搜索

会员中心 足迹 动态 消息 创作中心 发布 Apriltag原理简介及源代码

躺着中枪ing

于 2019-05-16 13:41:05 发布

38311 收藏 255 分类专栏： 机器视觉 apriltag 视觉定位 文章标签： 机器视觉 apriltag 空间定位 版权

机器视觉 同时被 3 个专栏收录 3 篇文章0 订阅 订阅专栏

apriltag 1 篇文章0 订阅 订阅专栏

视觉定位 1 篇文章0 订阅 订阅专栏 概要 AprilTag视觉定位Python实现 AprilTag过程 AprilTag边缘检测 四边形检测 编码与解码 实现代码 AprilTag视觉定位Python实现 AprilTag是一个视觉基准库，在AR，机器人，相机校准领域广泛使用。通过特定的标志（与二维码相似，但是降低了复杂度以满足实时性要求），可以快速地检测标志，并计算相对位置。 官网：https://april.eecs.umich.edu/software/apriltag.htmlAprilTag示例

AprilTag过程 AprilTag内容主要包含三个步骤。

第一步是如何根据梯度检测出图像中的各种边缘。 第二步即如何在边缘图像中找出需要的四边形图案并进行筛选，AprilTag尽可能的对检测出的边缘检测，首先剔除非直线边缘，在直线边缘进行邻接边缘查找，最终若形成闭环则为检测到一个四边形。 最后一个步便是如何进行二维码编码和二维码解码，编码方式分为三种，其黑边色块长度分别为8，7，6三个色块长度，对于解码内容，要在检测到的四边形内生成点阵列用于计算每色块的值，再根据局部二值模式(Local Binary Patterns)构造简单分类器对四边形内的色块进行分类，将正例色块编码为1将负例色块编码为0，就可以得到该二维码的编码。得到编码以后再与已知库内的编码进行匹配，确定解码出的二维码是否为正确。 AprilTag边缘检测 对于第一步来说，最主要的功能就是寻找图像中的边缘，原文章使用的是局部二值模式，但是实际使用中，我建议可以使用Canny算子方法，虽然检测出的边缘会减少，但是相应的也降低了图像中的噪点。局部二值 canny算子

四边形检测 对于得到的二值化边缘图像，需要对其进行多边形分析，首先运用 边缘结构分析(Topological structural analysis of digitized binary images)查找多边形，该方法用于确定二值图像边缘的围绕关系，即确定外边缘，内边缘以及它们之间嵌套关系，确定的边缘都与原图都有相对应的关系，因此完全可以用边缘来表示原图。该算法采用编码的思想，首先赋予不同的边缘以不同的编码值，这样方便确认多边形的层次关系。算法从起点开始，编辑边缘的像素，寻找该起始点同类的边缘点，当扫描至起始点时，该多边形闭环形成，切换至下一个起始点重复该操作，直到所有的二值点都被遍历，排除边数小于4的，将满足条件的进行进一步处理。

利用多边形凸包寻找算法(Finding the convex hull of a simple polygon)，计算每一个多边形本身的凸包，并求凸包及其多边形的面积，将两个面积进行比较，当多边形面积比凸包大时将该多边形排除，这样子可以有效的排除非凸多边形，以及不满足多边形面积与凸包面积之比大于0.8的多边形，保留满足条件的其余多边形。 多边形检测 对于最终满足条件的多边形，使用道格拉斯-普克算法(Douglas-Peucker algorithm)进行四边形逼近。

1 寻找曲线的两个端点A，B，作曲线间的弦即线段AB。

2 求线段AB到曲线上的距离最远的点C，并求其间的距离d。

3 将该距离d与提前设定的阈值进行比较，如果小于阈值，就可直接将该直线近似为曲线，该段曲线处理完毕。

4 如果距离d大于给定的阈值，用点C将曲线分割成为AC与BC，并分别对两段取线进行1至3的处理。

5 当所有曲线都处理完毕时，依次连接各个分割点形成的折线，这样就可将处理前的曲线近似成为直线，排除该情况下顶点数不为4的多边形。 1 2 3 4 5 6 7 8 9 检测出的四边形 图中表示的就是经过筛选后得到四边形的整个过程。查找四边形过程

编码与解码 在上一步检测出的四边形并不一定满足我们的要求，所以需要对上一步得到的四边形进行编码，匹配，检查。对于得到的四边形，首先要确定其内部的点阵，上一步的四边形是以四个顶点的形式进行存储的，根据这四个点可以确定其四边形内的点阵的具体坐标，不同编码方式其点阵的个数不相同(根据选择编码方式不同有8 ∗ 8 , 7 ∗ 7 , 6 ∗ 6 88,77,668∗8,7∗7,6∗6可选)，其编码方式由使用者对物体进行标定时确定，根据编码方式的不同，生成不同的内点坐标。以图???所示举例，该二维码的边长为6个黑边，其中的有效编码区域是除去外部黑边的4 ∗ 4 444∗4的部分，该部分区域有黑有白，用于二维码的编码。 图片点阵 具体的编码方式如下：

在这里插入图片描述

在确定的四边形中明确点阵坐标，在灰度图像中提取点阵的最外围一圈的像素的平均值Value1，再提取点阵次外外围一圈的像素的平均值Value2，根据AprilTag本身的二维码库的设计，四边形最外一层的虽有点的灰度值都是黑色的，而此外层的灰度值是黑色与白色混合，因此在同一光照环境下，Value1和Value2有明显的阈值分界线，确定阈值为Value1与Value2的均值，重新遍历整个点阵所有点坐标的像素值高于阈值的部分编码为0，低于阈值的部分编码为1，见图???。如此以来，从第一行开始进行编码，直至整个点阵被编码完成，将编码排列起来会得到一串二进制码，该二进制码的长度由具体的编码方式决定（分为36，25，16三种），每个四边形都能得到一串二进制码，该码表示该状态下二维码的编码，错误的四边形往往会生成错误的编码，错误编码无法在阈值范围内匹配到相应的ID，故可以轻松的排除错误编码的四边形，对得到的四边形进行编码并进行匹配校验是重要的一个过程。

进一步确定编码是否可靠，要与已知的编码库进行匹配，由于观察到的编码存在旋转的情况，所以应先将得到的编码进行三次90°旋转共得到四个方向上的编码，再逐一与编码库进行比较，求解编码之间的汉明距离(Hamming Distance，汉明距离是表示两个二进制编码之间的相似程度的一种距离，汉明距离是两个长二进制串之间位数不相同的个数。当观察编码与已知库里的某一编码的汉明距离小于给定的阈值时(一般为2)，就确定该观察编码的ID为与之匹配的编码库里的ID，并记录下该汉明距离，若编码库并没有一个与之匹配就确定该观察编码有误，则舍弃该编码对应的四边形。

经过上述的筛选与验证，至此观察编码的ID以及编码的旋转已经可以确定，便可计算该二维码的其他参数，包括二维码相对于原二维码的旋转方位，观察二维码与匹配二维码的相似程度，其中主要为二维码的单线性变换矩阵(Homography Matrix)}，在计算机领域中的针孔相机模型下，同一个张图形在不同空间内都有相关性，单线性变换就是将这个图片在该空间下映射至另一个与之对应的空间下，单线性变化矩阵就是这种映射矩阵且可分解出寻转矩阵与平移矩阵，根据上一个步骤求出的四个顶点的坐标即可求出相对于原始坐标的单线性变换矩阵，利用单线性变换矩阵结合多相机的信息，可以得到二维码的相关姿势信息。分解该矩阵就可求出旋转变换向量rvec以及平移变换向量tvec，对于得到的旋转向量，可以根据该向量求得二维码的正确姿势。

实现代码 这个算法是一个开源算法。 原始C代码地址为:https://april.eecs.umich.edu/software/apriltag 我个人将它重构为C#代码：https://github.com/BlackJocker1995/Apriltagcsharp python代码：https://github.com/BlackJocker1995/Apriltag_python

躺着中枪ing 关注

32

255 打赏

34

专栏目录 aprilslam, ROS下AprilTags的映射和姿态估计.zip 09-18 aprilslam, ROS下AprilTags的映射和姿态估计 AprilSLAM - AprilTags的映射和本地化AprilSLAM是一个用于在非结构化环境中从单个或者多个 AprilTags(link) 快速进行相机姿态。 AprilSLAM不需要预先知道标签的位置来估计相机的姿态。 只要在 AprilTags图像识别定位实例 qq_42238850的博客 1万+ 引言 AprilTags图像识别与定位 AprilTags是密歇根大学Edwin Olson教授及其实验室团队在2011年率先提出的一种标记识别算法，目前程序包已经开源，并且广泛运用到机器人和无人机的视觉导航当中。那么本文主要是以AprilTags程序包为基础，为大家做一个关于无人机实时位姿测定的实例演示。 准备工具 为了能够更方便地在自己的电脑上（以Win10为例）运行AprilTags实例，建... 评论34条写评论 KIKU啊 热评 您好，我使用您的Python代码，发现，它不具备旋转不变性，可以检测出4个角点，但无法分辨tag码的正反方向。 AprilTag简介与简单实用(自用资料整理)_whf7890的博客... 10-6 AprilTag是由University of Michigan的APRIL Robotics Laboratory提出的,官网是这里。官方自己对AprilTag的描述是视觉基准系统(Visual Fiducial System),其应用领域包括AR、机器人、相机校正等。通过对AprilTag Marker的识别,可以确定相机的位姿(... AprilTag_ros的使用_manbushuizhong的博客_apriltag ros 10-10 gitclonehttps://github.com/AprilRobotics/apriltag.git# 这个不是ros的功能包 2. 编译依赖库apriltag 进入apriltag 文件夹中,然后新建文件夹build mkdirbuild cdbuild cmake ..## 注意两点 ... AprilTag视觉定位系统 热门推荐 明年暑假升初中的博客 2万+ AprilTag是一个视觉基准库，在AR，机器人，相机校准领域广泛使用。通过特定的标志（与二维码相似，但是降低了复杂度以满足实时性要求），可以快速地检测标志，并计算相对位置。 示例图片官网：https://april.eecs.umich.edu/software/apriltag.html列出了如下三篇文章 1. AprilTag: A robust and flexible visu [计算机视觉] 呕心沥血干完AprilTags2原理，全网最完整的AprilTags教程 wangmj_hdu的博客 6704 前言 AprilTag是一个视觉基准系统，类似于二维码，但降低了复杂度以满足实时性需求，AprilTag具有很小的数据有效载荷（4到12位之间）。 AprilTag在非常低的分辨率，不均匀照明，奇怪的旋转或藏在另一个杂乱图像的角落时也可以被自动检测和定位。 它们的设计具有很高的定位精度，我们可以计算相机相对于AprilTag的精确6自由度位姿信息。 可以检测单个图中的多个标签。 可用于多种任务，包括增强现实，机器人和相机校准。 开源项目，官网有丰富的学习资料。 实现原理 自适应阈值 将输入图像（a） 标志识别之AprilTag3_Terry Cao 漕河泾的博客 9-27 在AprilTag3中进行了多项优化,不仅算法更加鲁棒,时间和内存开销大幅减小,更支持了全新格式的二维码。粗看了下,主要做了几点优化:查找矩形前,通过一种新的二值化方法,直接在二值图上查找(这样带来的风险就是二值化失败,矩形形状被破坏... AprilTag详解-Python实现 Magician0619的博客 7752 文章目录一、AprilTag简介二、AprilTag原理三、AprilTag图像生成四、OpenMV实现五、pupil-apriltags六、Python代码实现 一、AprilTag简介 AprilTag是一个视觉基准系统，可用于多种任务，包括增强现实，机器人和相机校准。通过特定的标志（与二维码相似，但是降低了复杂度以满足实时性要求），可以快速地检测标志，并计算相对位置。它可以从普通打印机创建目标，AprilTag检测软件可以计算标签相对于相机的精确3D位置，方向和身份。AprilTag库在C中实现，没有 技术分享 | apriltag_ros的基础讲解 AMOVLAB(阿木实验室) 1389 一 、序言 随着技术的发展，在人工智能、机器人控制的时代。无论是多机协同工作，还是目标识别跟踪。在机器视觉领域，都离不开一个话题，那就是对物体的定位与跟踪。本次介绍的是一个简单而高效的ROS功能包apriltag_ros（apriltag_ros - ROS Wiki）用于实时定位目标的位置和方向。 二 、什么是apriltag apriltag是一个视觉基准库。（AprilTag (umich.edu)）在VR，机器人和摄像机校准等领域有广泛的应用，通过特定的二维码标志，可以快速检测目标位置，. Apriltag使用 u010949023的博客 3843 Apriltag使用 开源项目：https://github.com/AprilRobotics/apriltag apriltag库是一个纯c的库，基本不依赖任何其他库。 Apriltag目前有版本2和版本3，版本3可兼容版本2.版本3的tag如下图： tag2如下： tag3是检测里面四个点，tag2是检测外面四个点。所以同样的大小的tag，tag2的位姿精度会更高。但tag3的检测速度更快(是tag2的两倍以上)。考虑位姿精度，目前我们使用tag2。 我们实际使用4个tag，id分别是tag36h 不同分辨率下Apriltag识别精度测试 TSINGHUAJOKING 1935 §00 背景介绍 在全国大学生智能车竞赛 的智能视觉组 【手拉手 带你准备电赛】April Tag标记跟踪（3D定位）详解 最新发布 weixin_54354252的博客 458 April Tag跟踪检测解析 使用ROS和AprilTags进行相机定位（二维码定位全流程） qq_42879437的博客 6205 使用ROS以及AprilTags进行相机定位，环境配置过程都是参照各路大佬的博客 AprilTag 介绍 04-27 Abstract—Reliable and accurate camera calibration usually requires an expert intuition to reliably constrain all of the parameters in the camera model. Existing toolboxes ask users to capture images of a calibration target in positions of their choosing, after which the maximum-likelihood calibration is computed using all images in a batch optimization. We introduce a new interactive methodology that uses the current calibration state to suggest the position of the target in the next image and to verify that the final model parameters meet the accuracy requirements specified by the user. AprilTags二维码的检测与应用 求真、务实 2893 AprilTags二维码的检测与应用1 AprilTags介绍2 使用python库包apriltag对AprilTag进行检测2.1 python模块apriltag的安装2.2 python模块apriltag的测试用例3 AprilTags二维码检测，以及绘制检测框 1 AprilTags介绍 AprilTag官网：https://april.eecs.umich.edu/software/apriltag 1、AprilTags类似与二维码QR codes（Quick Response Code Apriltag使用之二：方位估计(定位) 8447 Apriltag中计算的Homography 首先，在进行apriltag码检测时，如果检测到会一并计算出图像上apriltag码四个角点对应的homography矩阵，这个homography将这些点映射到到标准的(-1，1),(1,1),(1,-1),(-1,-1)顶点。在上面的示例一中，由homography和apriltag角点为: H = [ 3.3831e-01 7.066e-... 三维重建——AprilTags定位 hehehetanchaow的博客 7134 先附上资料链接： 软件源码：https://github.com/AprilRobotics/apriltags c++:https://github.com/swatbotics/apriltags-cpp ros版的网上很多，就不附链接了。 下面主要针对源码方面记录下自己的使用记录。 环境主要是opencv。 build时候就按照readme里面的步骤来。 $cmake ... 根据Apriltag进行角度和距离检测 TSINGHUAJOKING 2843 §00 背景介绍 Unity3d中使用Apriltag单目测距 zouxin_88的专栏 1265 Hr为二维码高度，单位CM Lr为二维码到相机焦点的距离，单位CM Hv为二维码在照片的高度，单位可为像素，在Unity中transform中的localScale值 Lv为相机的焦距 第一步，求相机焦距 已知： Hr为4.65cm（用卷尺直接测量） Lr为40cm（用卷尺直接测量，起点为摄像头的透镜中心处，差不多就行） Hv为2.276（transform中的localScale值） Lv=Lr*Hv/Hr=19.578494623655 第二步，求真实距离 经过第一步已经求出焦距.. 两个对于Apriltag图片处理问题讨论 TSINGHUAJOKING 532 简 介： ※Apriltag检测是对基于视觉定位的一种比较简便的方法。本文讨论了在apriltag检测结果中的单应矩阵的效果，它与想象中可以直接应用绘制出Apriltag法向量的应用并不符合。对于粘贴在非平面上的Apriltag算法能力进行了测试。如果粘贴在圆柱体上，在一定正对的角度范围内还是可以检测到Apriltag。 关键词： Apriltag #mermaid-svg-ucONLzTjxVtgWM5Y .label{font-family:'trebuchet ms', verdana, aria. Apriltag编解码系统 疯子的博客 936 文章介绍Apriltag的编解码系统，参考文献： AprilTag: A robust and flexible visual fiducial system Edwin Olson University of Michigan [email protected] http://april.eecs.umich.edu 编解码概述 当数据负载从方形中找到的时候，接下来就需要编码系统来判定他是否是可行的，设计编码系统的目标是： ·最大化可区分编码数量 ·最大化可以检测和纠正的位错误数量 ·最小化误报和标签间混 python April tag安装与使用（单应性矩阵） mtfbwy1的博客 444 April tagApril tag安装April tag应用静态图片识别动态中识别利用tag四个角点计算单应性矩阵 April tag安装 在win系统，python安装方法。 April tag应用 静态图片识别 识别图像中tag个数，对其四个角点位置记录。对其后做单应性矩阵计算提供四个点。 #!/usr/bin/env python # coding: UTF-8 # import apriltag import pupil_apriltags as apriltag # for window 旋转的Apriltag码 TSINGHUAJOKING 905 §01 Apriltag定位 Apriltag 可以用于视觉定位基础标识，在AR，机器人，机器视觉领域应用广泛。 ▲ 图1.1 几组Apriltag码 “相关推荐”对你有帮助么？

非常没帮助

没帮助

一般

有帮助

非常有帮助 ©️2022 CSDN 皮肤主题：大白 设计师：CSDN官方博客 返回首页 关于我们 招贤纳士 商务合作 寻求报道

400-660-0108

[email protected]

在线客服 工作时间 8:30-22:00 公安备案号11010502030143 京ICP备19004658号 京网文〔2020〕1039-165号 经营性网站备案信息 北京互联网违法和不良信息举报中心 家长监护 网络110报警服务 中国互联网举报中心 Chrome商店下载 账号管理规范 版权与免责声明 版权申诉 出版物许可证 营业执照 ©1999-2022北京创新乐知网络技术有限公司

躺着中枪ing 码龄7年 暂无认证 15 原创 17万+ 周排名 158万+ 总排名 8万+ 访问

等级 790 积分 31 粉丝 48 获赞 62 评论 342 收藏 勤写标兵 私信 关注 搜博主文章

热门文章 Apriltag原理简介及源代码 38279 cs231n课程作业assignment1（SVM） 9301 分支限界法的0-1背包问题Python实现 6989 cs231n课程作业assignment1（KNN） 5863 pymavlink使用简单教程 5159 分类专栏

mavlink 1篇

cn231n 3篇

中间件技术 4篇

编译原理 1篇

机器视觉 3篇

apriltag 1篇

视觉定位 1篇

Linux内核

大数据 1篇

最新评论 Apriltag原理简介及源代码 KIKU啊: 您好，我使用您的Python代码，发现，它不具备旋转不变性，可以检测出4个角点，但无法分辨tag码的正反方向。

pymavlink使用简单教程 不要一直敲门: 如何用pymavlink 链接硬件的shell呢？

pymavlink使用简单教程 qq_34194064: 博主你好，怎么获取仿真飞控上的航线数据？

Apriltag原理简介及源代码 weixin_44251945: 问一下博主camera position:",Cx, Cy, Cz是相机相对于AprilTag图像上的那一个位置的坐标啊，中间吗？

Apriltag原理简介及源代码 onewhiterabbit: 你好博主，想问一下如何打印位姿信息，代码没有备注有点难找。。。。。谢谢~！

您愿意向朋友推荐“博客详情页”吗？

强烈不推荐

不推荐

一般般

推荐

强烈推荐 最新文章 pymavlink使用简单教程 二分网络上的电影推荐 Linux内核中使用crypto进行sha1方法 2020年1篇2019年3篇2018年1篇2017年6篇2016年4篇

目录 概要 AprilTag视觉定位Python实现 AprilTag过程 AprilTag边缘检测 四边形检测 编码与解码 实现代码

举报

ucoslam 阅读笔记

https://blog.csdn.net/qq_31110769/article/details/121345257

应用场景 & 算法设计

你认为室内SLAM与自动驾驶SLAM有什么区别？

这是个开放题，参考无人驾驶技术与SLAM的契合点在哪里，有什么理由能够让SLAM成为无人驾驶的关键技术？

答： 都属于SLAM的问题范围。但应用场景不同，技术上的侧重点也不同。

无人驾驶技术与SLAM的契合点在哪里？

SLAM传统上还是面向室内等缺少GPS信号的应用，例如室内移动机器人导航，而在无人驾驶汽车上，它的意义和作用是什么，已经有高精度的地图和城市GPS信号了，那就是说SLAM只是为了感知么？

最初，SLAM的提出就是为了解决未知环境下移动机器人的定位和建图的问题。所以，笼统的说，SLAM对于无人驾驶的意义就是如何帮助车辆 \感知** 周围环境，更好的完成导航、避障、路径规划等高级任务。 现在已经有高精度的地图，暂且不去考虑这个地图的形式、存储规模和如何用它的问题。首先，这个构建好的地图真的能帮助无人驾驶完成避障或者路径规划等的类似任务吗？至少环境是动态的，道路哪里有一辆车，什么时候会出现一个行人，这些都是不确定的。所以从实时感知周围环境这个角度来讲，提前构建好的地图是不能解决这个问题的。

另外，GPS的定位方式是被动的、依赖信号源的，这一点使得其在一些特殊场景下是不可靠的，比如城市环境中GPS信号被遮挡，野外环境信号很弱，还有无人作战车辆作战中信号被干扰以及被监测等。 所以像视觉SLAM这种主动的并且无源的工作方式在上述场景中是有优势的。从硬件角度讲，目前主流的视觉SLAM方案，在构建低成本，小型化，易于搭载的硬件平台方面也是有优势的。

有什么理由能够让SLAM成为无人驾驶的关键技术？

1.我个人不是很赞同这个逻辑。SLAM作为一个很庞杂的系统，其本身也有很多关键环节和实际应用中会遇到的难题，作为一种应用场景越来越广泛的技术（如自动机器人，无人机，无人驾驶，AR），它可能永远不会成为无人驾驶的关键技术，与其思考这个问题，不如关注SLAM本身，即围绕定位和建图这两个基本任务，来想想

• 里程计是不是可以估计的更准确，
• 环境地图信息是不是可以建立得更丰富（比如有用的语义信息），
• 场景识别/闭环检测是不是能保证更高的准确率和召回率，
• 是不是可以借助其他传感器完善SLAM系统，

接下来在想想SLAM能帮助无人驾驶做些什么？只有技术越来越完善和成熟，才能被应用到更多的实际场景中。

2.我想SLAM真正能发挥作用的区域是last mile或者一些高精度地图覆盖不到的非结构化环境。

机器人从超市门口出发，前往3公里外的小区送货。请你设计一个定位系统，包括传感器的配置、算法的流程，用伪代码写出来

给定几个连续帧的带有位姿的帧，如何去测量车道线相对于世界坐标系的坐标。

其他

CAN通讯

ROS操作系统

自主导航的实现原理

参考

SLAM、定位、建图求职分享

2022最新SLAM面试题汇总（持续更新中） - 知乎 (zhihu.com)

SLAM常见面试题（一） - 知乎 (zhihu.com)

SLAM常见面试题（二） - 知乎 (zhihu.com)

SLAM常见面试题（三） - 知乎 (zhihu.com)

(2 封私信 / 35 条消息) 小马恺文 - 知乎 (zhihu.com)

(9条消息) SLAM_视觉SLAM面试题及答案汇总_惊鸿一博的博客-CSDN博客_slam面试题

（文章转载至深蓝学院学员总结-彭季超）+ 自己补充

slam特征点深度 svd_【干货】视觉SLAM面试题汇总（第二部分）

视觉SLAM面试题汇总（2019年秋招题库参考）——第一部分

万字干货！视觉SLAM面试题汇总（19年秋招）第二部分 26~51

3D VISION、SLAM求职宝典 | SLAM知识篇（D1，重点 ）

电子书籍

update