Open Set Domain Adaptation 开集领域适应
1. Motivation
2017年ICCV上发表了一篇题为 O p e n S e t D o m a i n A d a p t a t i o n Open Set Domain Adaptation OpenSetDomainAdaptation[1]的论文说:一般我们所讲的领域适应(domain adaptation)是在一个闭集(close set)的前提条件下进行的,即源域和目标与拥有相同的标签类别。但是在大多数的实际情况中,源域和目标域可能只共享了一部分相同类别。如图1所示(图片来源于文献[1]),在Close set domain adaptation问题中,目标与中出现的标签类别全在源域中出现了,而在Open set domain adaptation问题中,目标域中出现的摩托车、电视、飞机等均未在源域中出现;相反,源域中出现的鸟、笔记本、杯子也未在目标域中出现。
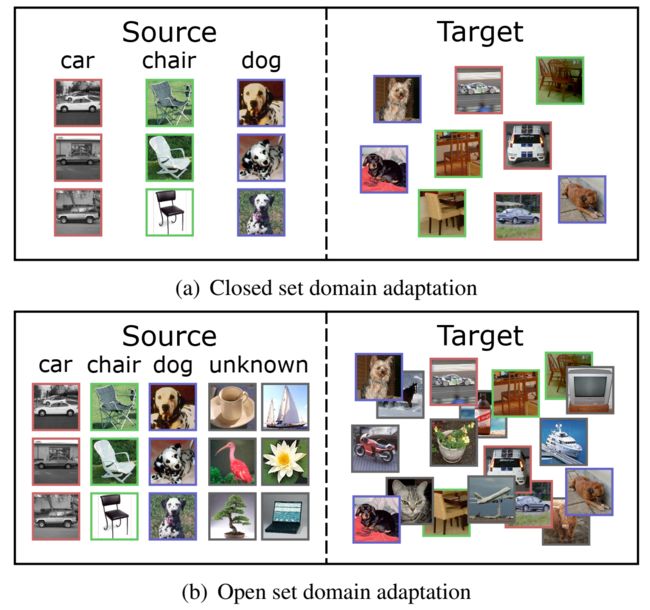
显然domain adaptation in close set中的方法不能用于解决domain adaptation in open set问题,在进行特征对齐的时候只能对其已知的类别,不能对齐未知的类别。
随后,在2018年ECCV上有一篇论文Open Set Domain Adaptation by Backpropagation,对Open-set domain adaptation进行了重新定义,
2. Method
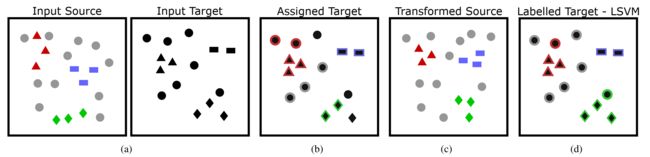
为解决Open Set问题,作者提出了Open Set Domain Adaptation方法,步骤如下:
( a ) 源域中包含已知带标签的样本(分别用红、蓝、绿以及不同形状表示)和未知样本(灰色表示),而目标域中不包含任何标签信息;
( b ) 首先,我们为一些目标样本分配类别标签,留下未标记的异常样本;
( c ) 通过减小标记为同一类别的源域和目标域数据之间的距离,我们可以学习到从源域到目标域的映射关系。将( b )和( c )反复迭代,直到源域与目标域之间的距离收敛到局部最小值;
( d ) 为了个目标域的样本打上标签(红色,绿色,蓝色和灰色(未知类别)),我们在已经映射到目标域的源域数据上学习分类器,并用它来分类目标域样本。
####2.1 Unsupervised Domain Adaptation
源域数据: C C C个类别,其中 ∣ C − 1 ∣ \left | C-1\right | ∣C−1∣个已知,1个未知
目标域数据: T = { T 1 , T 2 , . . . , T T } \mathcal{T}=\left \{T_1, T_2, ...,T_{\mathcal{T}}\right \} T={T1,T2,...,TT}
目标:给目标域中的每一个数据 T \mathcal{T} T打上标签 c ∈ C c \in C c∈C
损失函数:将目标域样本 T t T_t Tt标记为标签 c c c的损失函数记为: d c t = ∥ S c − T t ∥ 2 2 d_{ct}=\left \| S_{c}-T_{t}\right \|_{2}^{2} dct=∥Sc−Tt∥22,其中 T t T_{t} Tt是目标域样本t的特征表达, S c S_{c} Sc是源域中标签为 c c c的样本的均值。这里采用的是样本一阶矩来度量两个分布间差异,当然我们是希望 d c t d_{ct} dct越小越好,表明给目标域数据 T c T_{c} Tc的标签越接近真实标签。
为了增加模型的鲁棒性,这里并不会为目标域中的没有一个样本都分配一个标签 c c c,而是引入了异常值 o t o_{t} ot,整个模型的优化目标如下:
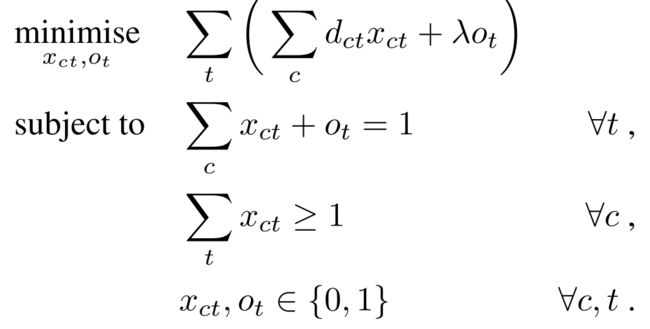
其中 x c t x_{ct} xct和 o t o_{t} ot是两个二值变量,他们要么是0要么是1。当 x c t x_{ct} xct为0 , o t o_{t} ot为1表明目标域中的该样本为异常值,反之亦然。第二个约束条件确保至少有一个样本被标记为了标签 c c c。所以最终的目标是确保目标域中所有样本的 d c t d_{ct} dct与 o t o_{t} ot的和最小。
2.2 Semi-supervised Domain Adaptation
当目标域有一小部分标记数据之后无监督问题可以变成一个半监督问题。要处理semi-supervised情况,只需要在现有的unsupervised情况下,添加那些有label的target的约束信息。作者为了达到这个目的,引入了一个新的变量 x c ^ t t = 1 , ∀ ( t , c ^ t ) ∈ L x_{\hat{c}_{t}t} = 1,\forall (t,\hat{c}_{t})\in \mathcal{L} xc^tt=1,∀(t,c^t)∈L,其中 L \mathcal{L} L表示带目标域带标签样本集, c ^ t \hat{c}_{t} c^t表示目标域样本 t t t的标签。该项表示所有已有标签的目标域样本不改变其标签。目标函数就变成了:

其中, d c c ′ = ∥ S c − S c ′ ∥ 2 2 d_{cc'}=\left \| S_{c}-S_{c'}\right \|_{2}^{2} dcc′=∥Sc−Sc′∥22,它表示当样本 t t t的临近点 中有临近点 N t N_{t} Nt被分配到另一类的时候,额外加上一个类间的距离差作为损失。
2.3 Mapping
我们假设有一个线性变换,可以估计出源域到目标域的映射关系,用一个矩阵 W ∈ R D × D W \in \mathbb{R}^{D \times D} W∈RD×D。损失函数如下:
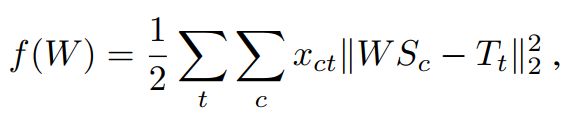
对 W W W求偏导可以求出使 f ( W ) f(W) f(W)最小的 W W W。
本文原载于我的简书
References:
[1] Busto, P. P. , and J. Gall . “Open Set Domain Adaptation.” IEEE International Conference on Computer Vision IEEE, 2017.
[2] 《小王爱迁移》系列之九:开放集迁移学习(Open Set)